Aritalab:Lecture/NetworkBiology/Network

学習事項

• グラフの定義
• 生物学と数学／情報科学ではネットワークの取り扱いが異なる
  • 生物学では推移律が成立しない関係をネットワークで取り扱い（相同性など）、その結果を実体に敷衍して解釈する（例えば進化など）
  • 数学／情報科学ではネットワークという構造そのものを研究対象とする
• 生物学では、ネットワークの中で「有意な」（生物学的に面白い）頂点を探す研究が多い

ネットワークとはなにか

グラフ理論では、ネットワークのことをグラフと呼びます。正確なグラフの定義は以下のようになります。

頂点の集合 V と辺の集合 E の間に f : E → V × V という関係を導入した構造 G := ( f , V, E)

辺は頂点を 1 対 1 で結ぶ関係であることに注意してください。多対多を結ぶ辺をもつグラフはハイパーグラフと呼ばれ、Berge などが研究対象にした時期もありましたが、理論的な解析は難しいようです。一般に、グラフ理論では辺や点に数値を割り振ることはおこないません。 頂点に接続する辺の数を次数 (degree) といいます。

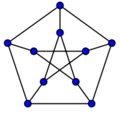
K₅完全グラフ 

頂点数 5 で、各頂点が他の全頂点と結ばれたグラフです。いわゆる星形の周りを辺で囲んだ形になります。どの頂点も次数が 4 で、辺を交差させること無く平面に描けないという特徴を持ちます（非平面グラフ）。

K_3,3完全二部グラフ 

頂点数 3 のセット二組の間でのみ、全頂点間に辺があるグラフです。どの頂点も次数は 3 で、非平面グラフです。

計算機科学では、辺に流量などの重みをつけたとき、グラフではなくネットワークと呼ぶことが多くあります。これはオペレーションズリサーチにおいて流量計画問題などが盛んにおこなわれたことと関係するようです。一般には、流量やコストなど整数や実数を辺に割り振ります。

残念なことに、生物学ではネットワークに対する正確な定義はありません。実際の物理化学現象とは関係のないネットワークも研究されることがあります。

生物学におけるネットワークの例

• 代謝・シグナル伝達のネットワーク
• 遺伝子相同性のネットワーク
• タンパク質内の近接原子ネットワーク

社会学におけるネットワークの例

• 電話やSNSの友達ネットワーク
• 会話のネットワーク（時間情報あり）
• コミュニティや役職のネットワーク

演習問題

Petersen graph の点彩色数が 3 であることを確認しよう。辺彩色数が 4 であることも確認しよう。

完全二部グラフ K3,3 が平面に描けないことを確認しよう