Aritalab:Lecture/NetworkBiology/Markov Chains/StationaryDistribution
Contents |
再帰時間の母関数
再帰時間と初再帰時間の間には以下の関係が成立します。
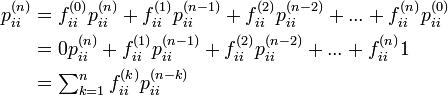
初通過時間も同様にあらわせます。
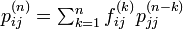
関数 fij と pij の母関数をそれぞれ Fij(s) と Pij(s) であらわします[1]。
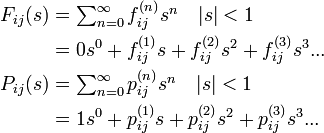
(−1, 1) の間に収束する二つの数列の積はやはり(−1, 1) の間に収束することが知られています (Wade 2000)。
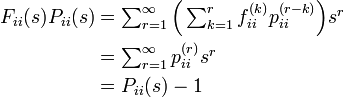
Pii(s) から 1 を引くのは Fii(s) Pii(s) の第一項が 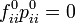 であるのに対し Pii(s) の第一項は 1 になるからです。この関係から以下が導かれます。
であるのに対し Pii(s) の第一項は 1 になるからです。この関係から以下が導かれます。
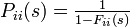
同じようにして、通過時間の母関数に対して
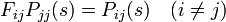
が成立します。こちらは Pij(s) から 1 を引きません。これは Pij(s) の第一項が 1 でなく 0 であることに由来します。
Abel の収束定理
以下の定理 (Abelの定理) は証明せずに利用します。この定理と母関数の関係から、再帰性を 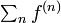 ではなく
ではなく 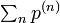 で議論できるようになり、再帰性の計算を楽にします。
で議論できるようになり、再帰性の計算を楽にします。
- もし
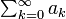 が収束する場合、
が収束する場合、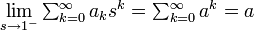
- もし
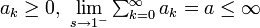 の場合、
の場合、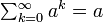
- 定理: 状態 i が再帰確実(不確実)であることと
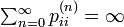 は同義
は同義
状態 i が再帰確実と仮定します。すなわち
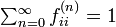
このときAbelの定理から
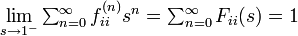
母関数の関係 P(s) = 1/(1 - F(s)) を用いると
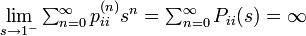
したがって再びAbelの定理から 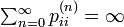 となります。
となります。
逆方向は背理法で示します。 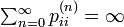 のときに状態 i が再帰不確実 (transient) と仮定します。このときAbelの定理から
のときに状態 i が再帰不確実 (transient) と仮定します。このときAbelの定理から
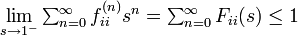
母関数の関係 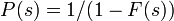 を用いると
を用いると
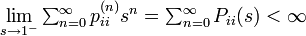
これは 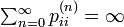 と矛盾するので定理が証明できました。
と矛盾するので定理が証明できました。
- 補題:同じ同値類に属する状態は、再帰性に関する性質が等しい
状態 i, j が同じ同値類に属すと仮定し、m,n ステップでそれぞれ i → j, j → i の遷移が可能とします。すなわち 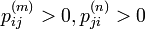 です。
です。
状態 i が再帰確実 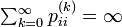 と仮定します。状態 j について以下が成立するので、j もやはり再帰確実です。
と仮定します。状態 j について以下が成立するので、j もやはり再帰確実です。
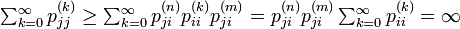
状態 i が再帰確実でなければ、i は不確実です。そのため同じ同値類に属す状態集合は、全て再帰確実か、すべて不確実のどちらかです。
定常分布の極限定理
以下の定理の証明はいずれもKarlin & Tayler (1975) を参照してください。
- 定理:既約、再帰確実、非周期的なマルコフ連鎖は以下を満たす
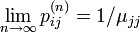
ここで 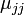 は状態 j の平均再帰時間です。i の値に関係ない (j に依存する)値に収束する点に注意します。
は状態 j の平均再帰時間です。i の値に関係ない (j に依存する)値に収束する点に注意します。
- 定理:既約、再帰確実、周期 d のマルコフ連鎖は以下を満たす
周期 d を持つ場合、d の倍数にあたる遷移の時だけ
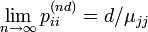
それ以外は 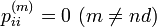 になります。
になります。
状態 i が有限再帰な場合は 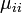 が有限の値ですが、ゼロ再帰な場合は無限大、つまり
が有限の値ですが、ゼロ再帰な場合は無限大、つまり 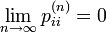 になります。
になります。
- 定理:規約、有限再帰、非周期的なマルコフ連鎖は、定常分布
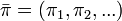 をただ一つ持つ
をただ一つ持つ
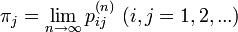
マルコフ連鎖自体は有限でなくても良い点に注意しましょう。定常分布をただ一つ持つような条件を、エルゴード的と呼びます。 状態 i がエルゴード的な時、i は有限再帰、非周期的です。マルコフ連鎖がエルゴード的になるには、全ての状態がエルゴード的かつ規約でなくてはなりません。このとき、確率行列は以下を満たします。
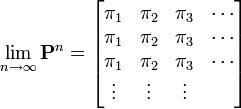
つまり初期値に依存しない値になります。上の定理とあわせると、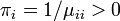 が導かれます。
が導かれます。
マルコフ連鎖の分類
マルコフ連鎖は以下のように分類できます。
- 既約 or 非既約
- 再帰不確実 or ゼロ再帰 or 有限再帰
- 周期的 or 非周期的
連鎖の有限性とゼロ再帰性
ゼロ再帰性は、有限マルコフ連鎖では生じません。
- 定理:有限のマルコフ連鎖における状態は再帰不確実か有限再帰(ゼロ再帰的な状態は無い)。また、全ての状態が再帰不確実になることもない
まず全ての状態が再帰不確実である場合を考えます。無限時間後の移動先は確率行列を無限回かけると求められますが、再帰不確実な場合は、全ての状態において遷移確率がゼロに近づいていくはずです。
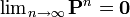
これは P が確率行列であることと矛盾します。
次にゼロ再帰性について考えます。マルコフ連鎖は有限なので、ゼロ再帰的な状態が属す、有限サイズの同値類 C が存在します。この同値類に対応する確率行列(Pの部分行列)P' を考えると、ゼロ再帰性から C に属す状態の遷移確率もゼロに近づいていくはずです。
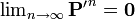
しかし C に対応する部分行列は再帰的ですから確率行列でもあるので、矛盾します。
つまり、ゼロ再帰的な状態と再帰不確実な状態はいずれも 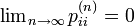 を満たすので有限の状態数で再帰性を満たせないというわけです。
を満たすので有限の状態数で再帰性を満たせないというわけです。
- 定理:有限のマルコフ連鎖に含まれる同値類は、閉じているなら有限再帰
有限再帰な状態集合は必ず閉じています。なぜなら閉じていない場合は、いずれかの状態 i において j → j という集合外への遷移が存在し、状態 i の再帰確率はこの遷移確率 pij ぶん 1 より少なくなるからです。これは再帰的であることの定義に反します。
閉じた同値類が有限再帰でない、つまり再帰不確実であると仮定します(ゼロ再帰ではありえない)。すると同値類に含まれる状態全てが再帰不確実のはずです。しかし全てが再帰不確実の場合、同値類の中から集合外への遷移が無くてはなりません。これは閉じていることと矛盾します。
正規行列
マルコフ連鎖の世界では、全ての要素が pij > 0 となる確率行列を 正規行列 (regular matrix) と呼ぶことがあります。確率行列が正規な場合、マルコフ連鎖は規約で非周期的(全ての状態間を行き来できる)です。このため正規な確率行列を持つマルコフ連鎖は、有限再帰的でもあります。
ペロン・フロベニウスの定理によると、非負の行列 P が既約であれば
- 最大固有値は正で、かつ、実数 ( 1 が最大固有値)
- 最大固有値は、Aの固有方程式の単純根 (定常分布はただ一つであることに対応)
- 最大固有値に対応する固有ベクトルの成分は、全て正か又は全て負 (当然だが、定常分布は全て正)
が成立します。つまり最大固有値 1 がただ一つの定常分布に対応するためには、確率行列 P は正規(既約かつ非周期的)でなくてよく、規約なだけで十分です。非周期性は、唯一の定常分布に収束するために必要な条件となります。
- 補足
- ↑ fij と pijは一時的 (transient) かもしれないため総和は 1 以下の可能性があります。したがって確率母関数にはなっていません。