Aritalab:Lecture/NetworkBiology/Game

ネットワーク上のゲーム

各頂点は 協力 (C: Cooperate) か裏切り (D: Defect) のいずれかの戦略を取るとする。 協力者は隣接頂点それぞれにコスト (cost) c を支払い、隣接する頂点は利得 (benefit) b を受け取る。 裏切る場合はコストを払わず、隣からの利得のみを受け取る。 頂点の適応度 (fitness) を支払いと利得の合計で判断し、戦略を更新する方法として以下の2通りを考えよう。

1. 出生死亡過程: 単位時間毎に適応度に応じて頂点を選択し、隣接頂点をランダムに選んで同じ戦略へとコピーする。
2. 死亡出生過程: 単位時間毎に頂点がランダムに選ばれて死亡する。隣接する頂点がそれぞれの適応度に応じて自分の戦略をその頂点にコピーする。

一次元格子

もっとも単純なケースとして単純サイクルを考える。

出生死亡過程の場合

C戦略とD戦略をとる頂点の境界部分にある2頂点を考慮すればよい。

$\begin{matrix} \longleftrightarrow & \circledcirc & \longleftrightarrow & \circledcirc & \longleftrightarrow & \circledast & \longleftrightarrow & \circledast & \longleftrightarrow\\ & & & -2c + b & & b & & & \end{matrix}$

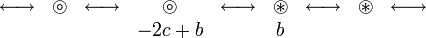
C戦略の端にいる頂点は、隣接する2頂点分のコストを払って利得を片側からしか得ないので合計は b − 2c になるが、D戦略の端にいる頂点は利得 b を得られるので、いかなる b, c であってもD戦略が優位になる。

死亡出生過程の場合

C戦略とD戦略をとる頂点の境界部分から2つ離れたところまでの合計4頂点を考慮する。

$\begin{matrix} \longleftrightarrow & \circledcirc & \longleftrightarrow & \circledcirc & \longleftrightarrow & \circledast & \longleftrightarrow & \circledast & \longleftrightarrow\\ & 2(b - c) & & -2c + b & & b & & 0 & \end{matrix}$

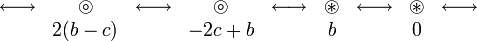
C戦略を取る側は、D戦略と隣接する頂点が b − 2 c、そのまた隣は 2(b − c)になる。 D戦略を取る側は、C戦略と隣接する頂点が b、そのまた隣は 0 になる。

従って b / c > 2 の場合はC戦略が優位。 一般化すると、次数 k の格子であれば 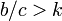$b/c > k$の場合にC戦略が優位になる。