Aritalab:Lecture/Biochem/ProteinStructure
|
タンパク質の構造
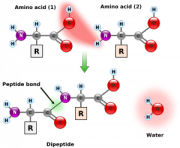
タンパク質は20種類のアミノ酸から構成され、アミノ酸どうしはアミノ基とカルボキシル基の間にペプチド結合を形成します。 この結合は共鳴によって二重結合性を帯びるので平面構造をとります。 Cα(アミノ酸の中心炭素)の間に炭素と窒素が1個ずつ入りますが、平面が固定されるのでCα-N結合角(φ ファイ)とCα-C結合角は(ψ プサイ)の二結合ぶんで立体配置を決定できます。
二面角
アミノ酸の中心に位置する炭素 (Cα) に注目すると、側鎖の他にそれぞれがペプチド結合に関わる -C(=O)- と -N(H)- が接続しています。 ペプチド結合は平面構造をとりますが、それぞれが -C-Cα 軸と Cα-N- 軸を中心に回転できます。 その回転角度 φ, ψ は ±180 ° の間をとることができ、二面角と呼ばれます[1]。
一次構造
ペプチド結合によって連結されたアミノ酸の配列を一次構造といいます。コドンの並び順で最初にくるアミノ酸側がアミノ基末端 (N末端)、最後のアミノ酸側がカルボキシル末端 (C末端) となります。
代表的な一次構造のデータベースには以下のものがあります。いずれも特徴的なアミノ酸配列という形式で機能や構造を表現しています。
二次構造
タンパク質のドメインは、二次構造という単位で理解されます。二次構造は水素結合や分子間力で構成されるため、加熱や pH、尿素などの変性剤、界面活性剤などで変化します。
水素結合のエネルギーは、1結合あたり 2 ∼ 10 kcal/mol と見積もられており、共有結合と比較すると 1/10 以下になります。
| α-へリックス (H) | β-シート (E) | ループ、ターン (C) |
|---|---|---|

(画像はCATHより) |

|

|
| アミノ酸が平均3.6残基で右巻きにらせんを巻いた構造です。(左巻きもありますが、数は少なくなります。)
n 番目のアミノ酸におけるペプチド結合の -C(=O)- 部分が、n + 4 番目のアミノ酸におけるペプチド結合の -N(H)- と水素結合して形成されます。この一般系を 4-α へリックスと呼びます。 このほか 3 アミノ酸、5 アミノ酸で一周する構造もあり、それぞれ 310 へリックス、π へリックスと呼ばれます。 グリシンやプロリンをあまり含みません(らせんを妨げる)。電荷を持つアミノ酸や大きなアミノ酸も比較的少ないです。 |
伸長したアミノ酸が並行に並んだストランド構造です。
シートの間で-C(=O)- 部分が -N(H)- と水素結合して形成されます。 ストランドが同じ向きに並んだ場合を並行 β シート、互い違いに並んだ場合を逆並行 β シートといいます。イソロイシンやバリンのような疎水性残基が使われます。多くは親水性の側と疎水性の側を作ります。 |
α-へリックスやβ-シートは、特定の構造をとるループや、構造が不定のディスオーダー領域で連結されます。細胞外にある多くのタンパク質では、硫黄を含むシステインどうし間にS-S架橋をつくったジスルフィド結合が立体構造を安定化させます[2]。急な角度を形成するためにグリシンやプロリンが多くなります。 |
二次構造の分布
二次構造を H, E, C の3種に分けるとそれぞれ 30, 20, 50% の割合になります。二次構造の予測ツールとして常に C と予測するプログラムを作成したら正解率は 50 % です。この正解率を上げるのは簡単にみえて難しく、予測率が 70 % を初めて超えたのは 1993年 B. Rost による予測法でした。70%を超えたことを論文タイトルにした位です。[3] 現在でも予測率は 80 % 程度で、配列アライメントに基づくツールがよく使われています。
予測法
初期
- Chou-Fasman 法 [4]
- 各アミノ酸について H, E, C の中での存在比を求めます。そして H らしいアミノ酸が続く部分を ヘリックスと予測する方法です。例えばグリシンが多いから C、のように予測します。
- Garnier-Osguthorpe-Robson 法 [5]
- 17アミノ酸残基のウィンドウを利用し、各アミノ酸の左右8残基の位置にくるアミノ酸の存在比を利用します。(ヘリックスなら左右4, 8 番目のアミノ酸が同じ側に来るので17残基をとります。)H, E, C のクラス毎に 20 x 17 パラメータを用意して存在比を求めなくてはなりません。
配列類似性を用いたもの
その後、ニューラルネットワーク (NN) を用いた予測法が大流行します。NN は17 や 13 といったウィンドウ幅のアミノ酸残基に対応するセルをもち、それらのセルが中間レイヤを介して H, E, C のいずれかを支持します。この手法は、NN を例題によってトレーニングしておき、その結果を用いて予測する方法であることから配列のローカルな類似性を用いた予測といえます。
結論として、これらの手法(初期のものを含む)で予測率 70 % を達成することはできませんでした。ホモロジー検索によって近縁の配列をデータベースから集め、そのマルチプルアライメント結果(プロファイル)を NN で学習させる手法になって初めて 70 % を超えるようになりました。[6] この70%超えを達成したのが B. Rost という人です。この仕事で博士号を取得し、今は国際計算生物学会 (ISCB) の会長をしています。
進化的情報の利用
二次構造の予測には今もニューラルネットワークや隠れマルコフモデルが使われます。ただし、ニューラルネットワークが特にこの問題に適しているわけではありません。おそらくSVM などの他手法でも同様の精度は達成できるでしょう。歴史とともに精度が向上するのは主に psi-BLAST など配列アライメント(プロファイル)の性能が上がったことに依拠します。
いまのところ予測ツールではInterProScan がよく知られています。これは既存のツール 10 種以上による予測結果をまとめてE-mailで返してくれるシステムで、メタツールと呼ばれます。メタツールの登場により、 80 % 程度の精度で二次構造が予測できると考えられています。
予測の限界
今後、より多くの情報が集まったら二次構造は完全に予測できるのでしょうか。現在はそう考えられていません。 まず、タンパク質の立体構造から二次構造への変換が必ずしも一意ではありません。有名な二次構造データベースにDSSPやSTRIDEがありますが、両者でも二次構造の割り当ては異なっています。結局、立体構造をきちんと予測できなければ二次構造の予測精度も80~85%から上がらないだろうというのが大方の見解です。これをうけて、最近は特定の部分構造(例えば、ディスオーダー領域と呼ばれる構造不定部分や特徴的なターン構造)を予測する方向に研究の興味が移っています。
三次構造
いわゆるタンパク質の立体構造を三次構造といい、原子の座標であらわします。三次構造の形成にはアミノ酸側鎖どうしの疎水結合力が大きな役割を果たします。特に球状のタンパク質では疎水性アミノ酸がコアを形成し、親水性アミノ酸が分子表面に分布します。
ファミリーという概念
タンパク質の立体構造を表現するのにしばしば
- クラス ... all-α や all-β といった大まかなドメイン構造
- フォールド ... globin-like のように特定のタンパクを例にした類似構造
- スーパーファミリー ... フォールドから示唆される、共通祖先を持つタンパク質群
- ファミリー ... 相同タンパク質の集まり
という階層が用いられます。上から順に細分化されるツリー構造をなしますが、クラスとフォールドが構造上の類似性だけから判断されるのに対し、スーパーファミリーは進化上、同一系統のタンパク質グループに与えられる名称です。BLAST等の相同性検索で見つかるものをファミリーと呼びます。
データベース
Protein Data Bank (PDB) は代表的な立体構造のデータベースで、およそ 10 万のタンパク質構造が登録されています。タンパク質の特徴や歴史を記した「今月の分子」は大変勉強になるのでぜひ覗いてみてください。 正確な立体構造はX線結晶解析やNMRで決定するしかありませんが、進化の観点から、構造既知の配列に似ている配列は、立体構造も似ていると仮定できます。面白いことに、タンパク質の立体構造は配列以上に保存されている場合が多いのです。
| アミノ酸の保存率 | 検出できる代表的ソフトウェア | 進化的な考察 |
|---|---|---|
| 30% 以上 | 殆どの配列解析ソフト | 9割以上が同一祖先由来でホモロジー(相同性)を持ちます。 |
| 25%近辺 | Blast (E-value 10-4) | トワイライトゾーン。配列解析ソフトの限界。アミノ酸保存率が25%以下の場合、相同である確率は10%以下に下がるという論文もあります。[7] |
| 20%以下 | PSI-Blast (E-value 10-4) | 相同性の確認には立体構造比較が必須。 |
立体構造予測
Ab initio 予測
原子間にポテンシャルエネルギー関数を導入して、エネルギー最低の状態を最適化問題として解く手法です。エネルギー関数はニュートン力学を用いていて量子力学は使いません。最適化部分をどのアプローチで行うかにより、呼び方が異なります。
- 分子力学 (molecular mechanics) 空間内をエネルギーが低くなるほうに動かす、いわば山登り的最適化です。
- 分子動力学法 (molecular dynamics) ニュートンの運動方程式によって原子を動かします。
- Monte-Carlo法 原子の動きをランダムに決定します。
最近の主流は D Baker のRosetta法に代表される、フラグメントアセンブリー・モンテカルロ法です。フラグメントアセンブリー法では、与えられたタンパク質をまずウィンドウ幅 9 残基程度のフラグメントにずらしながら分解します。各フラグメントについて PDB など立体構造データベース内を検索して既知のタンパク質における折り畳み方をリストアップしておきます(ライブラリと呼びます)。その後、与えられたタンパク質の構造をランダムにフラグメント単位でライブラリ内のものと交換し、よりよい構造を探索していく方法です。Baker らのグループは最近 Fold It! というコミュニティ参加型のゲームとして、エイズタンパク質の構造を解いたことで世界中に報道されました。(研究者の間ではもともと有名。)
ホモロジーモデリング
タンパク質の立体構造は配列よりも保存されやすいことを利用し、配列が似ているなら構造も同じと考えて予測する手法です。まず BLAST や 立体構造用に開発されたスレッディング法と呼ばれるもので PDB などのデータベース中の類似タンパク質を探します。次に、Modeller などのソフトウェアでテンプレートとなる立体構造の中に与えられた配列を埋め込みます。
ここで使うスレッディング法の代表格が、Eisenbergらが開発した 3D-1D と呼ばれる手法です。その名前は立体構造 (3D) とアミノ酸配列 (1D) のアライメントを求めることに由来しています。基本はアミノ酸インデクスに同じ(タンパク質参照)で、各アミノ酸に対して立体構造上の二次構造(α, β, coil) と埋もれやすさ(溶媒に接する、半分埋もれている[極性・わずかな極性]、埋もれている[極性・わずかな極性・疎水性])のスコアを設定することで、動的計画法による配列と立体構造のアライメントを可能にしました。3D-1Dスコアの設定は、立体構造を与えられた時にその構造を最も取りやすいアミノ酸配列を求めることに相当するので、逆フォールディング問題とも呼ばれます。
四次構造
複数のタンパク質サブユニットの空間配置を四次構造といいます。
- ↑
タンパク質の構造を表現する二面角に対するギリシャ文字は常に
- アミノ基側の結合がファイ φ ... C(i-1)−N(i)−Cα(i)−C(i)
- カルボキシル基側の結合がプサイ ψ ... N(i)−Cα(i)−C(i)−N(i+1)
- ↑ 細胞内のタンパク質はS-S架橋をほとんど作りません。
- ↑ Rost B, Sander C "Prediction of protein secondary structure at better than 70%" J Mol Biol 1993; 232:584 B. Rost はこの仕事で学位を取り、2012年現在は国際学会ISCBの会長も務めています。
- ↑ Chou P, Fasman G "Prediction of protein conformation" Biopolymers 1974; 13:211
- ↑ Garnier J, Osguthorpe D, Robson B "Analysis and implications of simple methods for predicting the secondary structure of globular proteins" J Mol Biol 1978; 120:97
- ↑ Rost B, Sander C (1993) "Prediction of protein secondary structure at better than 70%" J Mol Biol 232:584
- ↑ Rost B (1999) Protein Eng 12(2):85-94