Aritalab:Lecture/Basic/Distribution
| Menu: | 確率の定義 | 平均と分散 | 分布 |
Contents |
正規分布
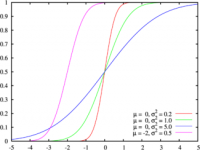
よく見る釣鐘型の連続的な分布です。どんな分布であれ、その中から要素をランダムに抽出して和をとったものの分布は、正規分布に近づくという性質があります(中心極限定理)。期待値が0, 分散が1になるようにスケーリングしたものを標準正規分布といい、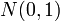 と書きます。正規分布はガウス分布とも呼ばれます。
と書きます。正規分布はガウス分布とも呼ばれます。
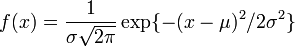
ここで σ は標準偏差、 μ は平均を表します。正規分布は同じ作業を繰り返し行った際によく見られます。また血清中のアルブミン量や、身長、体重なども正規分布に従います。
正規分布表
標準正規分布表の見方を説明しましょう。
|
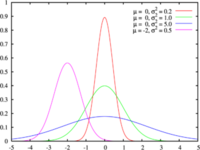 (図はWikipedia 正規分布より) (図はWikipedia 正規分布より)
|
表における z の値は上から順に左 → 右方向にみます。値がだんだん小さくなっている点に注意してください。これらの値は、正規分布全体の面積を 1.0 としたときの、 z から上側の面積を示しています。例えば標準偏差が 2.0 以上の面積は 0.0228、2.2 以上の面積は0.0139 になります。
この表から
- 平均の ±1 σ 内に入る量 68% (1 - 0.1587*2)
- 平均の ±2 σ 内に入る量 95% (1 - 0.0228*2)
- 平均の ±3 σ 内に入る量 99.7% (1 - 0.0013*2)
であることがわかります。
z 値と累積分布関数
正規分布に従う確率変数の値は、平均と分散の値を用いて規格化することにより z 値 を求められます。
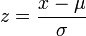
ある z 値以下の面積を与える関数を累積分布関数 (cumulative distribution function) といい、F(z) と書きます。 標準正規分布表から、F(2) = 0.9772, F(-2) = 0.0228 です。
対数正規分布
対数 (logarithm) を取ると正規分布に従うものを対数正規分布 (log-normal distribution) と呼びます。血清中の抗体量や、液体を噴霧して得られる液滴サイズが対数正規分布に従うことが知られています。正規分布から逆対数をとれば得られるので、正規分布と同様に扱えます。
二項分布
コイン投げをして表裏がでる回数を記録したときにできる分布です。離散的な分布ですが、回数が多くなると (30程度) 正規分布で非常によく近似できることが知られています。
ポアソン分布
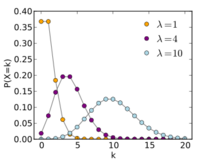
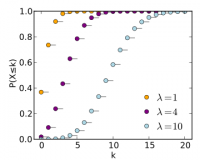
稀にしか起こらない離散的な事象を数える際に用いる分布です。 単位時間中に平均 λ 回発生する事象が、ぴったり k 回発生する確率を
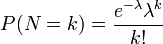
と定義します。