Aritalab:Lecture/Algorithm/GraphNormalization

グラフ構造の正規化

化学構造をデータベース化する際に、構造が同じであるかどうかが迅速に検出できると便利です。例えば新しい構造があるとき、データベース中に既に登録されているかをどう調べればよいでしょう。一般的には化学構造を適切なルールに従って比較しやすい標準形にします。この標準化プロセスを正規化(canonicalizationまたはnormalization)といいます。

計算機で構造を処理する場合、構造を文字列で書き下せると便利です。この文字列はいってみれば構造の「名前」を生成することと等価なので、unique nameなどと呼ばれることもあります。

基準番号付けによる正規化

MOLフォーマットやSMILESフォーマットは原子を書く順番が任意のため、そのままでは構造の比較は困難です。そこで原子に１から順に基準番号を振り、構造の同一性を番号順に調べればよいというアイデアを思いつきます。（ただし対称な構造を持つ場合は、番号が一意にはなりません。）これは基準番号付け(canonical numbering)と呼ばれます。分子構造をグラフ構造とみなせば、グラフ頂点にトポロジーに基づく基準番号を振る作業に対応します。

Morgan法による番号付け

Morgan法はグラフ頂点に整数ラベルを振り、頂点の接続数に基づいてラベルを更新することで、トポロジカルに同じ頂点が同じ整数ラベル持つようにするアルゴリズムです　(HL Morgan: J. Chem. Doc. 5, 107-113, 1965)

アルゴリズムの概略

1. 各頂点 v において、頂点の表す原子番号と隣接する化学結合の数、タイプ（二重結合かどうかなど）から初期ラベル l_v を生成する。
2. ラベルにしたがって頂点を分類する。この時点では結合の数やタイプが同じ原子なら、全て同じラベルを持っている。
3. 各ラベル l_v に、 v に隣接する頂点が持つラベルを全て足しこんで更新する。
   $l_v := l_v + \sum l_w \,( w \in adj(v) )$
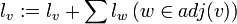
4. ラベルを更新することで頂点の分類が進んでいる限り、ステップ３を繰り返す。
5. ラベルの数にしたがって、番号付けをおこなう。

初期のアルゴリズムは不斉情報を取り扱っていませんでしたが、不斉炭素のパリティをラベルに足しこむという簡単な拡張がSEMA(stereochemically extended Morgan algorithm)法と呼ばれ、現在でも利用されています(WT Wipke, TM Dyott: J Am Chem Soc 96:4834-4842, 1974)。

Morgan（またはSEMA）法は、隣接するラベルを足しこむだけなので、以下の問題点があります。

• 足し算の過程でたまたまラベルが一致してしまうことがある。
• 結合次数が均一のグラフ（例えばinositol)はラベルが同じになってしまうので検出できない。

SMILESによる構造の正規化として提案されている手法は足し算の代わりに掛け算を使っており、問題１が生じる確率を低くしています(D Weininger, A Weininger, JL Weininger: J Chem Inf Comput Sci 29:97-101, 1989)。しかし、問題２の本質的な解決にはなっていません。

正規化の難しさ

一般的なグラフ構造の正規化は難しい問題です。もし正規化が多項式時間で達成できたと仮定しましょう。グラフが正規化されればそのサイズに線形の時間で構造の同一性が確認できるため、グラフの同型問題(Graph Isomorphism Problem)、つまり２つのグラフがトポロジカルに同一かどうかという問題を多項式時間で解いたことになります。しかしこれは現在、クラスPかNPに属することがわかっていない、計算機科学における有名な未解決問題のひとつであり、容易には解けないことが予想されます。（グラフの同型問題は計算機科学以外の分野でしばしばNP-hardと誤解されています。）

グラフがトポロジカルに対称性を持つかどうか、という問いも同じ難しさを持ちます。もしトポロジカルな対称性を多項式時間で解ける場合、グラフ同型を試したい二つのグラフを１本の辺で結んでこのアルゴリズムを適用するだけで同型問題が解けてしまいます（対称なら同型、対称でないなら非同型）。

これまでChemical Informationと呼ばれる分野で数多く提唱されてきたグラフの正規化アルゴリズムはすべて不完全です。特にregular graphと呼ばれる頂点次数が一定のグラフ構造に適用できません。計算機科学の分野では、既に1970年に（隣接頂点だけでなく）離れた頂点までのステップ数による分類を考慮した正規化アルゴリズムが提案されています。

• DG Corneil, CC Gotlib "An efficient algorithm for graph isomorphism" J. Assoc. Comput. Mach. 17 (1) 51-64, 1970.
• DG Corneil, DG Kirkpatrick "A theoretical analysis of various heuristics for the graph isomorphism problem" SIAM J. Comput. 9, 281-297, 1980.

化学分子のようにregularな要素が少ない構造では、このアルゴリズムで十分でしょう (しかしMorgan法だけでは不十分です）。