Aritalab:Lecture/NetworkBiology/Watts-Strogatz Model
m |
|||
| Line 1: | Line 1: | ||
{{Lecture/Header}} | {{Lecture/Header}} | ||
| + | |||
| + | ==スモールワールド== | ||
| + | ディズニーランドに It's a Small World というアトラクションがあります。友達という概念をネットワークで表現すると、世間の狭さは平均頂点間距離 ''L'' が小さいことに相当します。現実のネットワークは平均頂点間距離 ''L'' およびクラスター係数 ''C'' が大きい ( ''L'' = O(log ''N''), ''C'' = 0.2 ∼ 0.3 ) ことが特徴です。 | ||
| + | |||
| + | ランダムグラフ (Erdos-Renyi Model) は ''L'' が小さいものの、''C'' が大きくなりません。 | ||
| + | 逆に格子グラフは ''L'' も ''C'' も大きくなります。これら二つのグラフの特徴を併せ持つモデルを Watts と Strogatz が提唱して一大ブームになりました。 | ||
==歴史と参考図書== | ==歴史と参考図書== | ||
* Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. [http://www.ncbi.nlm.nih.gov/sites/entrez?db=pubmed&uid=9623998&cmd=showdetailview&indexed=google doi:10.1038/30918] | * Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. [http://www.ncbi.nlm.nih.gov/sites/entrez?db=pubmed&uid=9623998&cmd=showdetailview&indexed=google doi:10.1038/30918] | ||
* Durrett R. "Random Graph Dynamics" Cambridge University Press, 2004. | * Durrett R. "Random Graph Dynamics" Cambridge University Press, 2004. | ||
| + | |||
==Watts-Strogatz Model== | ==Watts-Strogatz Model== | ||
| − | 各頂点が<math>k</math>個の隣接点に接続した環状の格子グラフにおいて(総辺数は<math>kn/2</math>)、確率<math>p</math>で辺を張り直したものをWatts- | + | 各頂点が <math>k</math> 個の隣接点に接続した環状の格子グラフにおいて(総辺数は<math>kn/2</math>)、確率 <math>p</math> で辺を張り直したものをWatts-Strogatzモデルといいます。辺を張りなおすモデルだと理論的解析が難しいので、環状の格子グラフにポアソン過程に従って <math>pkn/2</math> 本の辺を追加するモデルがよく使われます。パラメータ <math>p</math> を調節して格子とランダムグラフの中間状態を作成する点がポイントです。 |
| + | |||
| + | === <math>p=0 \,</math> のとき=== | ||
| + | ネットワークは環状の格子グラフです。 | ||
| − | |||
;クラスター係数 | ;クラスター係数 | ||
| − | 簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、<math>k = 2i</math> | + | 簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、 <math>k = 2i</math> とします。注目する点を原点とした <math>-i \leq x, y < \leq i\ </math> のxy座標系を考えたとき、<math>|x - y| > i</math> に対応する座標点は三角形<math>K_3</math>を形成せず、残りは形成します。その割合を考えると <math>C(0) = 3/4</math> です。 |
| + | |||
;平均頂点間距離 | ;平均頂点間距離 | ||
| − | 1ステップで<math>k/2</math>点スキップでき、環状格子で一番離れている点は<math>n/2</math>なので、<math>L(0) \leq n / k</math> | + | 1ステップで <math>k/2</math> 点スキップでき、環状格子で一番離れている点は <math>n/2</math> なので、<math>L(0) \leq n / k</math> となります。 |
| − | ===<math>p=1</math>のとき=== | + | |
| − | + | ===<math>p=1\,</math>のとき=== | |
| + | ネットワークはランダムグラフです。 | ||
| + | |||
;クラスター係数 | ;クラスター係数 | ||
<math>k</math>辺を張りかえるとき、<math>n</math>頂点の中から<math>k</math>隣接点を選べばよいので<math>C(1) \simeq k/n</math>。 | <math>k</math>辺を張りかえるとき、<math>n</math>頂点の中から<math>k</math>隣接点を選べばよいので<math>C(1) \simeq k/n</math>。 | ||
| + | |||
;平均頂点間距離 | ;平均頂点間距離 | ||
辺をランダムに張りかえるので<math>L(1) \simeq \log n / \log k</math>。 | 辺をランダムに張りかえるので<math>L(1) \simeq \log n / \log k</math>。 | ||
Revision as of 21:19, 28 June 2011
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
スモールワールド
ディズニーランドに It's a Small World というアトラクションがあります。友達という概念をネットワークで表現すると、世間の狭さは平均頂点間距離 L が小さいことに相当します。現実のネットワークは平均頂点間距離 L およびクラスター係数 C が大きい ( L = O(log N), C = 0.2 ∼ 0.3 ) ことが特徴です。
ランダムグラフ (Erdos-Renyi Model) は L が小さいものの、C が大きくなりません。 逆に格子グラフは L も C も大きくなります。これら二つのグラフの特徴を併せ持つモデルを Watts と Strogatz が提唱して一大ブームになりました。
歴史と参考図書
- Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. doi:10.1038/30918
- Durrett R. "Random Graph Dynamics" Cambridge University Press, 2004.
Watts-Strogatz Model
各頂点が 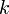 個の隣接点に接続した環状の格子グラフにおいて(総辺数は
個の隣接点に接続した環状の格子グラフにおいて(総辺数は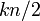 )、確率
)、確率 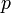 で辺を張り直したものをWatts-Strogatzモデルといいます。辺を張りなおすモデルだと理論的解析が難しいので、環状の格子グラフにポアソン過程に従って
で辺を張り直したものをWatts-Strogatzモデルといいます。辺を張りなおすモデルだと理論的解析が難しいので、環状の格子グラフにポアソン過程に従って 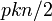 本の辺を追加するモデルがよく使われます。パラメータ
本の辺を追加するモデルがよく使われます。パラメータ 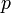 を調節して格子とランダムグラフの中間状態を作成する点がポイントです。
を調節して格子とランダムグラフの中間状態を作成する点がポイントです。
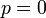 のとき
のとき
ネットワークは環状の格子グラフです。
- クラスター係数
簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、 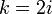 とします。注目する点を原点とした
とします。注目する点を原点とした 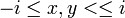 のxy座標系を考えたとき、
のxy座標系を考えたとき、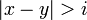 に対応する座標点は三角形
に対応する座標点は三角形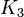 を形成せず、残りは形成します。その割合を考えると
を形成せず、残りは形成します。その割合を考えると 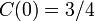 です。
です。
- 平均頂点間距離
1ステップで 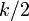 点スキップでき、環状格子で一番離れている点は
点スキップでき、環状格子で一番離れている点は 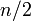 なので、
なので、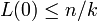 となります。
となります。
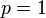 のとき
のとき
ネットワークはランダムグラフです。
- クラスター係数
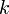 辺を張りかえるとき、
辺を張りかえるとき、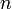 頂点の中から
頂点の中から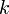 隣接点を選べばよいので
隣接点を選べばよいので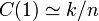 。
。
- 平均頂点間距離
辺をランダムに張りかえるので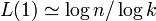 。
。
一般の場合
- 平均頂点間距離
導出は面倒だが以下の近似が知られている。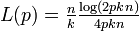
- クラスター係数
簡単な近似では、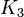 をなす3頂点間の辺が張りなおしを防げばよいので
をなす3頂点間の辺が張りなおしを防げばよいので
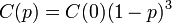 。
。