Aritalab:Lecture/NetworkBiology/Random Walk/Recurrence
m |
m |
||
| Line 1: | Line 1: | ||
| − | == | + | ===二項係数=== |
| + | 左右に移動する確率がそれぞれ p, q のランダムウォークを考えます。原点から出発して 2n ステップ後に再び原点に戻っている確率 <math>p^{(2n)}_{0}</math> は、左右にちょうど n 回ずつ移動すればよいので | ||
| + | |||
| + | <math>\textstyle p^{(2n)}_{0} = \frac{2n!}{n! n!} p^n q^n \ </math> | ||
| + | |||
| + | ここで p(0) = 1 です。スターリングの近似式 <math> n! \sim n^n e^{-n} \sqrt{2\pi n}</math> を使うと | ||
| + | |||
| + | <math>\textstyle | ||
| + | p^{(2n)}_{0} = \frac{2n!}{n! n!} p^{n} q^{n} \sim \frac{(2n)^{2n}e^{-2n} \sqrt{4 \pi n}}{n^{2n} e^{-2n} 2\pi n } p^{n} q^{n} = \frac{(4pq)^n}{\sqrt{\pi n}} | ||
| + | </math> | ||
| + | |||
| + | となります。 | ||
| + | |||
| + | * p = q = 1/2 のとき 4pq = 1 | ||
| + | :<math>\textstyle\sum^{\infty}_{n=0} p^{(2n)}_{0} \sim \sum^{\infty}_{n=0} 1/\sqrt{\pi n} > (1/\sqrt{\pi}) \sum 1/n = \infty </math> なので原点には無限回戻ってくることになり、再帰確実です。 | ||
| + | |||
| + | * p ≠ 1/2 のとき 4pq < 1 | ||
| + | :<math>\textstyle\sum^{\infty}_{n=0} p^{(2n)}_{0} \sim (1/\sqrt{\pi})\sum^{\infty}_{n=0} (4pq)^n/\sqrt{n} \rightarrow N < \infty</math> なので、有限の値に収束し、非再帰的(再帰不確実)です。 | ||
===二項係数と再帰確率=== | ===二項係数と再帰確率=== | ||
Revision as of 23:42, 27 October 2011
Contents |
二項係数
左右に移動する確率がそれぞれ p, q のランダムウォークを考えます。原点から出発して 2n ステップ後に再び原点に戻っている確率 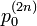 は、左右にちょうど n 回ずつ移動すればよいので
は、左右にちょうど n 回ずつ移動すればよいので
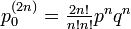
ここで p(0) = 1 です。スターリングの近似式 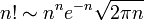 を使うと
を使うと
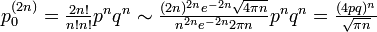
となります。
- p = q = 1/2 のとき 4pq = 1
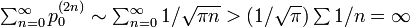 なので原点には無限回戻ってくることになり、再帰確実です。
なので原点には無限回戻ってくることになり、再帰確実です。
- p ≠ 1/2 のとき 4pq < 1
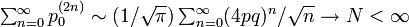 なので、有限の値に収束し、非再帰的(再帰不確実)です。
なので、有限の値に収束し、非再帰的(再帰不確実)です。
二項係数と再帰確率
原点から出発したランダムウォークが原点に戻ってくる確率を再帰確率といいます。
2n に原点に戻る確率を 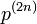 と書き、 2n ステップ後に初めて原点に戻ってくる確率を
と書き、 2n ステップ後に初めて原点に戻ってくる確率を 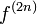 と書きましょう。
と書きましょう。
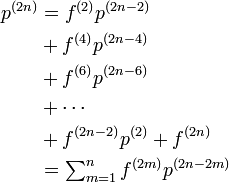
となります。この関係式から
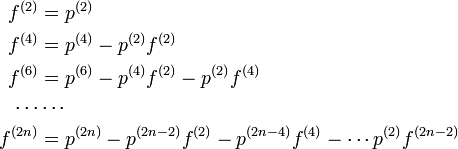
が求まり、二項係数 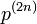 を用いて
を用いて 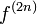 を書き下すことができます。
を書き下すことができます。
再帰確率の母関数
ここでは再帰確率を母関数を用いて求めてみます。 f は 2n 回目で初めて原点に戻ることを意味する関数なので n = 1 からスタートします。この議論の一般形はマルコフ連鎖定常分布のページにも記されています。
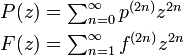
ここで p と f の関係式から
![\begin{align}
p^{(2n)} &= \textstyle\sum^n_{m=1} f^{(2m)} p^{(2n - 2m)}\\
p^{(2n)} z^{2n} & = \textstyle\sum^n_{m=1} f^{(2m)} z^{2m} p^{(2n - 2m)} z^{2n-2m} \\
\textstyle\sum^{\infty}_{n=1} p^{(2n)} z^{2n} & = \textstyle\sum^{\infty}_{n=1}\Big[ \sum^n_{m=1} f^{(2m)} z^{2m} p^{(2n - 2m)} z^{2n-2m} \Big]\\
\end{align}](/mediawiki/images/math/a/b/8/ab819fd98a9a105232b2e3aa8056fc90.png)
さらに
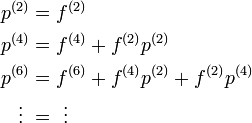
という関係を縦方向に眺めることによって、右辺の2重和の順序を入れ替えます。
![\begin{align}
\textstyle\sum^{\infty}_{n=1} p^{(2n)} z^{2n} &= \textstyle\sum^{\infty}_{n=1}\Big[ \sum^n_{m=1} f^{(2m)} z^{2m} p^{(2n - 2m)} z^{2n-2m} \Big]\\
&= \textstyle\sum^{\infty}_{m=1} f^{(2m)}z^{2m} \sum^{\infty}_{n=m} p^{(2n - 2m)} z^{2n-2m}\\
&= F(z) P(z)
\end{align}](/mediawiki/images/math/0/d/d/0dd742788c9609ff97385c089afb8a41.png)
左辺は 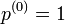 を含まないので
を含まないので 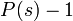 となり、
となり、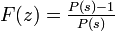 となります。
無限級数
となります。
無限級数 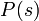 が発散するときは
が発散するときは  となって再帰確実であり(必ず原点にもどる)、有限な値に収束するときは
となって再帰確実であり(必ず原点にもどる)、有限な値に収束するときは 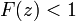 で再帰不確実です。
で再帰不確実です。
実は、二項係数の母関数 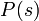 は閉じた式に書き下すことができます。(母関数のページを参照。)
は閉じた式に書き下すことができます。(母関数のページを参照。)
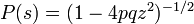
これから
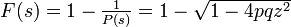
となり再帰確率は
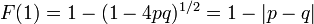
になります。
原点に戻る回数の期待値
再帰確率を r としましょう。ランダムウォークが原点に戻らない確率は (1 − r) です。いったん原点に戻ったら、ランダムウォークを再出発させると考えると、ちょうど1回原点に戻る確率は r (1 − r)、ちょうど2回原点に戻る確率は r2 (1 − r)、ちょうど n 回原点に戻る確率は rn (1 − r) になります。戻る回数の期待値は
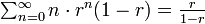
になります(この等式の導出は母関数のページを参照)。一方で、ランダムウォークが原点に戻る回数は n ステップ後に原点にいる確率の総和にも等しいので
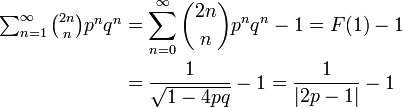
とも書けます(この等式の導出も母関数のページを参照)。
両方の値は等しいので、たとえば p > 1/2 と仮定して
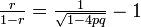
とおけば
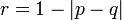
となり、母関数を用いた 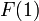 の値と一致します。
の値と一致します。
平均再帰時間
p = q = 1/2 のときだけ再帰確実であり、平均再帰時間を考えられます。
![\textstyle\sum^{\infty}_{n=0} 2n \cdot f^{(2n)} = \Big[ \frac{d F(z)}{dz} \Big]_{z=1} =
[ z(1 - z^2)^{-1/2} ]_{z=1} = \infty](/mediawiki/images/math/4/4/c/44cd1cfedca42f9014a100ab1a049750.png)
つまり、原点には必ず戻りますが無限時間かかる可能性があります。
到達確率
原点から出発して n ステップ後に位置 k に初めて到達する確率 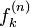 は、再帰確率と同様に求められます。ここでは一般性を失わずに k > 0 とし、 n と k の偶奇が一致する制約を無視して議論を進めます。まず n ステップ後に 位置 k にいる確率
は、再帰確率と同様に求められます。ここでは一般性を失わずに k > 0 とし、 n と k の偶奇が一致する制約を無視して議論を進めます。まず n ステップ後に 位置 k にいる確率 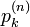 から求めます。
から求めます。
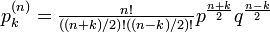
再帰確率の場合と同じく、n ステップ後に初めて k に到達する関数との関係を考えます。初めて k に到達したらそこを原点として残りのステップを関数 p で記述でき、以下になります。
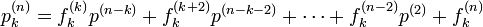
ここで
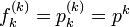
です。二項係数 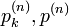 を用いて
を用いて 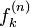 を書き下すことができます。
を書き下すことができます。
k = 1 の場合
原点を出発し、 n ステップ目ではじめて k = 1 になる確率 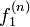 を考えます。
を考えます。
- n = 0 のとき、明らかに
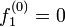
- n = 1 のとき、明らかに
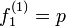
- n > 1 のとき
最初のステップは必ず左です。その後、 m − 1 回 ( m < n ) で右隣の原点に初めて戻り、さらに n − m 回で初めて位置 1 に到達します。その確率は 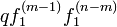 です。m についての和を取ると
です。m についての和を取ると
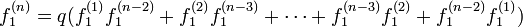
これを n = 2 から並べましょう。
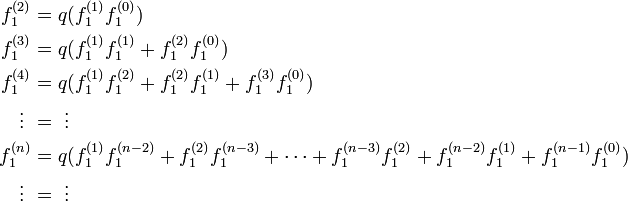
母関数 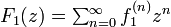 を考慮しながら縦方向に足し合わせます。
を考慮しながら縦方向に足し合わせます。
![\begin{align}
\textstyle\sum^{\infty}_{n=2} f_1^{(n)}z^n &= q \textstyle\sum^{\infty}_{n=2} \sum^{n-1}_{m=1} f_1^{(m)}f_1^{(n-m-1)} z^n\\
F_1(z) - pz &= q z \textstyle\sum^{\infty}_{m=1}f_1^{(m)} z^m \big[ \sum^{\infty}_{n=m+1} f_1^{(n-m-1)} z^{n-m-1}\big]\\
F_1(z) - pz &= q z F_1(z)^2 \\
\end{align}](/mediawiki/images/math/3/5/a/35a2269b0b918d454ebdfa57d48b70d9.png)
この二次式を解くと ![\textstyle F_1(z) = \frac{1}{2qz}[1 - (1 - 4 pqz^2)^{1/2}]](/mediawiki/images/math/d/1/f/d1fc11b449c62a554d01227679d59056.png) となります。(もう一つの解は z = 0 で発散する。)すなわち
となります。(もう一つの解は z = 0 で発散する。)すなわち

もし p < q (左のほうに行く確率が高い)なら、永遠に待っていても 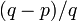 の確率で k = 1 に来ることはなく、p ≥ q の場合は必ず k = 1 に到達します。
の確率で k = 1 に来ることはなく、p ≥ q の場合は必ず k = 1 に到達します。