Aritalab:Lecture/NetworkBiology/Random Walk
m |
m |
||
| Line 1: | Line 1: | ||
{{Lecture/Header}} | {{Lecture/Header}} | ||
| − | == | + | ==1次元のランダムウォーク== |
| − | + | 原点から出発して1ステップ毎に確率 ''p'' で + 1, ''q'' (= 1 − ''p'') で − 1 動くランダムウォークを考えましょう。 | |
| − | 原点から出発して1ステップ毎に確率 ''p'' で +1, 1 | + | |
''n'' ステップ後に、正の方向に ''k'' 回進んでいる確率は | ''n'' ステップ後に、正の方向に ''k'' 回進んでいる確率は | ||
| − | <center> <sub>n</sub><big>C</big><sub>k</sub> ''p<sup>k</sup>'' | + | <center> <sub>n</sub><big>C</big><sub>k</sub> ''p<sup>k</sup>'' ''q<sup>n - k</sup>'' </center> |
| − | であらわされ、二項分布 (英語でbinomial distributionといいます) B(''n'', ''p'' ) に従います。位置の期待値は ''np'' <ref>期待値の定義に従って計算します。 | + | であらわされ、二項分布 (英語でbinomial distributionといいます) B( ''n'', ''p'' ) に従います。位置の期待値は ''np'' <ref>期待値の定義に従って計算します。 |
<math> | <math> | ||
| Line 15: | Line 14: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | </ref>, 分散は '' | + | </ref>, 分散は ''npq'' <ref>分散の定義に従って計算します。まず |
<math> | <math> | ||
| Line 32: | Line 31: | ||
</math> | </math> | ||
</ref>です。 | </ref>です。 | ||
| + | |||
| + | ===再帰性=== | ||
| + | 原点から出発したランダムウォークが原点に戻ってくる確率を再帰確率といい、''p'' = ''q'' = 1/2 の時に限って 1 になります。確率 1 で原点に戻るとき、ウォークは再帰的であるといいます。''p'' ≠ 1/2 のときウォークは再帰的でなく、再帰確率は 1 − |''p'' − ''q''| になります<ref> | ||
| + | 再帰確率を ''r'' としましょう。ランダムウォークが原点に戻ってこない確率は (1 − ''r'') です。いったん原点に戻ってきたら、ランダムウォークを再出発させると考えると、ちょうど1回原点に戻ってくる確率は ''r'' (1 − ''r'' )、ちょうど2回原点に戻ってくる確率は ''r''<sup>2</sup> (1 − ''r'' )、ちょうど ''n'' 回原点に戻ってくる確率は ''r''<sup>''n''</sup> (1 − ''r'' ) になります。戻ってくる回数の期待値は | ||
| + | |||
| + | <math>\textstyle \sum^{\infty}_{n=0} n \cdot r^n (1-r) = \frac{r}{1-r}</math> | ||
| + | |||
| + | になります(この等式の導出は[[Aritalab:Lecture/Basic/Generating_Function|母関数]]のページを参照)。一方で、ランダムウォークが原点に戻ってくる回数は ''n'' ステップ後に原点にいる確率をすべて足し合わせたものに等しいので | ||
| + | |||
| + | <math>\textstyle \sum^{\infty}_{n=1} \binom{2n}{n} p^nq^n = \sum^{\infty}_{n=0} \binom{2n}{n} p^nq^n - 1 = \frac{1}{\sqrt{1 - 4pq}} - 1 = \frac{1}{|2p - 1|} - 1</math> | ||
| + | |||
| + | とも書けます(この等式の導出も[[Aritalab:Lecture/Basic/Generating_Function|母関数]]のページを参照)。戻ってくる回数の期待値は ''p'' = 1 のときは 0 となり、 ''p'' が 1/2 に近づくにつれて無限回に増えるわけです。この値が ''r'' / (1 − ''r'') に等しいので、たとえば ''p'' > 1/2 と仮定して ''r'' / (1 − ''r'') = −1 + 1 / (2 ''p'' − 1) とおけば ''r'' = 2 ''q'' = 1 − |''p'' − ''q''| となります。 | ||
| + | </ref>。 | ||
| + | |||
| + | 再帰的な場合、つまり ''p'' = ''q'' = 1/2 であれば、戻るまでの期待時間を考えることは意味があります。 | ||
| + | これを平均再帰時間といい ''n'' ステップ後にはじめて原点に戻ってくる確率に ''n'' をかけて和をとると求まります。一次元のランダムウォークでも平均再帰時間は無限大になります。 | ||
| + | |||
| + | ;例 | ||
| + | : 公正なコインによる賭けでは、どんなに負けていても賭けを継続していれば収支は必ず 0 に戻せる(再帰性)。 | ||
| + | |||
| + | |||
| + | |||
| + | ===ギャンブラーの破産問題=== | ||
| + | 二人のプレーヤーがコインを ''k''<sub>1</sub> と ''k''<sub>2</sub> 枚ずつ持っています。確率 1/2 で勝てばコインを 1 枚うけとり、負ければ 1 枚渡します。勝負は原点から出発して 1/2 に移動するランダムウォークに相当し、時刻 ''t'' における位置はプレーヤー 1 が勝った数とします。状態 − ''k''<sub>1</sub> になったらプレーヤー 1 が破産してゲームは終了し、''k''<sub>2</sub> になったらプレーヤー 2 が破産してゲームは終了します。このゲームは、状態 ''k''<sub>1</sub> と ''k''<sub>2</sub> が吸収状態になっているマルコフ連鎖とみなせます。プレーヤー 1 が破産する前に ''k''<sub>2</sub> 枚のコインを獲得する確率 ''q'' を求めましょう。 | ||
| + | |||
| + | 時刻 ''t'' において位置が ''i'' である確率を<math>P^t_{i}</math> と書きましょう。すると | ||
| + | |||
| + | <math>\textstyle \lim_{t\rightarrow \infty} P^t_{-k_1} = 1-q,\ \lim_{t\rightarrow \infty} P^t_{k_2} = q,\ \lim_{t\rightarrow \infty} P^t_{i} = 0 (-k_1 < i < k_2) </math> | ||
| + | |||
| + | となります。また、ゲームは公正なため、どの位置にいようとプレーヤー 1 がコインを得る期待値は 0 になります。つまり | ||
| + | |||
| + | <math>\textstyle \sum^{k_2}_{i = -k_1} i P^t_{i} = 0</math> | ||
| + | |||
| + | です。極限を取ると | ||
| + | |||
| + | <math>\textstyle \lim_{t\rightarrow \infty} \sum^{k_2}_{i = -k_1} i P^t_{i} = k_2 q - k_1 (1-q) = 0 </math> | ||
| + | |||
| + | となるので <math> q = k_1 / (k_1 + k_2) </math> です。つまりゲームに勝つ確率は、開始時の持ち点に比例します。 | ||
| + | |||
| + | ;例 | ||
| + | : 公正なコインを用いた賭けでも、資金が少ないギャンブラーが資金の多い胴元に勝つ見込みは少ない。 | ||
== グラフ上のランダムウォーク == | == グラフ上のランダムウォーク == | ||
| − | グラフ | + | グラフ G( ''V'' , ''E'' ) の各頂点 ''u'' から出る辺を等確率 <math>1/d(u)</math> で選んで動くグラフ上のランダムウォークを考えましょう。非周期性を仮定したいので、以下では二部グラフでない連結なものだけを考慮します。 |
| − | + | ||
| − | '''[定理]''' 頂点 ''u'' から ''v'' に到達するステップ数の期待値を <math>h_{u,v}</math> と記述すると <math>\textstyle h_{u,u} = \frac{2|E|}{d(u)}</math> | + | '''[定理]''' 頂点 ''u'' から ''v'' に到達するステップ数の期待値を <math>h_{u,v}</math> と記述すると <math>\textstyle h_{u,u} = \frac{2|E|}{d(u)}</math> が成立する。 |
;証明 | ;証明 | ||
| − | まずランダムウォークの定常分布 <math>\bar \pi</math> が <math>\textstyle \frac{d(v)}{2|E|}</math> | + | まずランダムウォークの定常分布 <math>\bar \pi</math> が 各頂点 ''v'' において<math>\pi_v = \textstyle \frac{d(v)}{2|E|}</math> であると仮定してみましょう。 |
| − | + | 各頂点上の確率 <math>\pi_v</math> の総和をとると <math>\textstyle \sum_{v \in V} \pi_v = \sum_{v \in V} \frac{d(v)}{2 |E|} = 1</math>。 | |
また | また | ||
| Line 49: | Line 88: | ||
= \sum_{u \in adj(v)} \frac{1}{2 |E|} = \frac{d(v)}{2|E|} = \bar \pi | = \sum_{u \in adj(v)} \frac{1}{2 |E|} = \frac{d(v)}{2|E|} = \bar \pi | ||
</math> から、 | </math> から、 | ||
| − | <math>\textstyle \frac{d(v)}{2|E|}</math> | + | <math>\textstyle \frac{d(v)}{2|E|}</math> は定常分布の条件を満たしています。 |
| − | + | 各頂点への再帰時間の期待値は <math>\textstyle 1/\pi_u </math> になるので、証明は終わりです。 | |
| − | + | '''[補題]''' 隣り合う頂点間のステップ数の期待値の上限は <math> 2 |E|</math> で抑えられる。 | |
| − | + | ;証明 | |
| + | 各頂点への再帰時間の期待値を、二通りに計算してみます。 | ||
| + | <math>\textstyle h_{u,u} = 2 |E| / d(u) | ||
| + | = \frac{1}{d(u)} \sum_{v \in adj(u)} (1+ h_{v,u})</math> | ||
| − | <math>\textstyle | + | つまり <math>\textstyle 2 |E| = \sum_{v \in adj(u)} (1+ h_{v,u})</math> ですから <math> 2 |E| > h_{v,u} </math> です。 |
| − | 2|E| | + | |
| − | = \sum_{v \in adj(u)} (1+ h_{v,u}) > h_{v,u}</math> | + | |
| − | + | '''[補題]''' グラフ全体を訪れるのに必要な期待値の上限は <math>4 |V| |E|</math> で抑えられる。 | |
| + | |||
| + | ;証明 | ||
| + | 与えられたグラフ全体をスパンする木を作ります。その上を全点辿ったときの辺数は <math>(2|V|-2)</math> です。 | ||
<math>\textstyle | <math>\textstyle | ||
| Line 67: | Line 110: | ||
</math> | </math> | ||
| − | このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) | + | このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) と呼びます。 |
| − | + | ||
| + | ==参考:式の導出== | ||
| + | 本文中に出てくる式の導出です。 | ||
<references/> | <references/> | ||
Revision as of 02:34, 26 May 2011
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
1次元のランダムウォーク
原点から出発して1ステップ毎に確率 p で + 1, q (= 1 − p) で − 1 動くランダムウォークを考えましょう。 n ステップ後に、正の方向に k 回進んでいる確率は
であらわされ、二項分布 (英語でbinomial distributionといいます) B( n, p ) に従います。位置の期待値は np [1], 分散は npq [2]です。
再帰性
原点から出発したランダムウォークが原点に戻ってくる確率を再帰確率といい、p = q = 1/2 の時に限って 1 になります。確率 1 で原点に戻るとき、ウォークは再帰的であるといいます。p ≠ 1/2 のときウォークは再帰的でなく、再帰確率は 1 − |p − q| になります[3]。
再帰的な場合、つまり p = q = 1/2 であれば、戻るまでの期待時間を考えることは意味があります。 これを平均再帰時間といい n ステップ後にはじめて原点に戻ってくる確率に n をかけて和をとると求まります。一次元のランダムウォークでも平均再帰時間は無限大になります。
- 例
- 公正なコインによる賭けでは、どんなに負けていても賭けを継続していれば収支は必ず 0 に戻せる(再帰性)。
ギャンブラーの破産問題
二人のプレーヤーがコインを k1 と k2 枚ずつ持っています。確率 1/2 で勝てばコインを 1 枚うけとり、負ければ 1 枚渡します。勝負は原点から出発して 1/2 に移動するランダムウォークに相当し、時刻 t における位置はプレーヤー 1 が勝った数とします。状態 − k1 になったらプレーヤー 1 が破産してゲームは終了し、k2 になったらプレーヤー 2 が破産してゲームは終了します。このゲームは、状態 k1 と k2 が吸収状態になっているマルコフ連鎖とみなせます。プレーヤー 1 が破産する前に k2 枚のコインを獲得する確率 q を求めましょう。
時刻 t において位置が i である確率を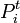 と書きましょう。すると
と書きましょう。すると
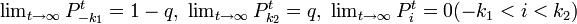
となります。また、ゲームは公正なため、どの位置にいようとプレーヤー 1 がコインを得る期待値は 0 になります。つまり
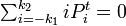
です。極限を取ると
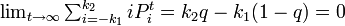
となるので 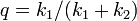 です。つまりゲームに勝つ確率は、開始時の持ち点に比例します。
です。つまりゲームに勝つ確率は、開始時の持ち点に比例します。
- 例
- 公正なコインを用いた賭けでも、資金が少ないギャンブラーが資金の多い胴元に勝つ見込みは少ない。
グラフ上のランダムウォーク
グラフ G( V , E ) の各頂点 u から出る辺を等確率 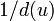 で選んで動くグラフ上のランダムウォークを考えましょう。非周期性を仮定したいので、以下では二部グラフでない連結なものだけを考慮します。
で選んで動くグラフ上のランダムウォークを考えましょう。非周期性を仮定したいので、以下では二部グラフでない連結なものだけを考慮します。
[定理] 頂点 u から v に到達するステップ数の期待値を 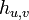 と記述すると
と記述すると 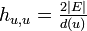 が成立する。
が成立する。
- 証明
まずランダムウォークの定常分布 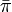 が 各頂点 v において
が 各頂点 v において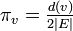 であると仮定してみましょう。
各頂点上の確率
であると仮定してみましょう。
各頂点上の確率 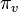 の総和をとると
の総和をとると 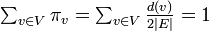 。
。
また
Failed to parse (lexing error): \textstyle \bar \pi {\mathbf P} = \sum_{u \in adj(v)} \pi_u \frac{1}{d(u)} = \sum_{u \in adj(v)} \frac{1}{2 |E|} = \frac{d(v)}{2|E|} = \bar \pi
から、
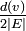 は定常分布の条件を満たしています。
は定常分布の条件を満たしています。
各頂点への再帰時間の期待値は 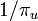 になるので、証明は終わりです。
になるので、証明は終わりです。
[補題] 隣り合う頂点間のステップ数の期待値の上限は 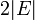 で抑えられる。
で抑えられる。
- 証明
各頂点への再帰時間の期待値を、二通りに計算してみます。
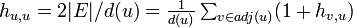
つまり 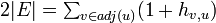 ですから
ですから 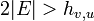 です。
です。
[補題] グラフ全体を訪れるのに必要な期待値の上限は 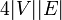 で抑えられる。
で抑えられる。
- 証明
与えられたグラフ全体をスパンする木を作ります。その上を全点辿ったときの辺数は 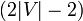 です。
です。
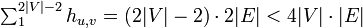
このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) と呼びます。
参考:式の導出
本文中に出てくる式の導出です。
- ↑ 期待値の定義に従って計算します。
![\begin{align}
E[X] &= \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=1}^n k \binom{n}{k} p^k(1-p)^{n-k}\\
&= \sum_{k=1}^n k \frac{n}{k} \binom{n-1}{k-1} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n}{k} \cdot p \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k}\\
&= np \sum^{n}_{k=1} \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k} = np
\end{align}](/mediawiki/images/math/3/e/6/3e62873053db052b373dd8858582045f.png)
- ↑ 分散の定義に従って計算します。まず
![\begin{align}
E[X^2] &= k^2 \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=0}^n {k(k-1)+k} \binom{n}{k} p^k(1-p)^{n-k}\\
&= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k}\\
&= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + np \\
&= n(n-1) \sum_{k=2}^n k(k-1) \binom{n-2}{k-2} p^{k-2}(1-p)^{n-k} + np \\
&= n(n-1) p^2 + np
\end{align}](/mediawiki/images/math/c/e/a/cea507a5fa466b803f158dbe0908b7f0.png)
したがって
![\begin{align}
V[X] &= E[X^2] - (E[X])^2 = n(n-1) p^2 + np - n^2p^2\\
&= np (1-p)
\end{align}](/mediawiki/images/math/4/3/9/439bd925821dc9370834e8ffa8e38e42.png)
- ↑
再帰確率を r としましょう。ランダムウォークが原点に戻ってこない確率は (1 − r) です。いったん原点に戻ってきたら、ランダムウォークを再出発させると考えると、ちょうど1回原点に戻ってくる確率は r (1 − r )、ちょうど2回原点に戻ってくる確率は r2 (1 − r )、ちょうど n 回原点に戻ってくる確率は rn (1 − r ) になります。戻ってくる回数の期待値は
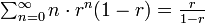 になります(この等式の導出は母関数のページを参照)。一方で、ランダムウォークが原点に戻ってくる回数は n ステップ後に原点にいる確率をすべて足し合わせたものに等しいので
になります(この等式の導出は母関数のページを参照)。一方で、ランダムウォークが原点に戻ってくる回数は n ステップ後に原点にいる確率をすべて足し合わせたものに等しいので
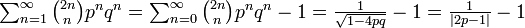 とも書けます(この等式の導出も母関数のページを参照)。戻ってくる回数の期待値は p = 1 のときは 0 となり、 p が 1/2 に近づくにつれて無限回に増えるわけです。この値が r / (1 − r) に等しいので、たとえば p > 1/2 と仮定して r / (1 − r) = −1 + 1 / (2 p − 1) とおけば r = 2 q = 1 − |p − q| となります。
とも書けます(この等式の導出も母関数のページを参照)。戻ってくる回数の期待値は p = 1 のときは 0 となり、 p が 1/2 に近づくにつれて無限回に増えるわけです。この値が r / (1 − r) に等しいので、たとえば p > 1/2 と仮定して r / (1 − r) = −1 + 1 / (2 p − 1) とおけば r = 2 q = 1 − |p − q| となります。