Aritalab:Lecture/NetworkBiology/Percolation on Graph
m (→占有される頂点の母関数) |
m (→占有される頂点の母関数) |
||
| Line 44: | Line 44: | ||
\begin{align} | \begin{align} | ||
F'_v(1) &= q G'_v(1) = q \langle k \rangle \\ | F'_v(1) &= q G'_v(1) = q \langle k \rangle \\ | ||
| − | F''_v(1) &= q^2G''_v(1) = q^2 \langle k^2 \rangle - q \langle k \rangle | + | F''_v(1) &= q^2G''_v(1) - q G'_v(1) = q^2 \langle k^2 \rangle - q \langle k \rangle |
\end{align} | \end{align} | ||
</math> | </math> | ||
Revision as of 09:33, 17 January 2014
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
グラフ上のパーコレーション
グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみます。 この内容を読む前に母関数の概念を復習しておいてください。
次数分布の母関数
グラフの次数分布 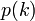 を与えられたとき、その母関数は
を与えられたとき、その母関数は
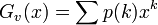
になります。しかし、頂点 v の隣にある頂点 w の次数分布はもはや 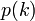 ではありません。
選ばれた辺の先には、他の点が等確率でくることはないからです。
辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えましょう。
次数の大きい点のほうが、次数に比例して存在する確率が高くなります。
つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した
ではありません。
選ばれた辺の先には、他の点が等確率でくることはないからです。
辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えましょう。
次数の大きい点のほうが、次数に比例して存在する確率が高くなります。
つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した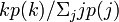 となります(分母は正規化定数)。
よってある頂点 v の隣にくる頂点 w の次数分布の母関数は
となります(分母は正規化定数)。
よってある頂点 v の隣にくる頂点 w の次数分布の母関数は
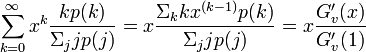
母関数においては、次数 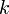 に対して
に対して 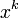 が対応します。
頂点 v の先に w がついているとき、w から v 以外に伸びる辺数に注目しましょう。
v から w への辺1本ぶんを除いた w に関する母関数は、上の式を
が対応します。
頂点 v の先に w がついているとき、w から v 以外に伸びる辺数に注目しましょう。
v から w への辺1本ぶんを除いた w に関する母関数は、上の式を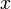 で割ったものにあたります。
で割ったものにあたります。
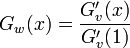
占有される頂点の母関数
パーコレーションで相転移が起きるのは、頂点から伸びていく辺の期待値が1をちょうど超えるときです。
ただし、このときの母関数はグラフ全体の次数分布を示す 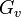 ではなく、占有された頂点のみによる部分ネットワークの母関数です。
したがって、母関数を区別して
ではなく、占有された頂点のみによる部分ネットワークの母関数です。
したがって、母関数を区別して 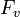 と記しましょう。関数 F と G の関係は、各頂点が確率 q で占有されるため G と F の次数平均をそれぞれ
と記しましょう。関数 F と G の関係は、各頂点が確率 q で占有されるため G と F の次数平均をそれぞれ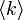 ,
, 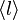 と書くと
と書くと
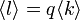 です。
です。
この関係から (式の導出は確率母関数のページを参照)
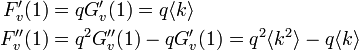
相転移が起きるのは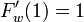 のときです。
のときです。
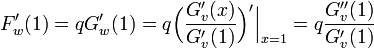
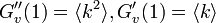 を代入すると
を代入すると
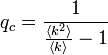
すなわち、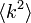 が大きく
が大きく 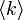 を上回るときに
を上回るときに 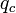 は小さくなります。
ハブの k は大きくなりますから、
は小さくなります。
ハブの k は大きくなりますから、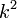 は更に大きくなります。次数の大きなハブがあるほど、パーコレーションが起きやすいということです。また全ての次数が同じとき、
は更に大きくなります。次数の大きなハブがあるほど、パーコレーションが起きやすいということです。また全ての次数が同じとき、 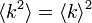 となりベーテ格子の結果と一致します。
となりベーテ格子の結果と一致します。
パーコレーションの起こりやすさ
いかなる次数分布でも、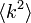 が
が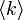 に比して大きいと、低い浸透確率で相転移が起こることをみてきました。
に比して大きいと、低い浸透確率で相転移が起こることをみてきました。
ランダムグラフの場合
次数の分布がポアソン分布になるランダムグラフをかんがえましょう。平均と分散は等しく ![E[k] = V[k] = \langle k \rangle](/mediawiki/images/math/a/0/8/a08c7b8e48d6939e5f49fc09c58327bc.png) になります。
このとき
になります。
このとき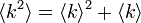 になるので
になるので
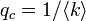
すなわち、平均次数に反比例して浸透確率が下がっていきます。
スケールフリーネットワークの場合
次数の分布が、べき分布 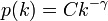 のときをかんがえましょう。
ここで
のときをかんがえましょう。
ここで 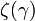 はリーマンゼータ関数とします。
はリーマンゼータ関数とします。
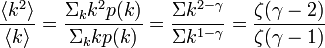
この値は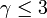 のときに発散します。また
のときに発散します。また 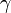 が大きくなると
が大きくなると 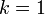 の項が大きな要素を占めるのでほとんど 1 に近づきます。
の項が大きな要素を占めるのでほとんど 1 に近づきます。