Aritalab:Lecture/NetworkBiology/Percolation on Graph
m (→パーコレーション) |
|||
| Line 62: | Line 62: | ||
==パーコレーション== | ==パーコレーション== | ||
| − | いかなる次数分布でも、<math>\langle k^2 \rangle</math>が<math>\langle k \rangle</math> | + | いかなる次数分布でも、<math>\langle k^2 \rangle</math>が<math>\langle k \rangle</math>に比して大きいと、低い浸透確率で相転移が起こることを見た。 |
===ランダムグラフの場合=== | ===ランダムグラフの場合=== | ||
| Line 70: | Line 70: | ||
<math>q_c = 1 / \langle k \rangle</math> | <math>q_c = 1 / \langle k \rangle</math> | ||
| − | + | すなわち、平均次数が大きくなるほど浸透しやすくなる。 | |
===スケールフリーネットワークの場合=== | ===スケールフリーネットワークの場合=== | ||
| Line 80: | Line 80: | ||
</math> | </math> | ||
| − | この値は<math>\gamma \leq 3</math> | + | この値は<math>\gamma \leq 3</math>のときに発散する。有限のネットワークではその値も有限だが、大きな値になるために非常に低い値で浸透すると考えてよい。 |
| − | + | ||
<!---- | <!---- | ||
| Line 96: | Line 95: | ||
パーコレーションにおいては、確率<math>(1-q)</math>で辺が繋がらなくなる。実効的な次数が<math>\bar{k}</math>になる確率は<math>\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}</math>である。 | パーコレーションにおいては、確率<math>(1-q)</math>で辺が繋がらなくなる。実効的な次数が<math>\bar{k}</math>になる確率は<math>\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}</math>である。 | ||
| − | + | ||
このとき<math>\langle \bar{k} \rangle = \langle k \rangle q</math>、<math>\langle \bar{k^2} \rangle = \langle k^2 \rangle + \langle k \rangle q (1-q)</math>になる。 | このとき<math>\langle \bar{k} \rangle = \langle k \rangle q</math>、<math>\langle \bar{k^2} \rangle = \langle k^2 \rangle + \langle k \rangle q (1-q)</math>になる。 | ||
大雑把に言うと相転移を起こすのは<math>\langle k^2 \rangle q^2= 2 \langle k \rangle q</math>のとき、つまり<math>q = 2 \langle k \rangle / \langle k^2 \rangle</math>のあたりである。 | 大雑把に言うと相転移を起こすのは<math>\langle k^2 \rangle q^2= 2 \langle k \rangle q</math>のとき、つまり<math>q = 2 \langle k \rangle / \langle k^2 \rangle</math>のあたりである。 | ||
| − | + | ----> | |
| − | + | ||
| − | ---> | + | |
Revision as of 23:25, 13 June 2010
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
グラフ上のパーコレーション
グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみよう。 ここでは母関数という概念を利用する。
次数分布の母関数
グラフの次数分布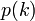 を与えられたとき、その母関数は
を与えられたとき、その母関数は
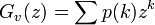
しかし、頂点vの隣にある頂点wの次数分布はもはや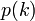 ではない。
辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えよう。
選ばれた辺の先には、他の点が等確率でくることはない。次数の大きい点のほうが、次数に比例して存在する確率が高くなるだろう。
つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した
ではない。
辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えよう。
選ばれた辺の先には、他の点が等確率でくることはない。次数の大きい点のほうが、次数に比例して存在する確率が高くなるだろう。
つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した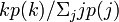 となる(分母は正規化定数)。
よってある頂点vの隣にある頂点wの次数分布の母関数は
となる(分母は正規化定数)。
よってある頂点vの隣にある頂点wの次数分布の母関数は
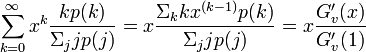
母関数においては、次数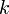 に対して
に対して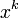 が対応する。
頂点vの先にwがついているとき、wからv以外に伸びる辺数に注目しよう。
vからwへの辺1本を除いた、wに関する母関数は上の式を
が対応する。
頂点vの先にwがついているとき、wからv以外に伸びる辺数に注目しよう。
vからwへの辺1本を除いた、wに関する母関数は上の式を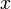 で割ればよい。
で割ればよい。
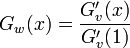
占有される頂点の母関数
パーコレーションで相転移が起きるのは、頂点から伸びていく辺の期待値が1をちょうど超えるときである。
ただし、このときの母関数はグラフ全体の次数分布を示す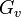 ではなく、占有された頂点のみによる部分ネットワークの母関数である。
したがって、母関数を区別して
ではなく、占有された頂点のみによる部分ネットワークの母関数である。
したがって、母関数を区別して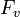 と記そう。FとGの関係は、各頂点が確率qで占有されるためGとFの次数平均をそれぞれ
と記そう。FとGの関係は、各頂点が確率qで占有されるためGとFの次数平均をそれぞれ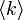 ,
, 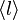 と書くと
と書くと
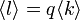
この関係から
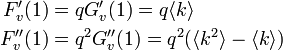
相転移が起きるのは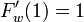 のときだから
のときだから
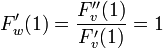
代入すると
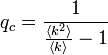
すなわち、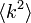 が大きく
が大きく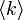 を上回るとき、
を上回るとき、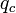 は小さくなる。
は小さくなる。
パーコレーション
いかなる次数分布でも、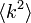 が
が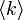 に比して大きいと、低い浸透確率で相転移が起こることを見た。
に比して大きいと、低い浸透確率で相転移が起こることを見た。
ランダムグラフの場合
ランダムグラフの場合は次数分布がポアソン分布になる。このとき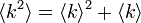 になるので
になるので
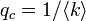
すなわち、平均次数が大きくなるほど浸透しやすくなる。
スケールフリーネットワークの場合
べき分布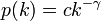 のとき
のとき
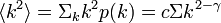
この値はFailed to parse (lexing error): \gamma \leq 3 のときに発散する。有限のネットワークではその値も有限だが、大きな値になるために非常に低い値で浸透すると考えてよい。