Aritalab:Lecture/NetworkBiology/Diffusion
Contents |
ランダムウォークとブラウン運動
数直線上で原点から出発するランダムウォークが左(負の方向)にいく確率を q 右(正の方向)にいく確率を p とします。ここで p + q = 1 です。時刻 t において位置 x にいる確率を u ( x , t ) と書いて漸化式を作ると
となります。ここで Δx が歩幅、Δt が単位時間です。この式で右側をテイラー展開してみます。
u( x , t ) を移項して全体を Δ t で割ります。
ここで以下の収束条件を仮定します。
式を書きなおすと 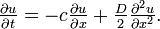
このとき、離散時間のランダムウォークから話を始めましたが u ( x , t ) は連続時間・連続位置の確率分布関数になっています。これをドリフトつき拡散方程式と呼びます。また、前向きのコルモゴロフ微分方程式とも呼ばれます。
p = q = 1/2 のとき、c = 0 となります。この場合をブラウン運動と呼びます。さらに D = 1 のとき、標準ブラウン運動、またはウィーナー過程と呼びます。 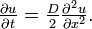
この方程式を解くには初期条件が必要です。時刻 0 において確率 1 で位置 0 にいると仮定すると、解は平均が ct 分散が Dt の正規分布になります。
ここで上記の収束条件は重要です。分散と平均が有限値に収まるためには c, D が有限値に収束しなくてはなりません。
拡散過程
連続時間の確率過程 { X(t) : t ∈ [ 0, ∞ ) } における次状態が、現在の状態にのみ依存する場合をマルコフ過程と呼びます。
時刻 t で状態 x から、時刻 s で状態 y に遷移したとき、その確率密度関数を p ( y, s; x, t ) とかきます。ここでは時間について一様 (homogenious) であることを仮定します。
- p ( y, s + Δt; x, t + Δt) = p ( y, s; x, t )
つまり Δ 時間ずらしても遷移に影響はありません。連続時間のマルコフ過程が如何なる ε >0 に対しても次の条件を満たすとき、それを拡散過程と呼びます。
1. 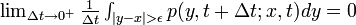
- (微小時間 Δ t における、ε近傍より大きな移動は無視できる)
2. 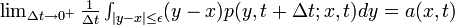
- (微小時間 Δ t における移動距離の平均値は a)
3. 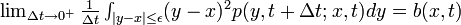
- (微小時間 Δ t における移動距離の分散は b)
これらの式はより条件の厳しい以下の式から導けます。
1'. 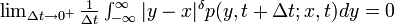 for some δ > 2
for some δ > 2
2'. 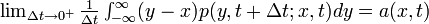
3'. 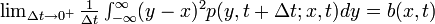
この式は平均や分散を使って y - x = ΔX(t) と書きなおせば
1'. ![\textstyle\lim_{\Delta t \rightarrow 0^+} \frac{1}{\Delta t} E( [\Delta X(t)]^{\delta} | X(t) = x) = 0](/mediawiki/images/math/b/1/1/b111873f185613a79a6ee444900ceb41.png) for some δ > 2
for some δ > 2
2'. 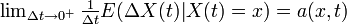
3'. ![\textstyle\lim_{\Delta t \rightarrow 0^+} \frac{1}{\Delta t} E( [\Delta X(t)]^2 | X(t) = x) = b(x,t)](/mediawiki/images/math/f/0/9/f0975974c56ed02acf4fa81a3086f4ed.png)
となります。条件 1'は ε近傍も含めて 3 次以上の項が 0 になることを示しています。また ε 近傍より大きなところでは
が成立するので、2'および3'が成立する際には収束する成分は ε 近傍内に限られます。
Kolmogorov 微分方程式
コルモゴロフ微分方程式には前向きと後ろ向きがあります。遷移確率が移動先(未来)の状態、あるいは移動元(過去)の状態を用いて記述されるかの違いです。平均と分散の収束先である係数 a(y,t), b(y,t) を時間に非依存としてそれぞれ a(y), b(y) として書いています。
- 前向き方程式: (y,s) を用いて記述
-
![\textstyle \frac{\partial p(y,s;x,t)}{\partial s} = - \frac{\partial [a(y)p(y,s;x,t)]}{\partial y} + \frac{1}{2} \frac{\partial^2[b(y)p(y,s;x,t)]}{\partial y^2}](/mediawiki/images/math/4/e/0/4e0ed30975b7a0bbd1848359588b2812.png) (Fokker-Planck 等式とも呼ばれる)
(Fokker-Planck 等式とも呼ばれる)
- 後ろ向き方程式: (x,t) を用いて記述
以下のChapman-Kolmogorov等式と
という式を使って z についてテーラー展開します。
ここで両辺を Δ t で割って Δ t → 0 とおけば後ろ向きの微分方程式が得られます。
コルモゴロフ微分方程式が解を持つかどうかは、係数 a(x), b(x) や空間に依存します。ある位置で b(x) = 0 が成り立つ場合、式は singular と呼ばれ、空間全体 (-∞, ∞) で解を持つことはありません。解を持つには b(x) > 0 であることが必要です。
ある領域 (r1 , r2) で如何なる点へもその他の点から移動可能な場合、regular といい(既約なマルコフ連鎖に相当)、その場合を考えましょう。境界 ri は到達可能な場合と到達不可能な場合があり、
- 到達可能 (accessible)
- regular ... 反射壁のように移動を続けられる
- exit ... 吸収状態に同じ
- 到達不可能 (inaccessible)
- natural ... 確率的に移動できない (例えば無限遠点)
- entrance ... スタート地点だがここには戻れない
に分けられます。
例 8.2
- a (x) = α x , b (x) = β x の場合
前向きコルモゴロフ微分方程式は
となり、指数的な増加(減少)プロセスになります。平均値 μX(t) の時間変化を計算すると 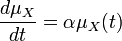 となるので、これを解くと
となるので、これを解くと 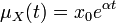 、つまり平均値は指数的に増加します。これは、出生過程と似たプロセスです。
、つまり平均値は指数的に増加します。これは、出生過程と似たプロセスです。
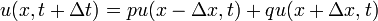
![\begin{align}
u(x, t+ \Delta t) &= \textstyle p \Big[ u(x,t) + \frac{\partial u(x,t)}{\partial x} (- \Delta x) + \frac{\partial^2 u(x,t)}{\partial x^2} \frac{(\Delta x)^2}{2} + O((\Delta x)^3) \Big] \\
& \textstyle + q \Big[ u(x,t) + \frac{\partial u(x,t)}{\partial x} (\Delta x) + \frac{\partial^2 u(x,t)}{\partial x^2} \frac{(\Delta x)^2}{2} + O((\Delta x)^3) \Big] \\
&= \textstyle u(x,t) + (q-p)\frac{\partial u(x,t)}{\partial x} \Delta x + \frac{\partial^2 u(x,t)}{\partial x^2} \frac{(\Delta x)^2}{2} + O((\Delta x)^3) \Big].
\end{align}](/mediawiki/images/math/4/8/f/48f82057603bb9187052a722891b1e9c.png)
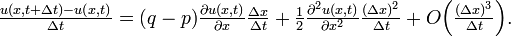
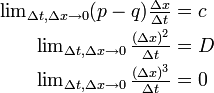
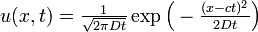
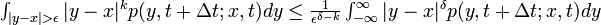
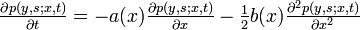
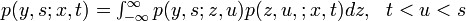
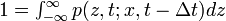
![\begin{align}
\textstyle & p(y,s;x,t-\Delta t) - p(y,s;x,t)\\
&=\textstyle [p(y,s;x,t-\Delta t) - p(y,s;x,t)] \int^{\infty}_{-\infty} p(z,t;x,t-\Delta t)dz\\
&=\textstyle \int^{\infty}_{-\infty} p(z,t;x,t-\Delta t)[p(y,s;z,t) - p(y,s;x,t)] dz\\
&=\textstyle \int^{\infty}_{-\infty} p(z,t;x,t-\Delta t)\Big[ (z-x) \frac{\partial p(y,s;x,t)}{\partial x} + \frac{(z-x)^2}{2} \frac{\partial^2 p(y,s;x,t)}{\partial x^2} + O( (z-x)^3 ) \Big]
\end{align}](/mediawiki/images/math/8/8/c/88c4ec7817fe002d93f3e6dab9dec02a.png)
![\textstyle \frac{\partial p}{\partial t} = - \alpha \frac{\partial [xp]}{\partial x} + \frac{\beta^2}{2} \frac{\partial^2(xp)}{\partial x^2} \ \ x \in (0, \infty)](/mediawiki/images/math/6/2/f/62fdf8eff011f42ba576d244d83c7290.png)