Aritalab:Lecture/NetworkBiology/Contact Process
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
コンタクトプロセス
感染症モデルでネットワーク構造を考慮したものをコンタクトプロセスと呼ぶ。 それぞれの状態の割合を
- S susceptible (健康状態)
- I infected (感染状態)
- R recovered (治癒状態)
と書く。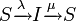 の場合をSISモデルと呼び、
の場合をSISモデルと呼び、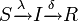 の場合をSIRモデルと呼ぶ。
の場合をSIRモデルと呼ぶ。
SIS model
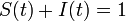
ネットワークを考慮しない場合
時間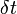 の間に感染者は
の間に感染者は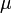 の確率で治癒し、健康人が
の確率で治癒し、健康人が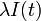 の確率で感染するとする。
の確率で感染するとする。
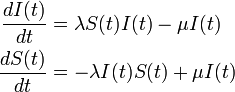
十分時間が経過した後の定常状態を考えると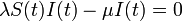 を式変形して
を式変形して
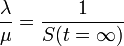
つまり感染率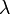 が治癒率
が治癒率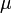 を超える場合は健康人の割合が減少し(病人が必ず残る)、感染率のほうが小さい場合は
を超える場合は健康人の割合が減少し(病人が必ず残る)、感染率のほうが小さい場合は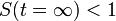 のために病人はゼロになる。
のために病人はゼロになる。
また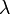 と
と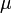 は定数倍すれば片方を消せるので、今後は一般性を失わずに
は定数倍すれば片方を消せるので、今後は一般性を失わずに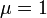 とおく。
とおく。
一般のネットワークの場合
次数分布のみを考慮することにし、前出の式を次数kに限定して考える。
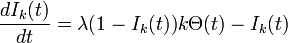
ここで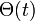 は、次数kの健康人が接続する先(1本あたり)が感染者である期待値を示す。定常状態のとき、
は、次数kの健康人が接続する先(1本あたり)が感染者である期待値を示す。定常状態のとき、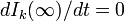 であるから
であるから
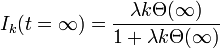
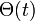 は、次数kの頂点から出る辺が接続する先が感染者である確率を示していた。
辺が接続する先の頂点の次数分布は
は、次数kの頂点から出る辺が接続する先が感染者である確率を示していた。
辺が接続する先の頂点の次数分布は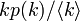 であるから
であるから
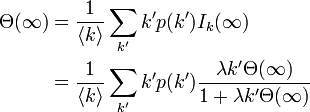
これを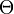 について閉じた式にできれば感染率
について閉じた式にできれば感染率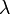 に対する感染者の期待値を解析的に求められるが、それは容易ではない。ここで求めたいのは臨界値を与える
に対する感染者の期待値を解析的に求められるが、それは容易ではない。ここで求めたいのは臨界値を与える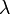 だと考えて、右辺と左辺の関係を考える。
だと考えて、右辺と左辺の関係を考える。
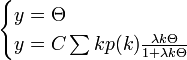
という連立方程式の解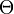 を考えよう。下の曲線は
を考えよう。下の曲線は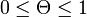 で定義され、
で定義され、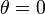 が解の一つである。また
が解の一つである。また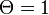 のときに
のときに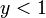 となり単調増加でもある。
となり単調増加でもある。
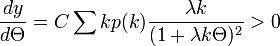
よって連立方程式が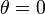 以外にも解を持つかどうかの分岐点は
以外にも解を持つかどうかの分岐点は
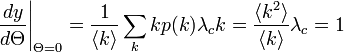
ここから、臨界確率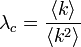 となる。
となる。
SIRモデル
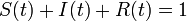
ネットワークを考慮しない場合
時間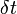 の間に感染者は
の間に感染者は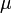 の確率で治癒し、健康人が
の確率で治癒し、健康人が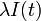 の確率で感染するとする。
の確率で感染するとする。
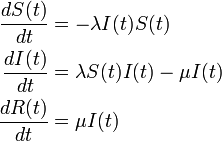
十分時間が経過した後の定常状態において十分量の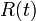 が生じるためには
が生じるためには
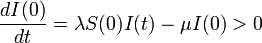
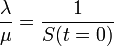
つまり感染率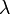 が治癒率
が治癒率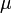 を超える場合は病人の割合が増加する。逆の場合は病人が減少する一方になる。
を超える場合は病人の割合が増加する。逆の場合は病人が減少する一方になる。
SISモデルと同様、今後は一般性を失わずに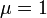 とおく。
とおく。
一般のネットワークの場合
次数分布のみを考慮することにし、前出の式を次数$k$に限定して考える。
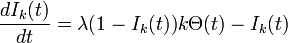
SISモデルとの違いは、いちど感染した頂点がSに戻らずRになる点である。 よって
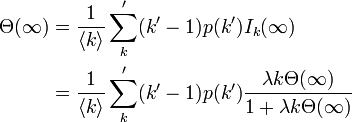
k' が1少なくなっている理由はSに隣接する頂点がIの場合、その頂点を感染させた頂点はIかRであり、二度と感染しないからである。
この式が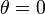 以外にも解を持つかどうかの分岐点は
以外にも解を持つかどうかの分岐点は
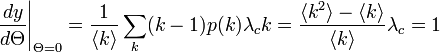
ここから、臨界確率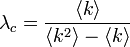 となる。SISモデルとSIRモデルは基本的に結果が変わらない。
となる。SISモデルとSIRモデルは基本的に結果が変わらない。
SIRモデルとパーコレーション
SIRモデルはいったん感染すると後はRに移動するだけである。したがって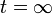 における最終結果は各辺について一回ずつ感染か非感染かを評価するパーコレーションと変わらない。
における最終結果は各辺について一回ずつ感染か非感染かを評価するパーコレーションと変わらない。
このように、頂点ではなく辺に活性、非活性を割り当てる方式をボンド・パーコレーションと呼ぶ。