Aritalab:Lecture/NetworkBiology/Contact Process
(→具体例) |
|||
| Line 8: | Line 8: | ||
:I infected (感染状態) | :I infected (感染状態) | ||
:R recovered (治癒状態) | :R recovered (治癒状態) | ||
| − | + | とします。<math>S \xrightarrow{\lambda}I \xrightarrow{\mu} S</math>の場合をSISモデルと呼び、<math>S \xrightarrow{\lambda} I \xrightarrow{\mu} R</math>の場合をSIRモデルと呼びます。 | |
==SIS model== | ==SIS model== | ||
| Line 16: | Line 16: | ||
===ネットワークを考慮しない場合=== | ===ネットワークを考慮しない場合=== | ||
| − | 時間<math>\delta t</math>の間に感染者は治癒率 <math>\mu</math> で治癒し、健康人が感染率 <math>\lambda\ I(t)</math> で感染するとします。 | + | 時間 <math>\delta t</math> の間に感染者は治癒率 <math>\mu</math> で治癒し、健康人が感染率 <math>\lambda\ I(t)</math> で感染するとします。 |
<math> | <math> | ||
| Line 25: | Line 25: | ||
</math> | </math> | ||
| − | 十分時間が経過した後の定常状態を考えると<math>\textstyle \lambda S(t) I(t) - \mu I(t) = 0</math>を式変形して | + | 十分時間が経過した後の定常状態を考えると <math>\textstyle \lambda S(t) I(t) - \mu I(t) = 0</math> を式変形して |
<math> | <math> | ||
| Line 31: | Line 31: | ||
</math> | </math> | ||
| − | つまり感染率<math>\lambda</math>が治癒率<math>\mu</math>を超える場合は健康人の割合が減少し(病人が必ず残る)、感染率のほうが小さい場合は<math>S(t= \infty) | + | つまり感染率 <math>\lambda</math> が治癒率 <math>\mu</math> を超える場合は健康人の割合が減少し(病人が必ず残る)、感染率のほうが小さい場合は <math>S(t= \infty) \leq 1</math> のため病人はゼロになります。 |
感染症が蔓延するか否かの分かれ目(臨界値)は、個々人の平均的な治癒率よりも感染力が強いかどうかに依存します。 | 感染症が蔓延するか否かの分かれ目(臨界値)は、個々人の平均的な治癒率よりも感染力が強いかどうかに依存します。 | ||
| − | 以降、<math>\lambda</math>と<math>\mu</math>は定数倍(正規化)すれば片方を消せるので、一般性を失わずに<math>\mu=1</math>とおきます。 | + | 以降、<math>\lambda</math> と <math>\mu</math> は定数倍(正規化)すれば片方を消せるので、一般性を失わずに <math>\mu = 1</math> とおきます。 |
===一般のネットワークの場合=== | ===一般のネットワークの場合=== | ||
| Line 44: | Line 44: | ||
</math> | </math> | ||
| − | ここで<math>\Theta(t)\ </math>は、辺の接続先に感染者がいる期待値です。定常状態のとき、<math>d I_k(\infty) / dt =0</math>なので感染者の割合は | + | ここで <math>\Theta(t)\ </math> は、辺の接続先に感染者がいる期待値です。定常状態のとき、<math>d I_k(\infty) / dt =0</math> なので感染者の割合は |
<math> | <math> | ||
| Line 51: | Line 51: | ||
ここで、定常状態における <math>\Theta(\infty)\ </math> を求めましょう。 | ここで、定常状態における <math>\Theta(\infty)\ </math> を求めましょう。 | ||
| − | 次数 ''k'' の頂点から出る辺の先にある頂点の次数分布は<math>k p(k)/\langle k \rangle</math>ですから | + | 次数 ''k'' の頂点から出る辺の先にある頂点の次数分布は <math>k p(k)/\langle k \rangle</math> ですから |
<math>\textstyle | <math>\textstyle | ||
| Line 69: | Line 69: | ||
</math> | </math> | ||
| − | という連立方程式の解<math>\Theta\ </math> | + | という連立方程式の解 <math>\Theta\ </math> を考えます。''C'' は定数です。<math>y_2\ </math> の曲線は <math>0 \leq \Theta \leq 1</math> で定義され、<math>\Theta = 0 |
| − | \ </math> | + | \ </math>が解の一つです。これは感染者 I が 0 の場合に相当します。また <math>\Theta = 1\ </math> のときに <math>y_2 < 1\ </math>です。微分するとその値は正、つまり単調増加です。 |
<math> | <math> | ||
| Line 76: | Line 76: | ||
</math> | </math> | ||
| − | この曲線と、<math> y_1 = \Theta\ </math> | + | この曲線と、<math> y_1 = \Theta\ </math> という曲線の交点が0以外に存在する場合、それがもう一つの解になります。 |
| − | 連立方程式が<math>\ | + | 連立方程式が <math>\Theta = 0</math> 以外にも解を持つかどうかの分岐点は <math>\Theta = 0\ </math>における微分値(傾き)が 1 以上になるかどうかです。 |
<math> | <math> | ||
| Line 83: | Line 83: | ||
</math> | </math> | ||
| − | ここから、臨界確率<math>\lambda_c = \frac{\langle k \rangle}{\langle k^2 \rangle}</math> | + | ここから、臨界確率<math>\lambda_c = \frac{\langle k \rangle}{\langle k^2 \rangle}</math>が導かれます。臨界確率を超えると、<math>1 > \Theta \ > 0</math> で定常状態になる、つまり I が一定率でネットワーク上に残ります。 |
===具体例=== | ===具体例=== | ||
| Line 105: | Line 105: | ||
<math>S(t) + I(t) + R(t) = 1\ </math> が成立します。 | <math>S(t) + I(t) + R(t) = 1\ </math> が成立します。 | ||
| + | SISモデルとの違いは、いちど感染した頂点が S に戻らず R になる点です。 | ||
| + | 実際の感染症でも免疫によって同じ病気には罹りにくくなるので、パラメータが増えますが現実的なモデルといえます。 | ||
| + | 明らかに、SISモデルの感染力 > SIRモデルの感染力です。 | ||
===ネットワークを考慮しない場合=== | ===ネットワークを考慮しない場合=== | ||
| Line 117: | Line 120: | ||
</math> | </math> | ||
| − | + | 十分時間が経過した後の定常状態で I は存在しません。十分量の R が生じるためには、初期に少なかった I が増え、その後終息して R に変化しないといけません。 | |
<math> | <math> | ||
| − | \frac{d I( | + | \frac{d I(t)}{dt} = \lambda S(t) I(t) - \mu I(t) = 0 |
</math> | </math> | ||
| − | + | この式から導かれる | |
<math> | <math> | ||
| − | \frac{\lambda}{\mu} = \frac{1}{S(t | + | \frac{\lambda}{\mu} = \frac{1}{S(t)} |
</math> | </math> | ||
| − | + | という閾値はSISモデルに同じく重要です。つまり感染率 <math>\lambda</math> が治癒率 <math>\mu</math> を超える場合は病人の割合が増加し、逆の場合は病人が減少する一方になります。 | |
| + | 十分時間が経過したあとは | ||
| − | + | <math> | |
| + | \frac{\lambda}{\mu} = \frac{1}{S(\infty)} = \frac{1}{1 - R(\infty)} | ||
| + | </math> | ||
| + | |||
| + | が成立します。定常状態なら <math>I(\infty) = 0</math> であることに注意します。SISモデルと同様、今後は一般性を失わずに<math>\mu=1</math>とおきます。 | ||
===一般のネットワークの場合=== | ===一般のネットワークの場合=== | ||
| Line 138: | Line 146: | ||
<math> | <math> | ||
| − | \frac{d I_k(t)}{dt} = \lambda | + | \frac{d I_k(t)}{dt} = \lambda [1-I_k(t) - R_k(t)] k\Theta(t) - I_k(t) |
</math> | </math> | ||
| − | + | S に隣接する頂点が I である割合を考えましょう。SIRモデルでは <math> I(\infty) = 0 </math> ですが、それまでに I は増減を繰り返すので | |
| − | + | <math>\frac{d I_k(t)}{dt} = 0</math> の状態における <math> \Theta\ </math> を考えましょう。 | |
| − | + | SISモデルに同じく次数 ''k'' の頂点 S に隣接する頂点の次数分布は <math>kp(k)/\langle k \rangle\ </math> であり、S に隣接する I の値を見積もる関数が <math> \Theta\ </math> です。SIRモデルでは I の周囲に少なくとも 1 本は(感染源に対応して)I または R があり、この点は必ず R になるのでネットワークから除外して考えることが可能です。これを大雑把に <math>(k-1)p(k)/\langle k \rangle\ </math>と見積もります。(その差が次数1個分という論理的な必然性はありません。少なくとも 1 点は I か R であるという仮定です。) | |
| − | + | ||
| − | + | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | \Theta( | + | \Theta(t) &= \frac{1}{\langle k \rangle} \sum_j (j-1) p(j) I_j (\infty) \\ |
| − | &= \frac{1}{\langle k \rangle} \sum_j (j-1) p(j) \frac{\lambda | + | &= \frac{1}{\langle k \rangle} \sum_j (j-1) p(j) \frac{\lambda j \Theta(t) (1 - R_j(t))}{1 + \lambda j \Theta(t)} |
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | この式が<math>\ | + | この式が<math>\Theta = 0</math>以外にも解を持つかどうかの分岐点は |
<math> | <math> | ||
| − | \frac{d y}{d \Theta} \Bigg|_{\Theta=0} = \frac{1}{\langle k \rangle} \sum_k (k-1)p(k)\lambda_c k = \frac{\langle k^2 \rangle - \langle k \rangle}{\langle k \rangle}\lambda_c = 1 | + | \frac{d y}{d \Theta} \Bigg|_{\Theta=0} = \frac{1}{\langle k \rangle} \sum_k (k-1)p(k)\lambda_c k (1-R_k(0))= \frac{\langle k^2 \rangle - \langle k \rangle}{\langle k \rangle}\lambda_c = 1 |
</math> | </math> | ||
| + | ここで <math>\Theta\ = 0</math> の場合として <math> t = 0,\ R_k(0) = 0 </math> という条件を利用しました。 | ||
ここから、臨界確率<math>\lambda_c = \frac{\langle k \rangle}{\langle k^2 \rangle - \langle k \rangle}</math>となります。 | ここから、臨界確率<math>\lambda_c = \frac{\langle k \rangle}{\langle k^2 \rangle - \langle k \rangle}</math>となります。 | ||
つまり、SISモデルとSIRモデルは基本的に結果が変わりません。 | つまり、SISモデルとSIRモデルは基本的に結果が変わりません。 | ||
Revision as of 13:31, 24 June 2011
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
コンタクトプロセス
感染症モデルでネットワーク構造を考慮したものをコンタクトプロセスと呼びます。 それぞれの状態の割合を
- S susceptible (健康状態)
- I infected (感染状態)
- R recovered (治癒状態)
とします。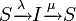 の場合をSISモデルと呼び、
の場合をSISモデルと呼び、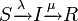 の場合をSIRモデルと呼びます。
の場合をSIRモデルと呼びます。
SIS model
感染者 (infected) の割合を 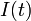 , 健康人 (susceptible) の割合を
, 健康人 (susceptible) の割合を 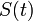 で表します。
で表します。
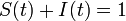
ネットワークを考慮しない場合
時間 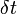 の間に感染者は治癒率
の間に感染者は治癒率 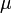 で治癒し、健康人が感染率
で治癒し、健康人が感染率 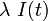 で感染するとします。
で感染するとします。
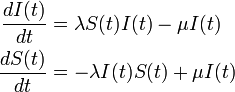
十分時間が経過した後の定常状態を考えると 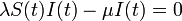 を式変形して
を式変形して
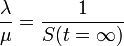
つまり感染率 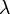 が治癒率
が治癒率 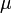 を超える場合は健康人の割合が減少し(病人が必ず残る)、感染率のほうが小さい場合は
を超える場合は健康人の割合が減少し(病人が必ず残る)、感染率のほうが小さい場合は 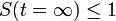 のため病人はゼロになります。
感染症が蔓延するか否かの分かれ目(臨界値)は、個々人の平均的な治癒率よりも感染力が強いかどうかに依存します。
のため病人はゼロになります。
感染症が蔓延するか否かの分かれ目(臨界値)は、個々人の平均的な治癒率よりも感染力が強いかどうかに依存します。
以降、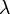 と
と 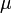 は定数倍(正規化)すれば片方を消せるので、一般性を失わずに
は定数倍(正規化)すれば片方を消せるので、一般性を失わずに 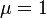 とおきます。
とおきます。
一般のネットワークの場合
次数分布のみを考慮することにし、前出の式を次数 k に限定して考えましょう。次数 k の頂点たちの中における感染者数は
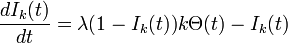
ここで 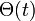 は、辺の接続先に感染者がいる期待値です。定常状態のとき、
は、辺の接続先に感染者がいる期待値です。定常状態のとき、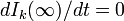 なので感染者の割合は
なので感染者の割合は
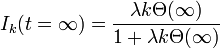
ここで、定常状態における 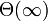 を求めましょう。
次数 k の頂点から出る辺の先にある頂点の次数分布は
を求めましょう。
次数 k の頂点から出る辺の先にある頂点の次数分布は 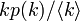 ですから
ですから
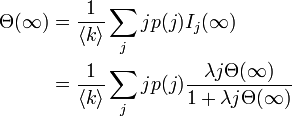
これを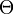 について閉じた式にできれば感染率
について閉じた式にできれば感染率 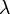 に対する感染者の期待値を解析的に求められますが、容易ではありません。ここで求めたいのは臨界値を与える
に対する感染者の期待値を解析的に求められますが、容易ではありません。ここで求めたいのは臨界値を与える 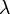 だと考えて、右辺と左辺の関係に注目します。
だと考えて、右辺と左辺の関係に注目します。
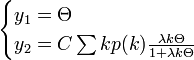
という連立方程式の解 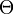 を考えます。C は定数です。
を考えます。C は定数です。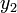 の曲線は
の曲線は 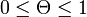 で定義され、
で定義され、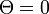 が解の一つです。これは感染者 I が 0 の場合に相当します。また
が解の一つです。これは感染者 I が 0 の場合に相当します。また 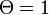 のときに
のときに 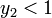 です。微分するとその値は正、つまり単調増加です。
です。微分するとその値は正、つまり単調増加です。
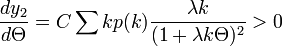
この曲線と、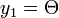 という曲線の交点が0以外に存在する場合、それがもう一つの解になります。
連立方程式が
という曲線の交点が0以外に存在する場合、それがもう一つの解になります。
連立方程式が 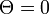 以外にも解を持つかどうかの分岐点は
以外にも解を持つかどうかの分岐点は 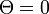 における微分値(傾き)が 1 以上になるかどうかです。
における微分値(傾き)が 1 以上になるかどうかです。
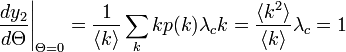
ここから、臨界確率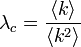 が導かれます。臨界確率を超えると、
が導かれます。臨界確率を超えると、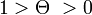 で定常状態になる、つまり I が一定率でネットワーク上に残ります。
で定常状態になる、つまり I が一定率でネットワーク上に残ります。
具体例
- 次数が一定の場合
次数が一定の場合は 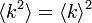 であることに注意すれば
であることに注意すれば 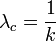 となります。
となります。
- 次数分布がポアソン分布の場合
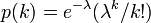 のとき
のとき
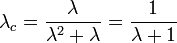
- 次数分布が指数分布の場合
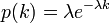 のとき
のとき
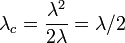
- 次数分布がべき分布の場合
グラフ上のパーコレーションと同じになります(ここを参照)。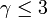 のときに
のときに 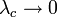 となり、必ず蔓延します。
となり、必ず蔓延します。
SIR model
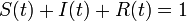 が成立します。
SISモデルとの違いは、いちど感染した頂点が S に戻らず R になる点です。
実際の感染症でも免疫によって同じ病気には罹りにくくなるので、パラメータが増えますが現実的なモデルといえます。
明らかに、SISモデルの感染力 > SIRモデルの感染力です。
が成立します。
SISモデルとの違いは、いちど感染した頂点が S に戻らず R になる点です。
実際の感染症でも免疫によって同じ病気には罹りにくくなるので、パラメータが増えますが現実的なモデルといえます。
明らかに、SISモデルの感染力 > SIRモデルの感染力です。
ネットワークを考慮しない場合
時間 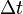 の間に感染者は
の間に感染者は 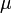 の確率で治癒し、健康人が
の確率で治癒し、健康人が 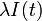 の確率で感染するとします。
の確率で感染するとします。
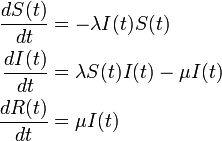
十分時間が経過した後の定常状態で I は存在しません。十分量の R が生じるためには、初期に少なかった I が増え、その後終息して R に変化しないといけません。
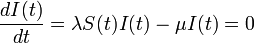
この式から導かれる
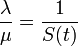
という閾値はSISモデルに同じく重要です。つまり感染率 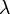 が治癒率
が治癒率 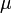 を超える場合は病人の割合が増加し、逆の場合は病人が減少する一方になります。
十分時間が経過したあとは
を超える場合は病人の割合が増加し、逆の場合は病人が減少する一方になります。
十分時間が経過したあとは
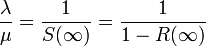
が成立します。定常状態なら 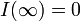 であることに注意します。SISモデルと同様、今後は一般性を失わずに
であることに注意します。SISモデルと同様、今後は一般性を失わずに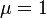 とおきます。
とおきます。
一般のネットワークの場合
次数分布のみを考慮することにし、前出の式を次数 k に限定して考えます。
![\frac{d I_k(t)}{dt} = \lambda [1-I_k(t) - R_k(t)] k\Theta(t) - I_k(t)](/mediawiki/images/math/f/4/7/f474ec8f5cda81ee538f6023fc917e08.png)
S に隣接する頂点が I である割合を考えましょう。SIRモデルでは 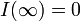 ですが、それまでに I は増減を繰り返すので
ですが、それまでに I は増減を繰り返すので
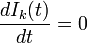 の状態における
の状態における 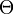 を考えましょう。
SISモデルに同じく次数 k の頂点 S に隣接する頂点の次数分布は
を考えましょう。
SISモデルに同じく次数 k の頂点 S に隣接する頂点の次数分布は 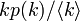 であり、S に隣接する I の値を見積もる関数が
であり、S に隣接する I の値を見積もる関数が 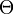 です。SIRモデルでは I の周囲に少なくとも 1 本は(感染源に対応して)I または R があり、この点は必ず R になるのでネットワークから除外して考えることが可能です。これを大雑把に
です。SIRモデルでは I の周囲に少なくとも 1 本は(感染源に対応して)I または R があり、この点は必ず R になるのでネットワークから除外して考えることが可能です。これを大雑把に 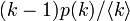 と見積もります。(その差が次数1個分という論理的な必然性はありません。少なくとも 1 点は I か R であるという仮定です。)
と見積もります。(その差が次数1個分という論理的な必然性はありません。少なくとも 1 点は I か R であるという仮定です。)
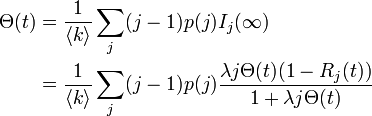
この式が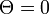 以外にも解を持つかどうかの分岐点は
以外にも解を持つかどうかの分岐点は
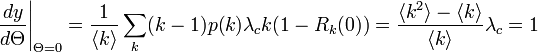
ここで 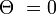 の場合として
の場合として 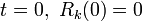 という条件を利用しました。
ここから、臨界確率
という条件を利用しました。
ここから、臨界確率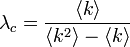 となります。
つまり、SISモデルとSIRモデルは基本的に結果が変わりません。
となります。
つまり、SISモデルとSIRモデルは基本的に結果が変わりません。
SIRモデルとパーコレーション
SIRモデルはいったん感染すると後は R に移動するだけです。したがって 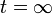 における最終結果は各辺について一回ずつ感染か非感染かを評価するパーコレーションと変わりません。
における最終結果は各辺について一回ずつ感染か非感染かを評価するパーコレーションと変わりません。
このように、頂点ではなく辺に活性、非活性を割り当てる方式をボンド・パーコレーションと呼びます。