Aritalab:Lecture/NetworkBiology/Barabasi-Albert Model
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
Barabási-Albert Model
ネットワークの成長モデルとしてBarabási, Albertは以下のモデルを提唱した。(正確には初期条件が異なるが本質は同じ。)
- 時間ステップ1において
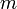 本の辺で結ばれた2頂点からスタートする。
本の辺で結ばれた2頂点からスタートする。
- 単位時間毎に頂点を1つずつ追加し、既に存在する頂点と
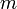 本の辺でつなぐ。新しい辺はそれぞれ確率
本の辺でつなぐ。新しい辺はそれぞれ確率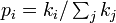 (ここで
(ここで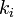 は頂点iの次数) で接続先を決定する。
は頂点iの次数) で接続先を決定する。
このメカニズムを優先的選択(preferential attachment)と呼び、一般にrich gets richerメカニズムなどともいわれる。さらにBarabásiは、グラフの次数分布がべき則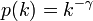 に従う場合をスケールフリー(scale free)ネットワークと呼びはじめた。
に従う場合をスケールフリー(scale free)ネットワークと呼びはじめた。
自然界にはべき則が普通に見られ、以下の例がよく知られている。
| Network (size) | 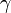 |
L | C | |
|---|---|---|---|---|
| www (1.5 x 105) | 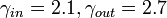 |
3.1 | 0.11 | Barabasi and Albert (1999) |
| Internet (3000-6000) | 2.16 | 3.7 | 0.18-0.3 | Faloutous et al. (1999) |
| Movie actor (2.2 x 105) | 2.3 | 3.7 | 0.79 | Watts and Strogatz (1998) |
| Medline (1.5 x 106) | ? | 4.6 | 0.066 | Newman (2000, 2001) |
べき分布と優先的選択は20世紀初頭にYule、20世紀半ばにもSimonらにより研究されていたが、グラフの次数分布として問題を捉えなおし、WWW等に応用した点が注目された。
べき則のパラメータ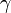 について
について
BAモデルからは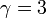 を簡単に導出できる。
初期条件として2頂点が
を簡単に導出できる。
初期条件として2頂点が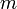 本のリンクで結ばれている場合、
本のリンクで結ばれている場合、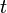 時間後には頂点数
時間後には頂点数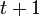 、辺数
、辺数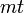 になる。
次数
になる。
次数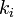 は時間が経つと増加していくから、
は時間が経つと増加していくから、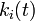 という連続関数として考えてみる。
という連続関数として考えてみる。
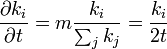
これを解くと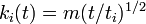 、
ただし
、
ただし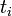 は頂点
は頂点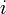 が追加された時間で
が追加された時間で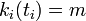 である。
これを式変形すれば、頂点の次数がある値
である。
これを式変形すれば、頂点の次数がある値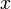 になる時間は
になる時間は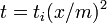 であることがわかる。
次数分布を求めるには、まず頂点の次数が
であることがわかる。
次数分布を求めるには、まず頂点の次数が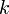 より大きくなる割合(累積分布関数)を求める。
より大きくなる割合(累積分布関数)を求める。
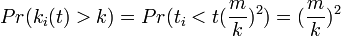
左の等号は、頂点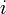 が生まれた時間
が生まれた時間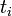 が、時刻
が、時刻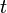 に比例値として
に比例値として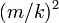 をかけたものよりも早ければ(小さければ)、次数が
をかけたものよりも早ければ(小さければ)、次数が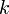 より大きくなることを示している。
しかし頂点が毎時一定量ずつ追加されることを考えると、全体サイズを1とするなら、単純に
より大きくなることを示している。
しかし頂点が毎時一定量ずつ追加されることを考えると、全体サイズを1とするなら、単純に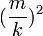 としてよいことがわかる。
としてよいことがわかる。
これを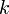 について微分すると
について微分すると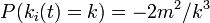 。すなわち辺の次数は
。すなわち辺の次数は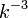 に比例する。
に比例する。
優先的選択でない場合
新しい辺が結びつく先が一様分布に従うと仮定してみよう。
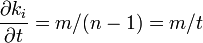
これを解いて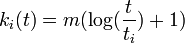 。こちらも累積分布関数を計算してみる。
。こちらも累積分布関数を計算してみる。
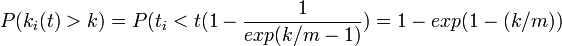
これを微分すると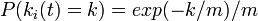 、すなわち辺の次数は指数的に減少することになる。
、すなわち辺の次数は指数的に減少することになる。
何がべき分布を作るのか
エッセンスだけ言うと、優先的選択の場合は次数の時間変化を規定する微分方程式が
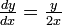 と、
と、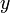 が微分値の分子に現れていた点がミソになる。これを解くと
が微分値の分子に現れていた点がミソになる。これを解くと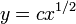 という答えが得られ(
という答えが得られ( は適当な定数)、この係数1/2が
は適当な定数)、この係数1/2が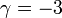 を作り出す。だから異なる
を作り出す。だから異なる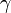 の値を作り出すには
の値を作り出すには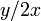 における比の2を他にずらせればよい。
における比の2を他にずらせればよい。
例えば
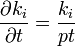
という近似を何らかの形で導出すると、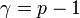 に設定できる。
に設定できる。