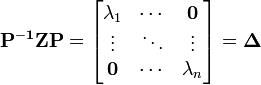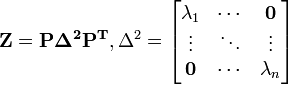Aritalab:Lecture/Math/PCA
m |
m |
||
| Line 3: | Line 3: | ||
主成分分析は行列の特異値分解を利用した手法です。 | 主成分分析は行列の特異値分解を利用した手法です。 | ||
:<b> X = U Δ V<sup>T</sup> = S V<sup>T</sup></b> | :<b> X = U Δ V<sup>T</sup> = S V<sup>T</sup></b> | ||
| − | + | Δは対角成分に特異値(これから説明)が並んだ行列です。 | |
ここで、行列 <b>S (= U Δ)</b> をスコア、<b>V<sup>T</sup></b> をローディング(固有ベクトルに対応)と呼びます。 | ここで、行列 <b>S (= U Δ)</b> をスコア、<b>V<sup>T</sup></b> をローディング(固有ベクトルに対応)と呼びます。 | ||
| Line 12: | Line 12: | ||
各主成分軸は元々の説明変数を線形結合して得られますが、各軸が直交するように設定されるため共線性の問題を回避できます。 | 各主成分軸は元々の説明変数を線形結合して得られますが、各軸が直交するように設定されるため共線性の問題を回避できます。 | ||
;[[Aritalab:Lecture/Math/PCA/R_PCA|RによるPCA実習]] | ;[[Aritalab:Lecture/Math/PCA/R_PCA|RによるPCA実習]] | ||
| + | |||
| + | |||
| + | ==スペクトル分解、特異値分解== | ||
| + | |||
| + | n x n の正方行列 <b>Z</b> が逆行列を持つ場合(つまり正則のとき)、固有値 λ<sub>1</sub> ... λ<sub>n</sub> とその固有ベクトル <b> P </b> = [ x<sub>1</sub> ... x<sub>n</sub> ] を用いて行列を対角化できます。 | ||
| + | : <math> \mathbf{P^{-1} Z P } = \begin{bmatrix}\textstyle \lambda_1 & \cdots & \mathbf{0} \\ \vdots & \ddots & \vdots \\ \mathbf{0} & \cdots & \lambda_n \end{bmatrix} = \mathbf{\Delta}</math> | ||
| + | これは <b> Z = P Δ P<sup>-1</sup></b> と一意に分解できることを意味します。さらに行列 <b>Z</b> が対称行列の場合、固有値 λ は全て実数になります。 | ||
| + | |||
| + | 普通、我々が扱う行列は正方でも正則でもない場合が多いのですが、自分自身の転置と掛けあわせることで対称行列にできます。そして <b>Z = A<sup>T</sup> A</b> と表される正方行列 <b>Z</b> の固有値は常に正またはゼロとなります。さらに固有ベクトルも直交します。 | ||
| + | |||
| + | <b>A</b> が n x p 行列の場合 ( p ≦ n )、<b>A<sup>T</sup> A</b> という p x p 行列と <b>A A<sup>T</sup></b> という n x n 行列が考えられます。どちらも対称行列で、両者のランクと固有値は一致します(つまり大きな n x n 行列のほうはゼロ固有値が多いということ)。 | ||
| + | {{Twocolumn| | ||
| + | 対称行列 <b>Z</b> が異なる n 個の固有値を持つ場合、対応する固有ベクトルを P とすると | ||
| + | : <math> \mathbf{Z = P \Delta^2 P^{T} }, \Delta^2 = \begin{bmatrix}\textstyle \lambda_1 & \cdots & \mathbf{0} \\ \vdots & \ddots & \vdots \\ \mathbf{0} & \cdots & \lambda_n \end{bmatrix}</math> | ||
| + | が成立します。これをスペクトル分解といいます。 | ||
| + | | | ||
| + | [[Image:Lecture_Math_PCA_Spectral.png|right|300px]] | ||
| + | }} | ||
| + | |||
| + | n x p の行列 <b>A</b> が与えられたとき | ||
| + | :<b> A A<sup>T</sup> = U Δ<sup>2</sup> U<sup>T</sup></b> | ||
| + | :<b> A<sup>T</sup> A = V Δ<sup>2</sup> V<sup>T</sup></b> | ||
| + | という二通りのスペクトル分解ができることをみてきました。ここで <b>U, V</b> はそれぞれ n x k 行列、 p x k 行列です。 | ||
Revision as of 12:59, 4 June 2013
主成分分析
主成分分析は行列の特異値分解を利用した手法です。
- X = U Δ VT = S VT
Δは対角成分に特異値(これから説明)が並んだ行列です。 ここで、行列 S (= U Δ) をスコア、VT をローディング(固有ベクトルに対応)と呼びます。
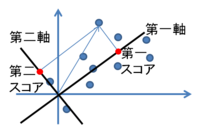
最も大きな固有値に対応する固有ベクトル、つまり元データの分散が最大になる方向を第一軸といいます。第一軸はスコア行列の第一列およびローディング行列の第一行で構成されます。第二軸はスコア行列の第二列とローディング行列の第二行にあたり、第一軸と直交する方向に設定されます。
各主成分軸は元々の説明変数を線形結合して得られますが、各軸が直交するように設定されるため共線性の問題を回避できます。
スペクトル分解、特異値分解
n x n の正方行列 Z が逆行列を持つ場合(つまり正則のとき)、固有値 λ1 ... λn とその固有ベクトル P = [ x1 ... xn ] を用いて行列を対角化できます。
これは Z = P Δ P-1 と一意に分解できることを意味します。さらに行列 Z が対称行列の場合、固有値 λ は全て実数になります。
普通、我々が扱う行列は正方でも正則でもない場合が多いのですが、自分自身の転置と掛けあわせることで対称行列にできます。そして Z = AT A と表される正方行列 Z の固有値は常に正またはゼロとなります。さらに固有ベクトルも直交します。
A が n x p 行列の場合 ( p ≦ n )、AT A という p x p 行列と A AT という n x n 行列が考えられます。どちらも対称行列で、両者のランクと固有値は一致します(つまり大きな n x n 行列のほうはゼロ固有値が多いということ)。
対称行列 Z が異なる n 個の固有値を持つ場合、対応する固有ベクトルを P とすると
n x p の行列 A が与えられたとき
- A AT = U Δ2 UT
- AT A = V Δ2 VT
という二通りのスペクトル分解ができることをみてきました。ここで U, V はそれぞれ n x k 行列、 p x k 行列です。