Aritalab:Lecture/Bioinformatics/Homology
m |
m (→最長共通部分列) |
||
| Line 59: | Line 59: | ||
==最長共通部分列== | ==最長共通部分列== | ||
| − | 配列が与えられた時、共通して現れる部分文字列(連続する必要はない)のうち、最長のものを求めるアルゴリズムを考えてみましょう。これを最長共通部分列 (LCS: longest common | + | 配列が与えられた時、共通して現れる部分文字列(連続する必要はない)のうち、最長のものを求めるアルゴリズムを考えてみましょう。これを最長共通部分列 (LCS: longest common subsequence) と呼びます。 |
ある文字列 s と t を与えられたとき、それらの LCS を LCS(s, t) と書きましょう。 s と t が 1 文字ずつ長くなって、それぞれ sx, ty になったとしましょう(x, y はアルファベット 1 文字)。このとき、以下の等式が成り立ちます。(ちょっとわかりにくいですが、LCS(s,t)x とは s と t の最長共通部分列に x を付加したものを意味しています。) | ある文字列 s と t を与えられたとき、それらの LCS を LCS(s, t) と書きましょう。 s と t が 1 文字ずつ長くなって、それぞれ sx, ty になったとしましょう(x, y はアルファベット 1 文字)。このとき、以下の等式が成り立ちます。(ちょっとわかりにくいですが、LCS(s,t)x とは s と t の最長共通部分列に x を付加したものを意味しています。) | ||
Revision as of 14:38, 13 December 2011
配列の相同性
進化の観点から似ている配列どうしを相同である (homologous) といいます。配列の相同性 (homology) という概念は、単なる類似性 (similarity) とは異なります。進化的に関係なくたまたま似ている場合は、相同であるとは言いません。配列比較をおこなうときに、生物学的に意味のある類似性を見出すことは重要なテーマです。
以下の 2 つのDNA配列 (27塩基) は相同でしょうか?
| g | c | t | a | g | g | a | t | c | a | c | g | g | c | c | a | t | g | g | c | a | a | g | c | g | c | g |
| a | a | t | t | g | a | a | g | g | a | t | t | g | c | t | c | g | g | a | t | a | a | t | c | g | c | c |
2 つの塩基がランダムだとすると、DNA配列は 1/4 の確率で一致し、3/4 の確率で不一致になります。ですから 12 塩基が一致するのはランダムな配列よりも似ているように思えます。ただし、上の揃え方では連続して一致する部分配列は長くても 3 つしか続きません。これを似ていると言ってよいのでしょうか。ここでは、相同性を判断するための様々な「指標」を考えましょう。
配列の組成、GC含量
配列がランダムであるかどうかの単純な指標は、塩基の組成をみることです。例1 の塩基配列組成は以下のようになっています。
|
|
長さが 27 塩基の場合、a, c, g, t のそれぞれは 6 ∼ 8 個ずつありそうなものですが、上の配列は t が 3 個しかありません。これはどのくらいの確率で生じる現象なのでしょうか。話を簡単にするため、gc 含量という概念を使います。塩基配列は常に相補鎖があり、a は t と、g は c と対合しています。ですから単純に t だけの量を議論するのは不正確で、a + t, g + c を比較します。
全部で 27 箇所に、at または gc がランダムに配置されるとき、平均して 13 または 14 箇所が at になると考えられます。では at が 9 箇所にしか現れない確率は、その平均的な場合に比較してどれくらい珍しいのでしょうか。それは二項係数の比を求めればわかります。
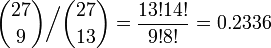
ランダムな配列と大差ないことがわかります。同様の計算で、もし at が 5 箇所にしか出てこない場合は、平均的な場合に比して 0.004 だとわかります。(稀といえるでしょう。)
最長共通部分列
配列が与えられた時、共通して現れる部分文字列(連続する必要はない)のうち、最長のものを求めるアルゴリズムを考えてみましょう。これを最長共通部分列 (LCS: longest common subsequence) と呼びます。
ある文字列 s と t を与えられたとき、それらの LCS を LCS(s, t) と書きましょう。 s と t が 1 文字ずつ長くなって、それぞれ sx, ty になったとしましょう(x, y はアルファベット 1 文字)。このとき、以下の等式が成り立ちます。(ちょっとわかりにくいですが、LCS(s,t)x とは s と t の最長共通部分列に x を付加したものを意味しています。)
LCS (sx, ty) = max( LCS(sx, t), LCS(s, ty), if (x = y) then LCS(s,t)x else LCS(s,t) )
当たり前ですが s, t が長さ 0 の場合、LCS(x,y) = if (x = y) then x else 0 となっています。最後の if then っだけでなく、LCS(sx, t) などが必要な理由は、新しく付け加えた文字 x, y のどちらか片方だけを LCS として使うことを許すためです。
この式が理解できたら、動的計画法 (dynamic programming) という方法を使って LCS を計算できます。例1の文字列から最初の 9 文字だけを取り出して考えましょう。途中計算を書き込む表を用意し、2 本の配列をそれぞれ第 1 行と第 1 列に配置します。この表の各セルに数字を埋めていきますが、数字は文字列の先頭からそのセルの行と列までで構成される部分文字列における LCS の長さを意味します。初期状態として、長さ 0 の文字列における LCS を意味する 0 を埋めてあります。
|
|
|
|
列方向の最初の文字 a と、行方向の文字列の比較を考えてみましょう。行方向の文字列で a が 1 箇所出てくれば、それ以降の文字がなんであっても LCS は 1 になります。つまり LCS(a, gcta) = LCS(a, gctaggatc) = a です。したがって、000011111 と数字を埋めていきます。 列方向に最初の 2 文字 (aa) を考えるとき、行方向の文字列で a が 2 回目に出てくる所で LCS は 2 になります。つまり LCS(aa, gctagga) = aa です。対応する LCS の長さを埋めていくと、数字は 000111222 となります。 列方向に 3 文字を (aat) をとるとき、LCS(aat, gcta) をどう埋めるべきでしょうか。LCS は a または t のどちらでもよく、長さは 1 になります。では LCS(aat, gctaggat) はどうでしょうか。LCS は aat になり 3 です。 各セルの値を埋めるときは、左隣、真上、左上の 3 箇所のセルの値だけをみれば良いことに気づきます。左隣の値、真上の値、それからセルに対応する文字が一致している場合は左上のセルの値 + 1 、そうでない場合は左上のセルの値のうち、最大値をとって埋めていけばよいのです。 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
セルを全部埋めると左のようになります。右下の数字は 4 で、実際に LCS(aattgaagg, gctaggatc) = tagg (or gagg) です。文字列 tagg はどのように求めるのでしょうか。一番右下の数字 4 が生成された経緯をたどればよく、この処理をトレースバック (trace back) といいます。 数字の 4 は、最下段で太字で示したセルで初めて現れました。これは文字 g の一致 (aattgaagg, gctaggatc) に対応します。その左上のセルは 3 で、このセルも同じく g の一致により更に左上のセルから生成されています。4 から左上にたどると agg という文字列の一致 (aattgaagg, gctaggatc) に対応します。太字の数字 2 の左上には 1 がありますが、この値はこのセルで生じたものではありません。左隣か上のセルに由来しています。1 が初めて生じたセルを探すと太字で示した 1 にたどり着きます。このどちらをとっても正解であり、tagg または gagg という LCS を求められます。 |
|