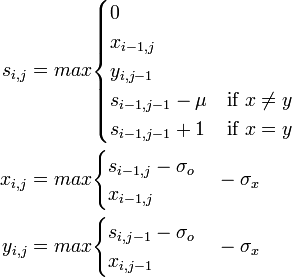Aritalab:Lecture/Bioinformatics/Alignment
m |
|||
| Line 78: | Line 78: | ||
==Smith-Waterman アルゴリズム== | ==Smith-Waterman アルゴリズム== | ||
| − | バイオインフォマティクスの草分けである Temple F. Smith と Michael S. Waterman が 1981 年に Journal of Molecular Biology誌 (147: 195–197) に発表した局所アライメントを求めるアルゴリズムです。MS Waterman は動的計画法を RNA 二次構造の解析などに応用して活躍した数学者ですが、TF Smithは配列アライメントに関する実績もなく、このアルゴリズムをWalther Goad から聞いて論文にしたといわれる曰くつきのアルゴリズムです<ref>Walter Goad は後日 W Goad "Sequence Analysis: Contributions by Ulam to Molecular Genetics" Los Alamos Science (special issue) 288-291, 1987 ([http://library.lanl.gov/cgi-bin/getfile?15-21.pdf pdf]) に、自分のほうが先に見つけたと言いたげな記述をしています。</ref> | + | バイオインフォマティクスの草分けである Temple F. Smith と Michael S. Waterman が 1981 年に Journal of Molecular Biology誌 (147: 195–197) に発表した局所アライメントを求めるアルゴリズムです。MS Waterman は動的計画法を RNA 二次構造の解析などに応用して活躍した数学者ですが、TF Smithは配列アライメントに関する実績もなく、このアルゴリズムをWalther Goad から聞いて論文にしたといわれる曰くつきのアルゴリズムです<ref>Walter Goad は後日 W Goad "Sequence Analysis: Contributions by Ulam to Molecular Genetics" Los Alamos Science (special issue) 288-291, 1987 ([http://library.lanl.gov/cgi-bin/getfile?15-21.pdf pdf]) に、自分のほうが先に見つけたと言いたげな記述をしています。</ref>。FASTAパッケージ(後述)の中では SSEARCH の名前で実装されていました。局所アライメントは以下のように定義されます。 |
<center> | <center> | ||
| Line 93: | Line 93: | ||
ここではギャップペナルティを 2、ミスマッチペナルティを 1 として、2つの配列 gctagg と aattgaagg の間のアライメントを考えてみましょう。スコア行列は右のようになります。 | ここではギャップペナルティを 2、ミスマッチペナルティを 1 として、2つの配列 gctagg と aattgaagg の間のアライメントを考えてみましょう。スコア行列は右のようになります。 | ||
| − | どこからアライメントを初めてもよいため 1 行目と 1 列目はすべて 0 | + | どこからアライメントを初めてもよいため 1 行目と 1 列目はすべて 0 にします<ref>本当は漸化式の中に0を含めるのでどんな正値でも良いのですが、分かりやすさのためにどの本を見ても0で埋めると書いてあります。</ref>。 |
| − | + | 残りのセルは動的計画法に基づいてスコアが埋められ、最適アライメントは以下のようになります。この例は説明の都合上、大域アライメントと同じ配列のため、たまたま右下部分が最大値になっています。アルゴリズム自体は最適値がスコア行列の任意の箇所に出てもよいことに注意してください。 | |
<big><pre> | <big><pre> | ||
7:agg:9 | 7:agg:9 | ||
| Line 147: | Line 147: | ||
|} | |} | ||
|} | |} | ||
| + | |||
| + | ==アフィンギャップと Gotoh アルゴリズム== | ||
| + | |||
| + | 上記のアルゴリズムでは、ギャップとして欠ける塩基数に比例したペナルティが課されますが、これは配列進化の観点では不適切です。 | ||
| + | ギャップとは配列が切断されることを意味しますが、あいだに挿入される(または欠失する)配列の長さはさほど重要ではありません。このため、実用的なアルゴリズムでは | ||
| + | |||
| + | :ギャップ開始 (open) ペナルティ σ<sub>o</sub> | ||
| + | :ギャップ伸長 (extension) ペナルティ σ<sub>x</sub> (この値は開始ペナルティよりもずっと小さくする) | ||
| + | |||
| + | を導入し、長さ n のギャップに対して σ<sub>o</sub> + n σ<sub>x</sub> のコストとします。このペナルティ方式を、ギャップ長に比例する値でコストが増加するため、(平行移動のアフィン変換にちなんで)アフィンギャップコストと呼びます。この関数を使うと、アライメントスコアは | ||
| + | |||
| + | <center> | ||
| + | (マッチ数) − μ(ミスマッチ数) − σ<sub>o</sub>(ギャップ開始数) − σ<sub>x</sub>(ギャップスペース数) | ||
| + | </center> | ||
| + | |||
| + | と書けます。ギャップスペース数に対するペナルティはこれまでのギャップペナルティに同値なので、問題はギャップ開始数の数え方です。 | ||
| + | |||
| + | {| | ||
| + | |valign="top"| | ||
| + | まずスコア行列と同じサイズのギャップ管理用行列 X (横方向用)、Y (縦方向用) を用意します。それらの初期値は位置 (i,0), (0,j) に対してそれぞれ −σ<sub>o</sub> − i σ<sub>x</sub> と −σ<sub>o</sub> − j σ<sub>x</sub> とします。ここでは σ<sub>o</sub> = 2, σ<sub>x</sub> = 0.1 で計算してあります。そして以下の漸化式を用います。 | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | s_{i,j} &= max \begin{cases}0 \\ x_{i-1,j} \\ y_{i,j-1} \\ s_{i-1,j-1} - \mu & \mbox{if } x \ne y \\ s_{i-1,j-1} +1 & \mbox{if } x = y | ||
| + | \end{cases} \\ | ||
| + | x_{i,j} &= max \begin{cases} s_{i-1, j} - \sigma_o \\ x_{i-1,j} \end{cases} - \sigma_x \\ | ||
| + | y_{i,j} &= max \begin{cases} s_{i, j-1} - \sigma_o \\ x_{i,j-1} \end{cases} - \sigma_x \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | |width="50%" valign="top"| | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center" | ||
| + | |+ 初期行列の値(スコア用、ギャップ管理用とも共通) | ||
| + | |- | ||
| + | | | ||
| + | |style="width:3em"| -2.0 | ||
| + | |style="width:3em"| -2.1 | ||
| + | |style="width:3em"| -2.2 | ||
| + | |style="width:3em"| -2.3 | ||
| + | |style="width:3em"| ... | ||
| + | |style="width:3em"| j | ||
| + | |- | ||
| + | | -2.0 || || || || | ||
| + | |rowspan="4"| | ||
| + | |rowspan="4" style="background:lightgray"| | ||
| + | |- | ||
| + | | -2.1 || || || || | ||
| + | |- | ||
| + | | -2.2 || || || || | ||
| + | |- | ||
| + | | : | ||
| + | |- | ||
| + | | i | ||
| + | |colspan="5" style="background:lightgray"| | ||
| + | | s<sub>i, j</sub> | ||
| + | |- | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | 位置 (i, j) にいるとき、スコアの求め方を考えましょう。普通に考えるとセル (i, j) の左側全部と上側全部のセル(影がかかっている領域)全ての位置から、ギャップが入る可能性を検討しなくてはなりません。それを素直に実行すると各セルの値を計算するのに O(n) 時間かかるため、全体で O(n<sup>3</sup>) 時間の計算量になってしまいます。その手間を省くために行列 X, Y を導入したわけです。 | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
;参考文献 | ;参考文献 | ||
<references/> | <references/> | ||
Revision as of 12:00, 15 December 2011
Needleman-Wunsch (-Sellers) アルゴリズム
1970年、分子生物学者の Saul B. NeedlemanとChristian D. Wunsch は、大域アライメントのアルゴリズムを Journal of Molecular Biology誌 (1970) 48: 443-453 に発表しました。いまでは誤って Needleman-Wunsch アルゴリズムと呼ばれるようになりましたが、論文は効率が悪い手法、O(n3) 時間、を紹介しています。ここで紹介されるアルゴリズムの原型を作ったのは Peter Sellers (1974) です[1]。したがって正確には Needleman-Wunsch-Sellers アルゴリズムと呼ぶべきでしょう [2]。
基本は最長共通部分列(LCS)アルゴリズムと同じで、動的計画法によるLCSのページで紹介した以下の漸化式に基づいてスコア行列を計算します。ギャップとミスマッチに対してそれぞれペナルティスコア (gap penalty σ, mismatch penalty δ)が与えられています。
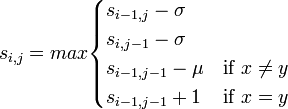
|
ここではギャップペナルティを 2、ミスマッチペナルティを 1 として、2つの配列 gctagg と aattgaagg の間のアライメントを考えてみましょう。スコア行列は右のようになります。 1行目と1列目は 0, -2, -4, -6, ... -18 とギャップペナルティに基づく等差数列ができています。これは左隣(または上)のセルからギャップペナルティ 2 を順次マイナスしてできる部分です。大域アライメントでは配列の最初と最後を揃えるために、初期状態としてギャップの数に比例するペナルティを与えます。 残りのセルは動的計画法に基づいてスコアが埋められ、最適アライメントは以下のようになります。
1:aattgaagg:9
| | ||
1:gct--a-gg:6
右図のトレースバックと見比べてみてください。大域アライメントのスコアは マッチ 4 × 1 + ミスマッチ 2 × (-1) + ギャップ 3 × (-2) = -4 となっています。大域アライメントにおけるギャップの数は配列長の差になります。具体的なアルゴリズムとJavaコードはこのページを参照してください。 |
|
Smith-Waterman アルゴリズム
バイオインフォマティクスの草分けである Temple F. Smith と Michael S. Waterman が 1981 年に Journal of Molecular Biology誌 (147: 195–197) に発表した局所アライメントを求めるアルゴリズムです。MS Waterman は動的計画法を RNA 二次構造の解析などに応用して活躍した数学者ですが、TF Smithは配列アライメントに関する実績もなく、このアルゴリズムをWalther Goad から聞いて論文にしたといわれる曰くつきのアルゴリズムです[3]。FASTAパッケージ(後述)の中では SSEARCH の名前で実装されていました。局所アライメントは以下のように定義されます。
局所アライメント = 与えられた2つの配列それぞれの全ての部分配列のペア中で、大域アライメントのスコアを最大にするもの
すべての部分配列を列挙して大域アライメントを施す必要が思えますが、そうではありません。動的計画法において常にスコア 0 を候補に置くだけで、同じ計算時間で局所アライメントを求められるところが大変エレガントなアルゴリズムです。オリジナル論文はアフィンギャップ関数(後述)という、生物学的に意味のあるギャップペナルティを採用しています。
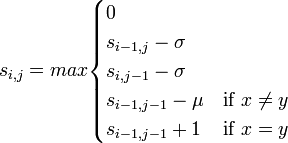
|
ここではギャップペナルティを 2、ミスマッチペナルティを 1 として、2つの配列 gctagg と aattgaagg の間のアライメントを考えてみましょう。スコア行列は右のようになります。 どこからアライメントを初めてもよいため 1 行目と 1 列目はすべて 0 にします[4]。 残りのセルは動的計画法に基づいてスコアが埋められ、最適アライメントは以下のようになります。この例は説明の都合上、大域アライメントと同じ配列のため、たまたま右下部分が最大値になっています。アルゴリズム自体は最適値がスコア行列の任意の箇所に出てもよいことに注意してください。
7:agg:9
|||
4:agg:6
具体的なアルゴリズムとJavaコードはこのページを参照してください。 |
|
アフィンギャップと Gotoh アルゴリズム
上記のアルゴリズムでは、ギャップとして欠ける塩基数に比例したペナルティが課されますが、これは配列進化の観点では不適切です。 ギャップとは配列が切断されることを意味しますが、あいだに挿入される(または欠失する)配列の長さはさほど重要ではありません。このため、実用的なアルゴリズムでは
- ギャップ開始 (open) ペナルティ σo
- ギャップ伸長 (extension) ペナルティ σx (この値は開始ペナルティよりもずっと小さくする)
を導入し、長さ n のギャップに対して σo + n σx のコストとします。このペナルティ方式を、ギャップ長に比例する値でコストが増加するため、(平行移動のアフィン変換にちなんで)アフィンギャップコストと呼びます。この関数を使うと、アライメントスコアは
(マッチ数) − μ(ミスマッチ数) − σo(ギャップ開始数) − σx(ギャップスペース数)
と書けます。ギャップスペース数に対するペナルティはこれまでのギャップペナルティに同値なので、問題はギャップ開始数の数え方です。
|
まずスコア行列と同じサイズのギャップ管理用行列 X (横方向用)、Y (縦方向用) を用意します。それらの初期値は位置 (i,0), (0,j) に対してそれぞれ −σo − i σx と −σo − j σx とします。ここでは σo = 2, σx = 0.1 で計算してあります。そして以下の漸化式を用います。
|
位置 (i, j) にいるとき、スコアの求め方を考えましょう。普通に考えるとセル (i, j) の左側全部と上側全部のセル(影がかかっている領域)全ての位置から、ギャップが入る可能性を検討しなくてはなりません。それを素直に実行すると各セルの値を計算するのに O(n) 時間かかるため、全体で O(n3) 時間の計算量になってしまいます。その手間を省くために行列 X, Y を導入したわけです。 | ||||||||||||||||||||||||||||||||
- 参考文献
- ↑ P Sellers "On the theory and computation of evolutionary distances" SIAM J. Appl. Math. 26:787–793, 1974 にアルゴリズムが紹介されています。
- ↑ 1970年当時の様子は David Sankoff "The early introduction of dynamic programming into computational biology" Bioinformatics 16(1):41-47 (pdf)を見るとよいでしょう。
- ↑ Walter Goad は後日 W Goad "Sequence Analysis: Contributions by Ulam to Molecular Genetics" Los Alamos Science (special issue) 288-291, 1987 (pdf) に、自分のほうが先に見つけたと言いたげな記述をしています。
- ↑ 本当は漸化式の中に0を含めるのでどんな正値でも良いのですが、分かりやすさのためにどの本を見ても0で埋めると書いてあります。