Aritalab:Lecture/Basic/Probability
| Line 1: | Line 1: | ||
{{Probability/Header}} | {{Probability/Header}} | ||
| − | + | ==確率の定義== | |
| − | + | ||
確率を論じるためには | 確率を論じるためには | ||
# 起こりうるすべての事象を含む標本空間 Ω | # 起こりうるすべての事象を含む標本空間 Ω | ||
| Line 13: | Line 12: | ||
を満たさなくてはならず、コルモゴロフの公理と呼ばれています。Pr(''E'') を事象 ''E'' の確率と呼びます。 | を満たさなくてはならず、コルモゴロフの公理と呼ばれています。Pr(''E'') を事象 ''E'' の確率と呼びます。 | ||
| − | + | ==条件付き確率== | |
事象 ''F'' が起こったあとで事象 ''E'' が起きる条件付き確率を | 事象 ''F'' が起こったあとで事象 ''E'' が起きる条件付き確率を | ||
| − | Pr( ''E'' | ''F'' ) = Pr( ''E'' ∩ ''F'') / Pr (''F'') | + | Pr( ''E'' | ''F'' ) = Pr( ''E'' ∩ ''F'' ) / Pr (''F'' ) |
| − | と書きます。''F'' が起こる確率の内訳としての Pr( ''E'' ∩ ''F'') を求めるわけです。もし ''E'' と ''F'' が独立の事象なら Pr( ''E'' | ''F'' ) = Pr (''E'') になります。 | + | と書きます。''F'' が起こる確率の内訳としての Pr( ''E'' ∩ ''F'' ) を求めるわけです。もし ''E'' と ''F'' が独立の事象なら Pr( ''E'' | ''F'' ) = Pr (''E'' ) になります。 |
| − | + | ===全確率の法則=== | |
任意の確率は、互いに背反な事象 <math>\cup^n_{i=1}E_i = \Omega</math> を用いて | 任意の確率は、互いに背反な事象 <math>\cup^n_{i=1}E_i = \Omega</math> を用いて | ||
| Line 27: | Line 26: | ||
と書けます。 | と書けます。 | ||
| − | + | ===ベイズの法則=== | |
互いに背反な事象 <math> \cup^n_{i=1}E_i = E</math> にたいして | 互いに背反な事象 <math> \cup^n_{i=1}E_i = E</math> にたいして | ||
<math>\mbox{Pr}(E_i|B) = \frac{\mbox{Pr}(E_i \cap B)}{\mbox{Pr}(B)} = \frac{\mbox{Pr}(E_i \cap B)}{\sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)} = \frac{\mbox{Pr}(B | E_i)\mbox{Pr}(E_i)}{\sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)}</math> | <math>\mbox{Pr}(E_i|B) = \frac{\mbox{Pr}(E_i \cap B)}{\mbox{Pr}(B)} = \frac{\mbox{Pr}(E_i \cap B)}{\sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)} = \frac{\mbox{Pr}(B | E_i)\mbox{Pr}(E_i)}{\sum^n_{i=1}\mbox{Pr}(B|E_i)\mbox{Pr}(E_i)}</math> | ||
| − | + | 最初と最後のイコールは条件付き確率の定義、次のイコールは全確率の法則です。 | |
| − | + | 事象 E<sub>i</sub> に対して Pr( E<sub>i</sub> ) は事象 B が起こる前に与えられる確率であるから事前確率といい、Pr( E<sub>i</sub> | B ) は B が起こった後で与えられる確率であるから事後確率といいます。 | |
| − | + | ||
| − | 3枚のコインがあり、そのうち1枚だけは表が2/3、残りは1/2の確率で出るとします。''i'' 番目のコインがいかさまである事象を ''E<sub>i</sub>'' | + | ==例== |
| + | ===いかさまコインを見分ける=== | ||
| + | 3枚のコインがあり、そのうち1枚だけは表が2/3、残りは1/2の確率で出るとします。''i'' 番目のコインがいかさまである事象を ''E<sub>i</sub>'' と書きましょう。最初に Pr (''E<sub>i</sub>'' ) = 1/3 ( ''i'' = 1,2,3) とします。 | ||
いま、3枚のコインを順に投げて 表 裏 裏 が出たとします。この事象を ''B'' と書き、''E<sub>i</sub>'' に対する条件付き確率を求めてみます。 | いま、3枚のコインを順に投げて 表 裏 裏 が出たとします。この事象を ''B'' と書き、''E<sub>i</sub>'' に対する条件付き確率を求めてみます。 | ||
| − | :Pr(''B'' | ''E''<sub>1</sub>) = 2/3 × 1/2 × 1/2 = 1/6 | + | :1番目のコインがいかさまの場合 Pr(''B'' | ''E''<sub>1</sub>) = 2/3 × 1/2 × 1/2 = 1/6 |
| − | :Pr(''B'' | ''E''<sub>2</sub>) = 1/2 × 1/3 × 1/2 = 1/12 | + | :2番目のコインがいかさまの場合 Pr(''B'' | ''E''<sub>2</sub>) = 1/2 × 1/3 × 1/2 = 1/12 |
| − | :Pr(''B'' | ''E''<sub>3</sub>) = 1/2 × 1/2 × 1/3 = 1/12 | + | :2番目のコインがいかさまの場合 Pr(''B'' | ''E''<sub>3</sub>) = 1/2 × 1/2 × 1/3 = 1/12 |
| − | :Pr(''B'') = Σ<sub>''i''</sub><sup>3</sup> Pr(B | ''E<sub>i</sub>'') Pr(''E<sub>i</sub>'') = 1/6 * 1/3 + 1/12 * 1/3 + 1/12 * 1/3 = 1/9 | + | :表裏裏を観測する確率 Pr(''B'') = Σ<sub>''i''</sub><sup>3</sup> Pr(B | ''E<sub>i</sub>'') Pr(''E<sub>i</sub>'') = 1/6 * 1/3 + 1/12 * 1/3 + 1/12 * 1/3 = 1/9 |
| − | + | ここでベイズの法則を用います。表裏裏を観測したあとで、各コインがいかさまである確率を求めてみます。 | |
| − | Pr(''E''<sub>1</sub>|B) = Pr(B | ''E''<sub>1</sub>) Pr(''E''<sub>1</sub>) / Pr(''B'') = 1/6 * 1/3 * 9 = 1/2 | + | :1番目のコインがいかさまの場合 Pr(''E''<sub>1</sub> | B) = Pr(B | ''E''<sub>1</sub>) Pr(''E''<sub>1</sub>) / Pr(''B'') = 1/6 * 1/3 * 9 = 1/2 |
| + | :2番目のコインがいかさまの場合 Pr(''E''<sub>2</sub> | B) = Pr(B | ''E''<sub>2</sub>) Pr(''E''<sub>2</sub>) / Pr(''B'') = 1/12 * 1/3 * 9 = 1/4 | ||
| + | :3番目のコインがいかさまの場合 Pr(''E''<sub>3</sub> | B) = Pr(B | ''E''<sub>3</sub>) Pr(''E''<sub>3</sub>) / Pr(''B'') = 1/12 * 1/3 * 9 = 1/4 | ||
| − | です。つまり、3枚のコインをフリップして 表 裏 裏 と出るのを見たことにより、1枚目のコインがいかさまである確率が 1/3 から 1/2 | + | です。つまり、3枚のコインをフリップして 表 裏 裏 と出るのを見たことにより、1枚目のコインがいかさまである確率が 1/3 から 1/2 に上がりました。2枚目、3枚目がいかさまの確率は 1/4 に減っています。 |
| + | |||
| + | ===モンティ・ホール問題=== | ||
| − | |||
テレビショーでプレイヤーの前に3つの扉があり、1つの扉の後ろには景品、残りの2つはハズレになっています。プレイヤーが1つの扉を選択すると、司会者のモンティは残りの扉のうちハズレの扉を開けてみせます。選ぶ扉を残りの開けられていない扉に変更しても良いと言われたとき、プレイヤーはドアを変更すべきでしょうか? | テレビショーでプレイヤーの前に3つの扉があり、1つの扉の後ろには景品、残りの2つはハズレになっています。プレイヤーが1つの扉を選択すると、司会者のモンティは残りの扉のうちハズレの扉を開けてみせます。選ぶ扉を残りの開けられていない扉に変更しても良いと言われたとき、プレイヤーはドアを変更すべきでしょうか? | ||
| − | + | * 答え1:変更したほうが良い。変更しない場合は景品をあてる確率はどの扉も 1/3 である。変更すると 2/3 の確率で景品をもらえる。 | |
| + | |||
| + | * 答え2:変更しても意味はない。ドアを開けられようがそうでなかろうが、そもそも選択肢は3つあり、どの扉の後ろにも等確率で景品がある。よって変更してもしなくても同じである。 | ||
| + | |||
| + | さて上記のどちらが正しいでしょうか。 | ||
Latest revision as of 12:20, 24 April 2012
| Menu: | 確率の定義 | 平均と分散 | 分布 |
Contents |
[edit] 確率の定義
確率を論じるためには
- 起こりうるすべての事象を含む標本空間 Ω
- 実際に起こりうる事象の集合 F
- 各事象が起こる確率を与える関数 Pr: F → R
が必要です。ここで使う関数のことを一般に確率測度とよびます。確率測度は
- Pr(Ω) = 1
- どの事象 E についても 0 ≤ Pr(E) ≤ 1
- 加算個の独立な事象について
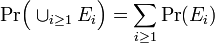
を満たさなくてはならず、コルモゴロフの公理と呼ばれています。Pr(E) を事象 E の確率と呼びます。
[edit] 条件付き確率
事象 F が起こったあとで事象 E が起きる条件付き確率を
Pr( E | F ) = Pr( E ∩ F ) / Pr (F )
と書きます。F が起こる確率の内訳としての Pr( E ∩ F ) を求めるわけです。もし E と F が独立の事象なら Pr( E | F ) = Pr (E ) になります。
[edit] 全確率の法則
任意の確率は、互いに背反な事象 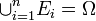 を用いて
を用いて
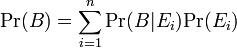
と書けます。
[edit] ベイズの法則
互いに背反な事象 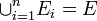 にたいして
にたいして
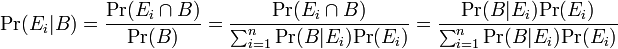
最初と最後のイコールは条件付き確率の定義、次のイコールは全確率の法則です。
事象 Ei に対して Pr( Ei ) は事象 B が起こる前に与えられる確率であるから事前確率といい、Pr( Ei | B ) は B が起こった後で与えられる確率であるから事後確率といいます。
[edit] 例
[edit] いかさまコインを見分ける
3枚のコインがあり、そのうち1枚だけは表が2/3、残りは1/2の確率で出るとします。i 番目のコインがいかさまである事象を Ei と書きましょう。最初に Pr (Ei ) = 1/3 ( i = 1,2,3) とします。
いま、3枚のコインを順に投げて 表 裏 裏 が出たとします。この事象を B と書き、Ei に対する条件付き確率を求めてみます。
- 1番目のコインがいかさまの場合 Pr(B | E1) = 2/3 × 1/2 × 1/2 = 1/6
- 2番目のコインがいかさまの場合 Pr(B | E2) = 1/2 × 1/3 × 1/2 = 1/12
- 2番目のコインがいかさまの場合 Pr(B | E3) = 1/2 × 1/2 × 1/3 = 1/12
- 表裏裏を観測する確率 Pr(B) = Σi3 Pr(B | Ei) Pr(Ei) = 1/6 * 1/3 + 1/12 * 1/3 + 1/12 * 1/3 = 1/9
ここでベイズの法則を用います。表裏裏を観測したあとで、各コインがいかさまである確率を求めてみます。
- 1番目のコインがいかさまの場合 Pr(E1 | B) = Pr(B | E1) Pr(E1) / Pr(B) = 1/6 * 1/3 * 9 = 1/2
- 2番目のコインがいかさまの場合 Pr(E2 | B) = Pr(B | E2) Pr(E2) / Pr(B) = 1/12 * 1/3 * 9 = 1/4
- 3番目のコインがいかさまの場合 Pr(E3 | B) = Pr(B | E3) Pr(E3) / Pr(B) = 1/12 * 1/3 * 9 = 1/4
です。つまり、3枚のコインをフリップして 表 裏 裏 と出るのを見たことにより、1枚目のコインがいかさまである確率が 1/3 から 1/2 に上がりました。2枚目、3枚目がいかさまの確率は 1/4 に減っています。
[edit] モンティ・ホール問題
テレビショーでプレイヤーの前に3つの扉があり、1つの扉の後ろには景品、残りの2つはハズレになっています。プレイヤーが1つの扉を選択すると、司会者のモンティは残りの扉のうちハズレの扉を開けてみせます。選ぶ扉を残りの開けられていない扉に変更しても良いと言われたとき、プレイヤーはドアを変更すべきでしょうか?
- 答え1:変更したほうが良い。変更しない場合は景品をあてる確率はどの扉も 1/3 である。変更すると 2/3 の確率で景品をもらえる。
- 答え2:変更しても意味はない。ドアを開けられようがそうでなかろうが、そもそも選択肢は3つあり、どの扉の後ろにも等確率で景品がある。よって変更してもしなくても同じである。
さて上記のどちらが正しいでしょうか。