Aritalab:Lecture/Basic/Inequality

Latest revision as of 10:10, 8 July 2010

[edit] 分散とモーメント

[定義] E[ $X^k$ ] を確率変数 X の k次モーメントと呼ぶ。

[定義] 確率変数 X の分散は

$\mathbf{Var}[X] = \mathbf{E}[(X-\mathbf{E}[X])^2] = \mathbf{E}[X^2] - (E[X])^2$

[定義]　確率変数 X の標準偏差 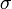$\sigma$ 　は

$\sigma[X] = \sqrt{\mathbf{Var}[X]}$

[edit] Markovの不等式

確率変数 X と a > 0 に対し

$\textstyle \mbox{Pr}(|X| \geq a) \leq \mathbf{E}[|X|]/a$

をマルコフの不等式と呼ぶ。証明は随所に見られるので省略する。

[edit] Chebyshevの不等式

確率変数 X と a > 0 に対し

$\textstyle \mbox{Pr}(|X - \mathbf{E}[X]| \geq a) \leq \mathbf{Var}[X]/a^2$

をチェビシェフの不等式と呼ぶ。証明には、 $\mbox{Pr}(|X - \mathbf{E}[X]| \geq a) = \mbox{Pr}(|X - \mathbf{E}[X]|^2 \geq a^2)$ に対してマルコフの不等式を適用する。

[edit] MarkovとChebyshevの違い

[edit] 変形した一様分布

正の整数 k に対し、確率　1/k で k E[X] をとり、確率 (1- 1/k) で 0　をとる確率変数 X を考えよう。このときマルコフの不等式は $\mbox{Pr}(X \geq k\mathbf{E}[X] ) \leq 1/k$ 　となるが、定義より $\mbox{Pr}(X = k\mathbf{E}[X])=1/k$ なので等号が成立する。つまりマルコフの不等式が十分「きつい」例になっている。

この分布の分散は

$\textstyle \frac{k^2}{k}(\mathbf{E}[X])^2 - (\mathbf{E}[X])^2 = (k-1)(\mathbf{E}[X])^2$

チェビシェフの不等式は

$\textstyle \mbox{Pr}(|X - \mathbf{E}[X]| \geq k\mathbf{E}[X]) \leq (k-1)/k^2$

[edit] 二項分布

裏表が等確率ででるコインを n 回投げて、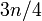 $3n/4$ 回表が出る確率を見積もってみよう。確率変数 X を n 回の試行で表が出る回数とする。コインは公平なので $\mathbf{E}[X] = n/2$ である。分散を考えるにはコイン1枚の試行の分散から考える。

$\mathbf{E}[X_1^2]-(\mathbf{E}[X_1])^2 = 1/2 - (1/2)^2 = 1/4$

確率変数 X の分散は

$\textstyle \mathbf{Var}[X] = \mathbf{Var}\big[ \sum^n X_i \big] = \sum^n \mathbf{Var}[X_i] = n/4$

マルコフの不等式では

$\textstyle \mbox{Pr}(X \geq 3n/4) \leq \frac{\mathbf{E}[X]}{3n/4} = 2/3$

チェビシェフの不等式では

$\textstyle \mbox{Pr}(X \geq 3n/4) = \frac{1}{2} \mbox{Pr}(|X-\mathbf{E}[X]| \geq n/4) \leq \frac{\mathbf{Var}[X]}{(n/4)^2} = 4/n$

@@ Line 24: / Line 24: @@
 ==MarkovとChebyshevの違い==
-===一様分布===
+===変形した一様分布===
-正の整数 ''k'' に対し、確率　1/''k'' で ''k'' '''E'''[''X''] をとり、確率 (1- 1/''k'') で 0　をとる確率変数 ''X'' を考える。 このときマルコフの不等式は <math>\mbox{Pr}(X \geq k\mathbf{E}[X] ) \leq 1/k</math>　となるが、定義より <math>\mbox{Pr}(X = k\mathbf{E}[X])=1/k</math> なので等号が成立する。つまり不等式が十分「きつい」例になっている。
+正の整数 ''k'' に対し、確率　1/''k'' で ''k'' '''E'''[''X''] をとり、確率 (1- 1/''k'') で 0　をとる確率変数 ''X'' を考えよう。 このときマルコフの不等式は <math>\mbox{Pr}(X \geq k\mathbf{E}[X] ) \leq 1/k</math>　となるが、定義より <math>\mbox{Pr}(X = k\mathbf{E}[X])=1/k</math> なので等号が成立する。つまりマルコフの不等式が十分「きつい」例になっている。
-この分布の分散は <math>\textstyle \frac{k^2}{k}(\mathbf{E}[X])^2 - (\mathbf{E}[X])^2 = (k-1)(\mathbf{E}[X])^2</math> となる。チェビシェフの不等式は <math>\textstyle \mbox{Pr}(|X - \mathbf{E}[X]| \geq k\mathbf{E}[X]) \leq (k-1)/k^2</math> を与える。
+この分布の分散は
+:<math>\textstyle \frac{k^2}{k}(\mathbf{E}[X])^2 - (\mathbf{E}[X])^2 = (k-1)(\mathbf{E}[X])^2</math>
+チェビシェフの不等式は
+:<math>\textstyle \mbox{Pr}(|X - \mathbf{E}[X]| \geq k\mathbf{E}[X]) \leq (k-1)/k^2</math>
+===二項分布===
+裏表が等確率ででるコインを ''n'' 回投げて、<math>3n/4</math> 回表が出る確率を見積もってみよう。
+確率変数 ''X'' を ''n'' 回の試行で表が出る回数とする。 コインは公平なので<math>\mathbf{E}[X] = n/2</math>である。分散を考えるにはコイン1枚の試行の分散から考える。
+:<math>\mathbf{E}[X_1^2]-(\mathbf{E}[X_1])^2 = 1/2 - (1/2)^2 = 1/4</math>
+確率変数 ''X'' の分散は
+:<math>\textstyle \mathbf{Var}[X] = \mathbf{Var}\big[ \sum^n X_i \big] = \sum^n \mathbf{Var}[X_i] = n/4</math>
+マルコフの不等式では
+:<math>\textstyle \mbox{Pr}(X \geq 3n/4) \leq \frac{\mathbf{E}[X]}{3n/4} = 2/3</math>
+チェビシェフの不等式では
+:<math>\textstyle \mbox{Pr}(X \geq 3n/4) = \frac{1}{2} \mbox{Pr}(|X-\mathbf{E}[X]| \geq n/4) \leq \frac{\mathbf{Var}[X]}{(n/4)^2} = 4/n</math>

Aritalab:Lecture/Basic/Inequality

Latest revision as of 10:10, 8 July 2010

Contents

[edit] 分散とモーメント

[edit] Markovの不等式

[edit] Chebyshevの不等式

[edit] MarkovとChebyshevの違い

[edit] 変形した一様分布

[edit] 二項分布

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

metabolites

Toolbox