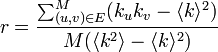Aritalab:Lecture/NetworkBiology/Degree Distribution
From Metabolomics.JP
次数分布
次数 k が全頂点の中で占める割合 p(k) を次数分布といいます。
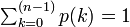
その平均値を、平均次数といい <k> = Σ k p(k) と書きます。
隣接点の次数分布
隣接する頂点の次数を 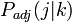 と書きましょう。ここで次数 k と隣接する頂点の次数 j が独立に決まるとします(相関が0)。
すると次の式から、次数が j の頂点は相対的に j / <k> だけ、隣にきやすいはずです。
と書きましょう。ここで次数 k と隣接する頂点の次数 j が独立に決まるとします(相関が0)。
すると次の式から、次数が j の頂点は相対的に j / <k> だけ、隣にきやすいはずです。
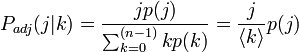
隣の頂点には、ハブが来やすいことがわかります。その来やすさは、頂点の次数に正比例します。
次数相関
隣接する頂点どうしの次数が似る度合いを次数相関といいます。 辺がランダムに張られる場合は次数相関は 0 になりますが、映画俳優の競演関係といったネットワークはハブどうしが隣接する、つまり正の相関を持つ (assortative) ことが知られています。 生態系のような生物学ネットワークでは負の相関を持つ (disassortative) と考えられます。
次数相関の存在は次数 k の頂点につながる隣接点の平均次数を調べるとわかります。隣接点の平均次数は、次数分布や頂点の次数 k によらず一定値となります。
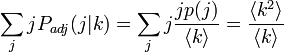
次数相関 r をピアソンの相関係数に従って定義しましょう。M 本ある辺の両端点 u, v の次数をそれぞれ ku, ku とおきます。相関係数の分子は ku, kv の平均からの差分を計算します。
分母は ku と kv の標準偏差の積ですが、実際には分散を計算します。