Aritalab:Lecture/Basic/Inequality

分散とモーメント

[定義] E[$X^k$] を確率変数 X の k　次モーメントと呼ぶ。

[定義] 確率変数 X の分散は

$\mathbf{Var}[X] = \mathbf{E}[(X-\mathbf{E}[X])^2] = \mathbf{E}[X^2] - (E[X])^2$

[定義]　確率変数 X の標準偏差 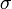$\sigma$　は

をマルコフの不等式と呼ぶ。証明は随所に見られるので省略する。

具体例

• 確率　1/k で k E[X] をとり、確率 (1- 1/k) で 0　をとる確率変数を考える。 このときマルコフの不等式は $\textstyle \mbox{Pr}(X \geq k\mathbf{E}[X] ) = 1/k$　という等号が成立しており、不等式が十分「きつい」ものであることがわかる。

Chebyshevの不等式

確率変数 X と a > 0 に対し

$\textstyle \mbox{Pr}(|X - \mathbf{E}[X]| \geq a) \leq \mathbf{Var}[X]/a^2$

をチェビシェフの不等式と呼ぶ。証明には、$\mbox{Pr}(|X - \mathbf{E}[X]| \geq a) = \mbox{Pr}(|X - \mathbf{E}[X]|^2 \geq a^2)$ に対してマルコフの不等式を適用する。

具体例

• マルコフの不等式において等号を成り立たせた確率分布を考える。チェビシェフの不等式では $\textstyle \mbox{Pr}(|X - \mathbf{E}[X]| \geq a) =$