Aritalab:Lecture/NetworkBiology/Random Walk
m |
m |
||
| Line 1: | Line 1: | ||
{{Lecture/Header}} | {{Lecture/Header}} | ||
| + | |||
| + | ==ランダムウォーク== | ||
| + | ===一次元=== | ||
| + | 原点から出発して1ステップ毎に確率 ''p'' で +1, 1-''p'' で -1 動くランダムウォークを考えましょう。 | ||
| + | ''n'' ステップ後に、正の方向に ''k'' 回進んでいる確率は | ||
| + | <center> <sub>n</sub><big>C</big><sub>k</sub> ''p<sup>k</sup>'' ( 1- ''p'' )<sup>n-k</sup> </center> | ||
| + | であらわされ、二項分布 (英語でbinomial distributionといいます) B(''n'', ''p'' ) に従います。位置の期待値は ''np'' <ref>期待値の定義に従って計算します。 | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | E[X] &= \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=1}^n k \binom{n}{k} p^k(1-p)^{n-k}\\ | ||
| + | &= \sum_{k=1}^n k \frac{n}{k} \binom{n-1}{k-1} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n}{k} \cdot p \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k}\\ | ||
| + | &= np \sum^{n}_{k=1} \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k} = np | ||
| + | \end{align} | ||
| + | </math> | ||
| + | </ref>, 分散は ''np'' (1 - ''p'') <ref>分散の定義に従って計算します。まず | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | E[X^2] &= k^2 \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=0}^n {k(k-1)+k} \binom{n}{k} p^k(1-p)^{n-k}\\ | ||
| + | &= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k}\\ | ||
| + | &= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + np \\ | ||
| + | &= n(n-1) \sum_{k=2}^n k(k-1) \binom{n-2}{k-2} p^{k-2}(1-p)^{n-k} + np \\ | ||
| + | &= n(n-1) p^2 + np | ||
| + | \end{align}</math> | ||
| + | <br/>したがって<br/> | ||
| + | <math>\begin{align} | ||
| + | V[X] &= E[X^2] - (E[X])^2 = n(n-1) p^2 + np - n^2p^2\\ | ||
| + | &= np (1-p) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | </ref>です。 | ||
== グラフ上のランダムウォーク == | == グラフ上のランダムウォーク == | ||
| Line 36: | Line 68: | ||
このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) と呼ぶ。 | このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) と呼ぶ。 | ||
| + | |||
| + | |||
| + | <references/> | ||
Revision as of 06:23, 19 May 2011
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
ランダムウォーク
一次元
原点から出発して1ステップ毎に確率 p で +1, 1-p で -1 動くランダムウォークを考えましょう。 n ステップ後に、正の方向に k 回進んでいる確率は
であらわされ、二項分布 (英語でbinomial distributionといいます) B(n, p ) に従います。位置の期待値は np [1], 分散は np (1 - p) [2]です。
グラフ上のランダムウォーク
グラフ G(V,E) の各頂点 u から出る辺を等確率 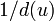 で選んで動くグラフ上のランダムウォークを考えよう。
非周期性を仮定したいので、以下では二部グラフでない連結なものだけを考慮する。
で選んで動くグラフ上のランダムウォークを考えよう。
非周期性を仮定したいので、以下では二部グラフでない連結なものだけを考慮する。
[定理] 頂点 u から v に到達するステップ数の期待値を 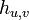 と記述すると
と記述すると 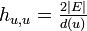 が成立。
が成立。
- 証明
まずランダムウォークの定常分布 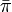 が
が 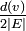 であることを示そう。
定常分布における各頂点上の確率
であることを示そう。
定常分布における各頂点上の確率 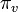 の総和をとると
の総和をとると 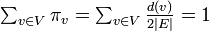 。
。
また
Failed to parse (lexing error): \textstyle \bar \pi {\mathbf P} = \sum_{u \in adj(v)} \pi_u \frac{1}{d(u)} = \sum_{u \in adj(v)} \frac{1}{2 |E|} = \frac{d(v)}{2|E|} = \bar \pi
から、
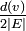 は定常分布の条件を満たす。
は定常分布の条件を満たす。
頂点への再帰時間の期待値は 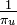 であることを使うと証明は終わり。
であることを使うと証明は終わり。
- 補題
隣り合う頂点間のステップ数の期待値の上限は 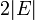 で抑えられる。なぜなら
で抑えられる。なぜなら
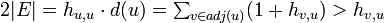
さらにグラフ全体を訪れるのに必要な期待値の上限は 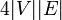 で抑えられる。与えられたグラフのスパニング木を作ると、その上を全点辿ったときの辺数が
で抑えられる。与えられたグラフのスパニング木を作ると、その上を全点辿ったときの辺数が 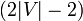 のため
のため
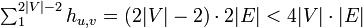
このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) と呼ぶ。
![\begin{align}
E[X] &= \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=1}^n k \binom{n}{k} p^k(1-p)^{n-k}\\
&= \sum_{k=1}^n k \frac{n}{k} \binom{n-1}{k-1} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n}{k} \cdot p \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k}\\
&= np \sum^{n}_{k=1} \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k} = np
\end{align}](/mediawiki/images/math/3/e/6/3e62873053db052b373dd8858582045f.png)
![\begin{align}
E[X^2] &= k^2 \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=0}^n {k(k-1)+k} \binom{n}{k} p^k(1-p)^{n-k}\\
&= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k}\\
&= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + np \\
&= n(n-1) \sum_{k=2}^n k(k-1) \binom{n-2}{k-2} p^{k-2}(1-p)^{n-k} + np \\
&= n(n-1) p^2 + np
\end{align}](/mediawiki/images/math/c/e/a/cea507a5fa466b803f158dbe0908b7f0.png)
![\begin{align}
V[X] &= E[X^2] - (E[X])^2 = n(n-1) p^2 + np - n^2p^2\\
&= np (1-p)
\end{align}](/mediawiki/images/math/4/3/9/439bd925821dc9370834e8ffa8e38e42.png)