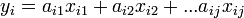|
|
| (2 intermediate revisions by one user not shown) |
| Line 1: |
Line 1: |
| | =確率= | | =確率= |
| − | ===期待値・平均===
| |
| − | 期待値とは、確率変数(サイコロ)の取る値とその確率とをかけた総和です。
| |
| − | 通常「平均」というと、全ての要素が等確率で生じているという前提があるので、数学では期待値という言葉を使います。期待値は E[確率変数] と書きます。
| |
| | | | |
| − | ;例
| + | * [[Aritalab:Lecture/Basic/Expectation|期待値と分散について]] |
| − | : E[フェアなサイコロ] = 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3.5 | + | |
| − | : E[フェアなコインで表が出る] = 1 * 1/2 + 0 * 1/2 = 0.5
| + | |
| | | | |
| − | ;二つの確率変数X,Yがあったとき、和の期待値は、期待値の和に等しい。
| |
| − | ; ''E[X+Y]=E[X]+E[Y]''
| |
| − | 確率変数という言葉をサイコロと考えましょう。二つのサイコロの目を足した数の期待値(平均)は、個々のサイコロの期待値(平均)の和ということです。例えば、サイコロ2個を振って出る目を足した数の平均値を数え上げて求めるのは大変です。目の組み合わせが1,1の場合から6,6の場合まで数え上げなくてはなりません。
| |
| − | しかし、上の式を用いれば簡単に求められます。
| |
| − |
| |
| − | ;例
| |
| − | : E[サイコロ2個] = E[サイコロ1個] + E[サイコロ1個] = 3.5 + 3.5 = 7
| |
| − | : E[コイン10枚で表が出る] = 10 * E[コイン一枚] = 10 * 1/2 = 5
| |
| − |
| |
| − | では、サイコロの目を足すかわりに掛けた場合、目の期待値を簡単に求められるでしょうか。
| |
| − | 二つのサイコロが''独立''のときに限り、期待値は積についても分配できる。
| |
| − |
| |
| − | ;例
| |
| − | :E[サイコロ2個の積] = E[サイコロ1個] * E[サイコロ1個] = 3.5 * 3.5 =
| |
| − |
| |
| − | ===分散===
| |
| − | 分散とは確率変数がとる値のばらつきの度合いである。
| |
| − | :<math>V[X] = E[(X-E[X])^2] = E[X^2] - (E[X])^2</math>
| |
| − | X,Yが独立のときに限り、和の分散は分散の和に等しい。
| |
| − | :<math>V[X+Y] = V[X] + V[Y]</math>(ただしX,Yは独立)
| |
| − | 独立でない場合に生じる「ズレ」を共分散と呼ぶ。
| |
| − | :<math>V[X+Y] = V[X] + V[Y] + 2Cov[X,Y]</math>
| |
| − | ===共分散・相関===
| |
| − | 共分散は二組の対応する確率変数の間で、ばらつきが異なる度合いである。
| |
| − | 共分散の定義は
| |
| − | :<math>Cov[X,Y]=E[ (X-E[X]) (Y-E[Y]) ]</math>
| |
| − | となる。
| |
| − | XとYに関して対称に定義されていて、XとYのばらつきの傾向が似ていれば大きな正の値になり、似ていなければ大きな負の値になる。XとYが独立であれば0になる。
| |
| − | 共分散をXの標準偏差とYの標準偏差で割ったものが相関係数である。
| |
| − | :<math>Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})</math>
| |
| − |
| |
| − | ===ベイズ推定===
| |
| − | ベイズの定理は以下のように表される。
| |
| − | :<math>P(A|B) = P(B|A)P(A)/P(B)</math>
| |
| − | ここでP(A)を事前確率、P(A|B)を(Bが起きることを知った上でのAが起きる確率という意味の)事後確率と呼ぶ。
| |
| − |
| |
| − | <!---
| |
| − | 参考 [http://ja.wikipedia.org/wiki/%E3%83%A2%E3%83%B3%E3%83%86%E3%82%A3%E3%83%BB%E3%83%9B%E3%83%BC%E3%83%AB%E5%95%8F%E9%A1%8C モンティ・ホール問題]
| |
| − | :3つの扉のうち1つだけに賞品が入っている。ただし扉は次のように2段階で選べる。
| |
| − | まず回答者は3つの扉からどれか1つを選ぶ。
| |
| − | 次に、答を知っている司会者が、選んでいない扉で賞品の入っていない扉1つを開けてみせる。ただし、回答者が当たりの扉を選んでいる場合は、残りの扉からランダムに1つを選んで開けるとする。このあと回答者は扉を1回選び直してもよい。
| |
| − | 2で扉を換えるのと換えないのと、どちらが当る確率が高いか?
| |
| − | --->
| |
| | =分布= | | =分布= |
| − | ==正規分布==
| + | * [[Aritalab:Lecture/Basic/Distribution|分布について]] |
| − | よく見る釣鐘型の分布。どんな分布でも、その中から要素をランダムに抽出して和をとったものの分布は、正規分布に近づく(中心極限定理)。期待値が0, 分散が1になるようにスケーリングしたものを標準正規分布といい、<math>N(0,1)</math>と書く。
| + | |
| − | | + | |
| − | ===正規分布表===
| + | |
| − | 標準正規分布表の見方。
| + | |
| − | {|
| + | |
| − | |
| + | |
| − | {| class="wikitable"
| + | |
| − | | z || 0.0 || 0.2 || 0.4 || 0.6 || 0.8
| + | |
| − | |-
| + | |
| − | | 0.0 || 0.5000 || 0.4207 || 0.3446 || 0.2743 || 0.2119
| + | |
| − | |-
| + | |
| − | | 1.0 || 0.1587 || 0.1151 || 0.0808 ||0.0548 || 0.0359
| + | |
| − | |-
| + | |
| − | | 2.0 || 0.0228 || 0.0139 || 0.0082 || 0.0047 || 0.0026
| + | |
| − | |-
| + | |
| − | | 3.0 || 0.0013 || 0.0007 || 0.0003 || 0.0002 || 0.0001
| + | |
| − | |}
| + | |
| − | | [[Image:JSBi-Std.png|200px]]
| + | |
| − | |}
| + | |
| − | 表におけるzの値は上から順に左→右方向にみる。正規分布全体の面積を1.0としたときの、
| + | |
| − | zから上側の面積を示している。例えば標準偏差が2.0以上の面積は0.0228、2.2以上の面積は0.0139。
| + | |
| − | | + | |
| − | ==ポアソン分布==
| + | |
| − | 稀にしか起こらない離散的な事象を数える際に用いる分布。
| + | |
| − | 単位時間中に平均λ回発生する事象が、ぴったりk回発生する確率を
| + | |
| − | {|
| + | |
| − | |
| + | |
| − | :<math>P(N=k) = \frac{e^{-\lambda}\lambda^k}{k!}</math>
| + | |
| − | | [[Image:JSBi-Poisson.png|200px]] | + | |
| − | |}
| + | |
| − | と定義する。
| + | |
| − | | + | |
| − | ==二項分布==
| + | |
| − | コイン投げをして表裏がでる回数を記録したときにできる分布。
| + | |
| − | 離散的な分布だが、フェアなコインを30回程度投げると正規分布で非常によく近似できる。
| + | |
| | | | |
| | =統計・推定= | | =統計・推定= |
従属変数(近似したい値、目的変数ともいう)と説明変数(近似に用いるデータ)の関係を統計的に推定することを回帰分析という。
1個の説明変数から1個の従属変数を予測する場合を単回帰、説明変数を複数用いる場合を重回帰という。
従属変数をy、説明変数をxとすると