Aritalab:Lecture/NetworkBiology/Random Walk
m (→拡散係数) |
(→再帰確率) |
||
| (27 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Lecture/Header}} | {{Lecture/Header}} | ||
| − | == | + | ==1次元ランダムウォーク== |
原点から出発して1ステップ毎に確率 ''p'' で + 1, ''q'' (= 1 − ''p'') で − 1 動くランダムウォークを考えましょう。 | 原点から出発して1ステップ毎に確率 ''p'' で + 1, ''q'' (= 1 − ''p'') で − 1 動くランダムウォークを考えましょう。 | ||
''n'' ステップ後に、正の方向に ''k'' 回進んでいる確率は | ''n'' ステップ後に、正の方向に ''k'' 回進んでいる確率は | ||
| − | < | + | |
| − | であらわされ、二項分布 (binomial distribution) B( ''n'', ''p'' ) に従います。二項分布で正の方向に進むステップ数 ''k'' の期待値は ''np'' <ref>期待値の定義に従って計算します。 | + | <math>\textstyle\binom{n}{k} p^k q^{(n-k)}\ </math> |
| + | |||
| + | であらわされ、二項分布 (binomial distribution) B( ''n'', ''p'' ) に従います。二項分布で正の方向に進むステップ数 ''k'' の期待値は ''np'' <ref>期待値の定義に従って計算します。<br/> | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | E[X] &= \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=1}^n k \binom{n}{k} p^k(1-p)^{n-k}\\ | + | E[X] &= \textstyle\sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=1}^n k \binom{n}{k} p^k(1-p)^{n-k}\\ |
| − | &= \sum_{k=1}^n k \frac{n}{k} \binom{n-1}{k-1} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n}{k} \cdot p \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k}\\ | + | &= \textstyle\sum_{k=1}^n k \frac{n}{k} \binom{n-1}{k-1} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n}{k} \cdot p \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k}\\ |
| − | &= np \sum^{n}_{k=1} \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k} = np | + | &= \textstyle np \sum^{n}_{k=1} \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k} = np |
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | </ref> | + | </ref>なので、''n'' ステップ後の位置の期待値は |
| − | < | + | |
| − | E[ | + | <math>E[k - (n -k)] = E[2k - n] = 2 np - n = n(p - q) \ </math> |
| − | </ | + | |
になります。 | になります。 | ||
| − | 二項分布の分散は ''npq'' <ref>分散の定義に従って計算します。まず | + | 二項分布の分散は ''npq'' です<ref>分散の定義に従って計算します。まず<br/> |
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | E[X^2] &= k^2 \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=0}^n {k(k-1)+k} \binom{n}{k} p^k(1-p)^{n-k}\\ | + | E[X^2] &=\textstyle k^2 \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=0}^n {k(k-1)+k} \binom{n}{k} p^k(1-p)^{n-k}\\ |
| − | &= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k}\\ | + | &=\textstyle \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k}\\ |
| − | &= \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + np \\ | + | &=\textstyle \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + np \\ |
| − | &= n(n-1) \sum_{k=2}^n k(k-1) \binom{n-2}{k-2} p^{k-2}(1-p)^{n-k} + np \\ | + | &=\textstyle n(n-1) \sum_{k=2}^n k(k-1) \binom{n-2}{k-2} p^{k-2}(1-p)^{n-k} + np \\ |
&= n(n-1) p^2 + np | &= n(n-1) p^2 + np | ||
\end{align}</math> | \end{align}</math> | ||
| Line 35: | Line 37: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | </ref> | + | </ref>。原点からの移動距離の 2 乗の期待値は |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | === | + | <math> |
| + | \begin{align} | ||
| + | E[(2 k - n)^2] &= E[4k^2 - 4kn + n^2] = 4 n^2p^2 + 4pqn - 4 n^2p + n^2\\ | ||
| + | &= n^2 + 4 pqn (1-n) = 4pqn + (p-q)^2n^2 | ||
| + | \end{align} | ||
| + | </math> | ||
| − | + | です。 ''p'' = ''q'' = 1/2 の場合は左右に同じ確率で広がり、位置の期待値は 0 です。そのとき移動距離の期待値は ''n''<sup>1/2</sup> です。 | |
| − | + | ||
| − | + | ||
| − | ; | + | ;まとめ |
| − | + | * 位置の期待値 <math> (p-q)n \ </math> | |
| − | + | * 移動距離の期待値 <math>\textstyle \sqrt{(p-q)^2n^2 + 4pqn} </math> | |
| − | * | + | |
| − | + | ||
| − | * | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | === | + | ===再帰確率=== |
| − | + | ||
| − | + | ||
| − | <math>\textstyle \ | + | 原点から出発したランダムウォークが原点に戻ってくる確率を再帰確率といいます。一次元ランダムウォークの場合 |
| + | * 再帰確率 <math>\, r = 1 - | p - q | </math> | ||
| + | * 再帰確率が ''r'' < 1 のときに原点に戻ってくる回数の期待値 <math>\textstyle \frac{r}{1-r} = \frac{1}{|2p - 1|} - 1</math> | ||
| + | となります。<ref> | ||
| + | 再帰確率を c とおきます。一度戻ったらそこからランダムウォークをまた始めるとすれば | ||
| − | + | * ランダムウォークが2回以上ゼロ地点に戻る確率 c<sup>2</sup> | |
| + | * ランダムウォークが3回以上ゼロ地点に戻る確率 c<sup>3</sup> | ||
| + | . | ||
| − | + | となります。だから | |
| − | + | * 戻ってこない確率 = 1 − c | |
| − | </ | + | * ちょうど1回戻る確率 = c − c<sup>2</sup> = c(1 − c) |
| + | * ちょうど2回戻る確率 = c<sup>2</sup> − c<sup>3</sup> = c<sup>2</sup> (1 − c) | ||
| + | . | ||
| + | * ちょうど n 回戻る確率 = c<sup>n</sup> − c<sup>n+1</sup> = c<sup>n</sup> (1 − c) | ||
| − | + | です。戻ってくる回数の期待値は Σ n · c<sup>n</sup> (1 − c) = c / (1 - c) です。 | |
| − | + | </ref> | |
| + | {{GenerateIndex|Aritalab|Lecture/NetworkBiology/Random_Walk/Recurrence|3}} | ||
| − | ; | + | ===[[Aritalab:Lecture/NetworkBiology/Random_Walk/Reflection|反射壁と吸収壁]]=== |
| − | : | + | 反射壁や吸収壁を ''k<sup>*</sup>'' と書くと |
| + | * 反射壁があるとき、''n'' ステップ後に位置 ''k'' に至る経路数は <math> P(k, n; k^*) = P(k, n) + P(2k^* - k, n) \,</math> | ||
| + | * 吸収壁があるとき、''n'' ステップ後に位置 ''k'' に至る経路数は <math> P(k, n; k^*) = P(k, n) - P(2k^* - k, n) \,</math> | ||
| + | となります。([[Aritalab:Lecture/NetworkBiology/Random_Walk/Reflection|詳細]]) | ||
| + | ==2次元ランダムウォーク== | ||
| + | 2 次元の場合は上下左右の 4 方向に移動できます。2n ステップ後に原点に戻っている場合、左右と上下にそれぞれ k, n − k ステップずつ進むと仮定できます。 | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | p^{(2n)}_{00} &= \textstyle\sum^n_{k=0} \frac{(2n)!}{k! k! (n-k)! (n-k)!} \big( \frac{1}{4} \big)^{2n} \\ | ||
| + | &=\textstyle\frac{(2n)!}{(n!)^2} \sum^n_{k=0} \big( \frac{n!}{k!(n-k)!} \big)^2 \big( \frac{1}{4} \big)^{2n} \\ | ||
| + | &=\textstyle\frac{(2n)!}{(n!)^2} \sum^n_{k=0} \binom{n}{k}^2 \big( \frac{1}{4} \big)^{2n} | ||
| + | \end{align} | ||
| + | </math> | ||
| − | + | ここでヴァンデルモンドの畳み込みから <math>\textstyle\sum^n_{k=0}\binom{n}{k}^2 = \binom{2n}{n}</math> なので | |
| − | + | ||
| − | + | <math> | |
| + | p^{(2n)}_{00} = \textstyle \frac{(2n)!}{(n!)^2}\binom{2n}{n}\big(\frac{1}{4}\big)^{2n} = \big[ \frac{(2n)!}{(n!)^2} \big]^2 \frac{1}{4^{2n}} | ||
| + | </math> | ||
| − | <math>\ | + | さらにスターリングの公式 <math>n! \sim n^n e^{-n} \sqrt{2\pi n}</math> を使うと |
| − | + | <math> | |
| + | p^{(2n)}_{00} \sim \textstyle \big[ \frac{(2n)^{2n} e^{-2n} \sqrt{4 \pi n} }{n^{2n} e^{-2n} 2 \pi n} \big]^2 \frac{1}{4^{2n}} = \big[ \frac{4^n}{\sqrt{\pi n}} \big]^2 \frac{1}{4^{2n}} = \frac{1}{\pi n} | ||
| + | </math> | ||
| − | <math> | + | 原点に戻る回数の総計は発散しますが(再帰確実)、 <math>p^{(2n)}_{00} \xrightarrow{n \rightarrow \infty} 0</math> のため、原点はゼロ再帰性を満たします。全ての点は同値類に属すので、平面全体がゼロ再帰性(定常分布 π<sub>ij</sub> = 0) となります。 |
| − | + | ==3次元ランダムウォーク== | |
| − | + | 3 次元の場合、上下、左右、前後にそれぞれ k, j, (n − k − j) 回ずつ移動して 2n ステップ後に原点に戻ると仮定できます。 | |
| − | + | <math> | |
| + | \begin{align} | ||
| + | p^{(2n)}_{000} &= \textstyle\sum_{(j+k)\leq n} \frac{(2n)!}{(k!)^2 (j!)^2 [(n-k-j)!]^2} \big( \frac{1}{6} \big)^{2n} \\ | ||
| + | &=\textstyle\frac{(2n)!}{(n!)^2 2^{2n}} \sum_{(j+k)\leq n} \big( \frac{n!}{k!j!(n-k-j)!} \big)^2 \big( \frac{1}{3} \big)^{2n} \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | この式を閉じた形にするのは大変なので上限値を見積もりましょう。 | ||
| + | |||
| + | 一般に 3 項分布から以下が成立します。 | ||
| + | |||
| + | <math> | ||
| + | \textstyle\sum_{(j+k)\leq n}\frac{n!}{k!j!(n-k-j)!} \frac{1}{3^n} = 1, \quad | ||
| + | \textstyle\frac{n!}{k!j!(n-k-j)!} \leq \frac{n!}{[(n/3)!]^3} | ||
| + | </math> | ||
| + | |||
| + | これより大雑把な見積もりですが | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | p^{(2n)}_{000} &\leq \textstyle\frac{(2n)!}{2^{2n}(n!)^2} \frac{n!}{[(n/3)!]^3} \frac{1}{3^n}\\ | ||
| + | &\sim \textstyle\frac{1}{2^{2n}} \frac{(2n)^{2n} e^{-2n}\sqrt{4\pi n}}{n^n e^{-n} \sqrt{2 \pi n} (n/3)^n e^{-n} (\sqrt{2\pi n/3})^3} \frac{1}{3^n}\\ | ||
| + | &= \textstyle\frac{1}{2}\big(\frac{3}{\pi n}\big)^{3/2} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | 原点に戻る回数の総計が有限となるため <math>\textstyle\sum^{\infty}_{n=0} p^{(2n)}_{000} = \textstyle\sum^{\infty}_{n=0} \frac{c}{n^{3/2}} < \infty \ (c = const.)</math>、空間全体は再帰不確実 (transient) です。 | ||
| + | |||
| + | ここまでのランダムウォークをみると、m 次元ランダムウォークは | ||
| + | |||
| + | <math> | ||
| + | p^{(2n)}_{0^m} \leq c/(\sqrt{\pi n})^{m/2} | ||
| + | </math> | ||
| + | |||
| + | であることが予想されます。3 次元以降はすべて非再帰的になります。 | ||
| + | |||
| + | |||
| + | ==拡散係数== | ||
| + | |||
| + | ランダムウォークを時間の関数として捉えるため、''τ'' 秒毎にステップを刻むことにして歩幅を ''δ'' cm とします。つまり、ステップ数 ''n'' = ''t'' / ''τ'' です。拡散の度合いは分散であらわされます。対称な二項分布の分散は ''n'' = (''t''/''τ'') ''δ''<sup>2</sup> = 2 (''δ''<sup>2</sup> /2 ''τ'') ''t'' となります(分散は距離の 2 乗平均なので ''δ'' が 2 乗されるところに注意)。 | ||
| + | 拡散係数を ''D'' = ''δ''<sup>2</sup> /2 ''τ'' (単位は cm<sup>2</sup>/sec) と書くと、分散は 2 ''Dt'' です。拡散に要する時間は、''t'' = (距離)<sup>2</sup> / 2 ''D'' になります。 | ||
| + | 水中の小分子なら ''D'' ∼ 10<sup>− 5</sup> 、空気中の小分子なら ''D'' ∼ 10<sup>− 1</sup> 程度であることが知られています。 | ||
;考察 | ;考察 | ||
| − | : | + | コーヒークリームがカップの中で広がったり、隣の人が香水をつけているかすぐ分かるのは、分子の拡散が原因ではなく水や空気の対流 |
| + | や攪拌のおかげです。拡散に必要な時間を計算してみましょう。 | ||
| + | * 水中の小分子が拡散のみで ''x'' = 10<sup>-4</sup> cm = 1 μ m (大腸菌のサイズ) 進むのに必要な時間 | ||
| + | :: ''t'' = ''x''<sup>2</sup>/2''D'' = 10<sup>-8</sup>/(2 × 10<sup>-5</sup>) = 5 × 10<sup>-4</sup> 秒 (0.5 ミリ秒) | ||
| + | * 水中の小分子が拡散のみで ''x'' = 10 cm 進むのに必要な時間 | ||
| + | :: ''t'' = ''x''<sup>2</sup>/2''D'' = (10)<sup>2</sup> /(2 × 10<sup>-5</sup>) = 5 × 10<sup>6</sup> 秒 = 2 ヶ月 | ||
| + | * 空気中の小分子が拡散のみで ''x'' = 1 m 進むのに必要な時間 | ||
| + | :: ''t'' = ''x''<sup>2</sup>/2''D'' = (100)<sup>2</sup> / (2 × 10<sup>-1</sup>) = 5 × 10<sup>4</sup> 秒 = 14 時間 | ||
== 有限グラフ上のランダムウォーク == | == 有限グラフ上のランダムウォーク == | ||
| Line 109: | Line 175: | ||
また | また | ||
<math>\textstyle | <math>\textstyle | ||
| − | \bar \pi {\mathbf P} | + | \bar \pi {\mathbf P} |
= \sum_{u \in adj(v)} \pi_u \frac{1}{d(u)} | = \sum_{u \in adj(v)} \pi_u \frac{1}{d(u)} | ||
= \sum_{u \in adj(v)} \frac{1}{2 |E|} = \frac{d(v)}{2|E|} = \bar \pi | = \sum_{u \in adj(v)} \frac{1}{2 |E|} = \frac{d(v)}{2|E|} = \bar \pi | ||
Latest revision as of 15:01, 27 August 2015
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
[edit] 1次元ランダムウォーク
原点から出発して1ステップ毎に確率 p で + 1, q (= 1 − p) で − 1 動くランダムウォークを考えましょう。 n ステップ後に、正の方向に k 回進んでいる確率は
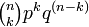
であらわされ、二項分布 (binomial distribution) B( n, p ) に従います。二項分布で正の方向に進むステップ数 k の期待値は np [1]なので、n ステップ後の位置の期待値は
![E[k - (n -k)] = E[2k - n] = 2 np - n = n(p - q) \](/mediawiki/images/math/2/d/e/2de66bc6df6da2d443040b78ba65070d.png)
になります。 二項分布の分散は npq です[2]。原点からの移動距離の 2 乗の期待値は
![\begin{align}
E[(2 k - n)^2] &= E[4k^2 - 4kn + n^2] = 4 n^2p^2 + 4pqn - 4 n^2p + n^2\\
&= n^2 + 4 pqn (1-n) = 4pqn + (p-q)^2n^2
\end{align}](/mediawiki/images/math/8/2/9/829b24cd4ca2ef34bea03014694741da.png)
です。 p = q = 1/2 の場合は左右に同じ確率で広がり、位置の期待値は 0 です。そのとき移動距離の期待値は n1/2 です。
- まとめ
- 位置の期待値
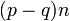
- 移動距離の期待値
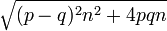
[edit] 再帰確率
原点から出発したランダムウォークが原点に戻ってくる確率を再帰確率といいます。一次元ランダムウォークの場合
- 再帰確率
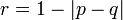
- 再帰確率が r < 1 のときに原点に戻ってくる回数の期待値
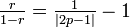
となります。[3]
[edit] 反射壁と吸収壁
反射壁や吸収壁を k* と書くと
- 反射壁があるとき、n ステップ後に位置 k に至る経路数は
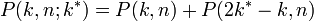
- 吸収壁があるとき、n ステップ後に位置 k に至る経路数は
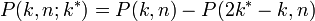
となります。(詳細)
[edit] 2次元ランダムウォーク
2 次元の場合は上下左右の 4 方向に移動できます。2n ステップ後に原点に戻っている場合、左右と上下にそれぞれ k, n − k ステップずつ進むと仮定できます。
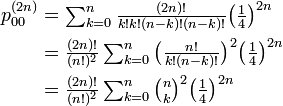
ここでヴァンデルモンドの畳み込みから 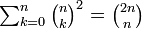 なので
なので
![p^{(2n)}_{00} = \textstyle \frac{(2n)!}{(n!)^2}\binom{2n}{n}\big(\frac{1}{4}\big)^{2n} = \big[ \frac{(2n)!}{(n!)^2} \big]^2 \frac{1}{4^{2n}}](/mediawiki/images/math/5/9/e/59e96ab0879a28767b2079f55f5c6813.png)
さらにスターリングの公式 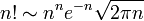 を使うと
を使うと
![p^{(2n)}_{00} \sim \textstyle \big[ \frac{(2n)^{2n} e^{-2n} \sqrt{4 \pi n} }{n^{2n} e^{-2n} 2 \pi n} \big]^2 \frac{1}{4^{2n}} = \big[ \frac{4^n}{\sqrt{\pi n}} \big]^2 \frac{1}{4^{2n}} = \frac{1}{\pi n}](/mediawiki/images/math/7/d/4/7d44b8ee24c8d6be934341331e0524da.png)
原点に戻る回数の総計は発散しますが(再帰確実)、 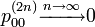 のため、原点はゼロ再帰性を満たします。全ての点は同値類に属すので、平面全体がゼロ再帰性(定常分布 πij = 0) となります。
のため、原点はゼロ再帰性を満たします。全ての点は同値類に属すので、平面全体がゼロ再帰性(定常分布 πij = 0) となります。
[edit] 3次元ランダムウォーク
3 次元の場合、上下、左右、前後にそれぞれ k, j, (n − k − j) 回ずつ移動して 2n ステップ後に原点に戻ると仮定できます。
![\begin{align}
p^{(2n)}_{000} &= \textstyle\sum_{(j+k)\leq n} \frac{(2n)!}{(k!)^2 (j!)^2 [(n-k-j)!]^2} \big( \frac{1}{6} \big)^{2n} \\
&=\textstyle\frac{(2n)!}{(n!)^2 2^{2n}} \sum_{(j+k)\leq n} \big( \frac{n!}{k!j!(n-k-j)!} \big)^2 \big( \frac{1}{3} \big)^{2n} \\
\end{align}](/mediawiki/images/math/b/a/6/ba6c1ac01a3bf5e2425efadcf7ba6f04.png)
この式を閉じた形にするのは大変なので上限値を見積もりましょう。
一般に 3 項分布から以下が成立します。
![\textstyle\sum_{(j+k)\leq n}\frac{n!}{k!j!(n-k-j)!} \frac{1}{3^n} = 1, \quad
\textstyle\frac{n!}{k!j!(n-k-j)!} \leq \frac{n!}{[(n/3)!]^3}](/mediawiki/images/math/7/c/e/7ce2322d1ca03802f857b61149963cb4.png)
これより大雑把な見積もりですが
![\begin{align}
p^{(2n)}_{000} &\leq \textstyle\frac{(2n)!}{2^{2n}(n!)^2} \frac{n!}{[(n/3)!]^3} \frac{1}{3^n}\\
&\sim \textstyle\frac{1}{2^{2n}} \frac{(2n)^{2n} e^{-2n}\sqrt{4\pi n}}{n^n e^{-n} \sqrt{2 \pi n} (n/3)^n e^{-n} (\sqrt{2\pi n/3})^3} \frac{1}{3^n}\\
&= \textstyle\frac{1}{2}\big(\frac{3}{\pi n}\big)^{3/2}
\end{align}](/mediawiki/images/math/b/6/7/b67abf5e39354b42a82522ca5d330fc8.png)
原点に戻る回数の総計が有限となるため 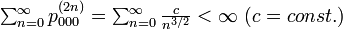 、空間全体は再帰不確実 (transient) です。
、空間全体は再帰不確実 (transient) です。
ここまでのランダムウォークをみると、m 次元ランダムウォークは
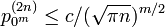
であることが予想されます。3 次元以降はすべて非再帰的になります。
[edit] 拡散係数
ランダムウォークを時間の関数として捉えるため、τ 秒毎にステップを刻むことにして歩幅を δ cm とします。つまり、ステップ数 n = t / τ です。拡散の度合いは分散であらわされます。対称な二項分布の分散は n = (t/τ) δ2 = 2 (δ2 /2 τ) t となります(分散は距離の 2 乗平均なので δ が 2 乗されるところに注意)。 拡散係数を D = δ2 /2 τ (単位は cm2/sec) と書くと、分散は 2 Dt です。拡散に要する時間は、t = (距離)2 / 2 D になります。 水中の小分子なら D ∼ 10− 5 、空気中の小分子なら D ∼ 10− 1 程度であることが知られています。
- 考察
コーヒークリームがカップの中で広がったり、隣の人が香水をつけているかすぐ分かるのは、分子の拡散が原因ではなく水や空気の対流 や攪拌のおかげです。拡散に必要な時間を計算してみましょう。
- 水中の小分子が拡散のみで x = 10-4 cm = 1 μ m (大腸菌のサイズ) 進むのに必要な時間
- t = x2/2D = 10-8/(2 × 10-5) = 5 × 10-4 秒 (0.5 ミリ秒)
- 水中の小分子が拡散のみで x = 10 cm 進むのに必要な時間
- t = x2/2D = (10)2 /(2 × 10-5) = 5 × 106 秒 = 2 ヶ月
- 空気中の小分子が拡散のみで x = 1 m 進むのに必要な時間
- t = x2/2D = (100)2 / (2 × 10-1) = 5 × 104 秒 = 14 時間
[edit] 有限グラフ上のランダムウォーク
グラフ G( V , E ) の各頂点 u から出る辺を等確率 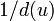 で選んで動くグラフ上のランダムウォークを考えましょう。非周期性を仮定したいので、ここでは二部グラフでない連結なものだけを考慮します。すると、グラフの全頂点をまわるのに必要なランダムウォークの平均ステップ数は 4|V| · |E| 以下であることを示せます。
で選んで動くグラフ上のランダムウォークを考えましょう。非周期性を仮定したいので、ここでは二部グラフでない連結なものだけを考慮します。すると、グラフの全頂点をまわるのに必要なランダムウォークの平均ステップ数は 4|V| · |E| 以下であることを示せます。
[定理] 頂点 u から v に到達するステップ数の期待値を 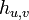 と記述すると
と記述すると 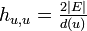 が成立する。
が成立する。
- 証明
まずランダムウォークの定常分布 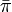 が 各頂点 v において
が 各頂点 v において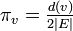 であると仮定してみましょう。
各頂点上の確率
であると仮定してみましょう。
各頂点上の確率 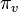 の総和をとると
の総和をとると 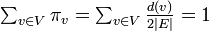 。
。
また
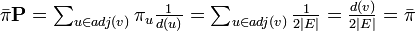 から、
から、
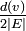 は定常分布の条件を満たしています。
は定常分布の条件を満たしています。
各頂点への再帰時間の期待値は 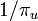 になるので、証明は終わりです。
になるので、証明は終わりです。
[補題] 隣り合う頂点間のステップ数の期待値の上限は 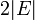 で抑えられる。
で抑えられる。
- 証明
各頂点への再帰時間の期待値を、二通りに計算してみます。
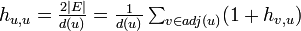
つまり 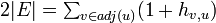 ですから
ですから 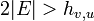 です。
です。
[補題] グラフ全体を訪れるのに必要な期待値の上限は 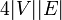 で抑えられる。
で抑えられる。
- 証明
与えられたグラフ全体をスパンする木を作ります。その上を全点辿ったときの辺数は 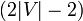 です。
です。
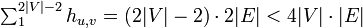
このように、ある頂点から出発したランダムウォークが全ての頂点を訪れるまでの期待ステップ数をグラフの被覆時間 (cover time) と呼びます。
[edit] 参考:式の導出
本文中に出てくる式の導出です。
- ↑ 期待値の定義に従って計算します。
![\begin{align}
E[X] &= \textstyle\sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=1}^n k \binom{n}{k} p^k(1-p)^{n-k}\\
&= \textstyle\sum_{k=1}^n k \frac{n}{k} \binom{n-1}{k-1} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n}{k} \cdot p \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k}\\
&= \textstyle np \sum^{n}_{k=1} \binom{n-1}{k-1} p^{k-1}(1-p)^{n-k} = np
\end{align}](/mediawiki/images/math/6/2/e/62efa38b3d85f5b2231f1a30429cd148.png)
- ↑ 分散の定義に従って計算します。まず
![\begin{align}
E[X^2] &=\textstyle k^2 \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k} = \sum_{k=0}^n {k(k-1)+k} \binom{n}{k} p^k(1-p)^{n-k}\\
&=\textstyle \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + \sum_{k=0}^n k \binom{n}{k} p^k(1-p)^{n-k}\\
&=\textstyle \sum_{k=0}^n k(k-1) \binom{n}{k} p^k(1-p)^{n-k} + np \\
&=\textstyle n(n-1) \sum_{k=2}^n k(k-1) \binom{n-2}{k-2} p^{k-2}(1-p)^{n-k} + np \\
&= n(n-1) p^2 + np
\end{align}](/mediawiki/images/math/0/4/1/041a8967f8c2babc61c31e10db23324e.png)
したがって
![\begin{align}
V[X] &= E[X^2] - (E[X])^2 = n(n-1) p^2 + np - n^2p^2\\
&= np (1-p)
\end{align}](/mediawiki/images/math/4/3/9/439bd925821dc9370834e8ffa8e38e42.png)
- ↑
再帰確率を c とおきます。一度戻ったらそこからランダムウォークをまた始めるとすれば
- ランダムウォークが2回以上ゼロ地点に戻る確率 c2
- ランダムウォークが3回以上ゼロ地点に戻る確率 c3
- 戻ってこない確率 = 1 − c
- ちょうど1回戻る確率 = c − c2 = c(1 − c)
- ちょうど2回戻る確率 = c2 − c3 = c2 (1 − c)
- ちょうど n 回戻る確率 = cn − cn+1 = cn (1 − c)