Aritalab:Lecture/Basic/Probability Generating Function
From Metabolomics.JP
< Aritalab:Lecture | Basic(Difference between revisions)
m (→ポアソン分布) |
m |
||
| Line 98: | Line 98: | ||
\mbox{U}_n''(1) + \mbox{U}_n'(1) - \mbox{U}_n'(1)^2 = \frac{n^2-1}{12}. | \mbox{U}_n''(1) + \mbox{U}_n'(1) - \mbox{U}_n'(1)^2 = \frac{n^2-1}{12}. | ||
</math> | </math> | ||
| + | |||
| + | ==連続分布と積率母関数== | ||
| + | |||
| + | 積率母関数の説明を入れる。 | ||
| + | |||
==ポアソン分布== | ==ポアソン分布== | ||
| Line 107: | Line 112: | ||
</math> | </math> | ||
| − | + | 離散型の確率母関数では | |
<math> | <math> | ||
| Line 121: | Line 126: | ||
= \lambda | = \lambda | ||
</math> | </math> | ||
| + | |||
| + | 連続型の積率母関数では | ||
==指数分布== | ==指数分布== | ||
Revision as of 10:17, 14 December 2012
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
まとめ
確率母関数 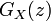 が与えられたとき
が与えられたとき
- 平均
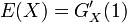
- 分散
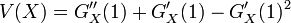
| 分布名 | 分布関数 | 母関数 | 平均 | 分散 |
|---|---|---|---|---|
| 一様分布 |  |
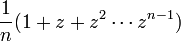 |
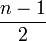 |
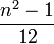
|
| ポアソン分布 | 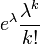 |
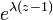 |
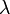 |
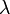
|
| 指数分布 | 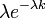 |
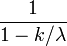 |
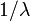 |
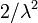
|
確率母関数
ある確率分布 Pr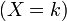 の確率母関数 (probability generating function または pgf) を以下のように定義します。
の確率母関数 (probability generating function または pgf) を以下のように定義します。
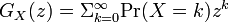
確率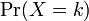 は全て正の値で k について全て足しあわせると 1 になります。
は全て正の値で k について全て足しあわせると 1 になります。
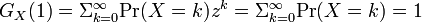
逆に係数が非負で 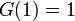 であるようなべき級数
であるようなべき級数 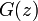 があれば、それは何らかの確率母関数といいます。
があれば、それは何らかの確率母関数といいます。
平均と分散
確率母関数を使うと平均と分散の計算が容易にできます。
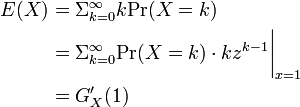
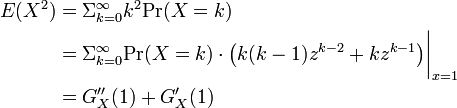
したがって
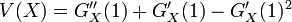
一様分布
n次の一様分布 (uniform distribution) とは確率変数が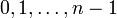 の値を確率
の値を確率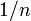 でとるものです。
でとるものです。
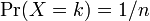
確率母関数は以下の等比級数になります。
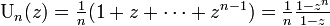
この式は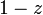 を分母に含んでしまうため、
を分母に含んでしまうため、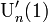 や
や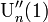 を求める際に不都合です。そこでテイラーの定理を応用します。
を求める際に不都合です。そこでテイラーの定理を応用します。
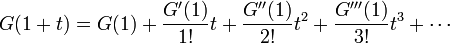
この係数、つまり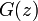 の導関数を以下の式と見比べます。
の導関数を以下の式と見比べます。
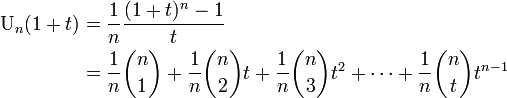
ここから
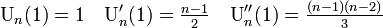
平均と分散は
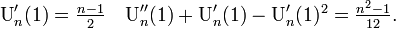
連続分布と積率母関数
積率母関数の説明を入れる。
ポアソン分布
ポアソン分布とは単位時間中に平均  回発生する事象がちょうど k 回発生する確率をあらわしています。
回発生する事象がちょうど k 回発生する確率をあらわしています。
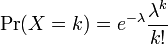
離散型の確率母関数では
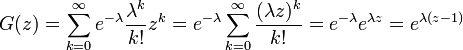
平均と分散は
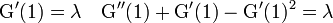
連続型の積率母関数では
指数分布
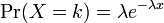
確率母関数は
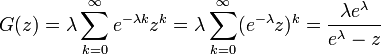
平均と分散は