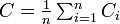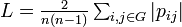Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model
m (→次数の分布) |
m (→クラスター係数) |
||
| Line 13: | Line 13: | ||
==クラスター係数== | ==クラスター係数== | ||
| − | |||
| − | |||
| − | + | クラスター係数は隣接する頂点間の辺の密度の平均値にあたります。まず各頂点 ''i'' におけるクラスター係数 <math>C_i</math> を以下のように定義します。辺の長さはすべて 1 とし <math>(|e| = 1)</math>、頂点 ''i'' の次数を ''deg'' (''i'' ), 隣接する頂点群を ''adj'' (''i'' ) とします。 | |
:<math>\textstyle C_i=\frac{2}{deg(i)(deg(i)-1)} \sum_{j,k \in adj(i)} |e_{jk}|</math> | :<math>\textstyle C_i=\frac{2}{deg(i)(deg(i)-1)} \sum_{j,k \in adj(i)} |e_{jk}|</math> | ||
Revision as of 09:48, 7 December 2012
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
ここでは頂点がすべて連結した無向グラフを扱います。
歴史と参考図書
- Erdős P, Rényi A. "On Random Graphs. I.". Publicationes Mathematicae 6:290–297, 1959
- Erdős P, Rényi A. "The Evolution of Random Graphs". Publ. Math. Inst. Hung. Acad. Sci 5:17–61, 1960
- Bollobás B. Random Graphs (2nd ed.), Cambridge University Press, 2001
- Durrett R. Random Graph Dynamics, Cambridge University Press, 2004
ネットワークの指標: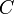
と
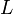
ネットワーク全体についての尺度として、クラスター係数 C と平均頂点間距離 L を紹介します。
クラスター係数
クラスター係数は隣接する頂点間の辺の密度の平均値にあたります。まず各頂点 i におけるクラスター係数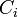 
を以下のように定義します。辺の長さはすべて 1 とし 
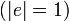、頂点 i の次数を deg (i ), 隣接する頂点群を adj (i ) とします。
グラフ全体のクラスター係数はその平均値です。
クラスター係数が 0.2 や 0.3 になるネットワークは、比較的「密」だといえます。（これから実例をみていきます。）
平均頂点間距離
ここでは頂点 i, j 間の最短経路を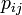 
と書きます。平均頂点間距離の定義はその字のごとく全頂点間の最短路の平均値です。ネットワーク G の頂点数を n とすると頂点の組み合わせの数が n (n - 1) / 2 あるので
となります。
上の定義だと、例えば無限の広がりを持つ数直線の L を求められません (無限個の最短路を計算しなくてはならない)。そういう場合は、ネットワーク上のある点に注目して L を計算できます。その点から距離 L 以内にある頂点数を数えることで L の値を求められます。（これから実例をみていきます。）
様々なグラフにおける C と L
完全グラフ
全ての頂点間に辺を持つグラフを、完全グラフ (complete graph) といいます。完全グラフでは、 C = L = 1 になります。
木
簡単のため全頂点が同じ次数を持つ木を考えましょう。中心の頂点 v0 を根 (root) と呼びます。木はその定義よりサイクルを持たないので C = 0 です。また平均頂点間距離は、距離 L 以内にある頂点を数えることで求められます。
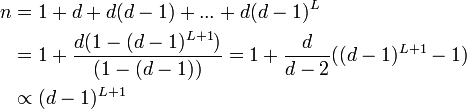
この関係から（大雑把ですが）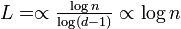 
となります。
格子
格子状のネットワークでは頂点が一定間隔で配置されるため、道路網のような地理的制約をうけるつながりを表現するのに適しています。平面の場合は三角格子、正方格子、六方格子などが考えられます。ただし、クラスター係数を定義のまま適用すると、三角格子以外は隣接頂点どうしがつながらないために常に C = 0 になります。これでは面白くないので、格子の場合は最短距離が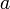 
以下の点には全て辺を張るバリエーションを考えるのが一般的です。
ここでは、d 次元空間において辺の長さが単位距離の格子を Zd と書きましょう。
- Zd において deg( i ) = 2 d
Z1
一次元の格子とは、いわゆる数直線です。ある頂点から k の距離内にある頂点数 n = k + 1 で、これらの頂点への距離の平均値は L = k/2 になります。したがって L ∼ n/2 です。
Z2
二次元の格子として、正方格子を考えます。ある頂点から k の距離内にある頂点数は n = k2 + ( k + 1)2 で与えられ、これらの頂点への距離の平均値が L = k / 2 です。n の式を k について解くと k = {(2 n -1)1/2 - 1} ∼ (2 n)1/2 となるため L ∼ (n / 2) 1/2 です。
Erdős–Rényiグラフ
全ての頂点間に一定の確率 p で独立に辺を作成してできるランダムグラフをErdős–Rényiグラフと呼びます。各頂点に注目してみると n -1 点に対して確率 p で辺を張るため、その次数は二項分布
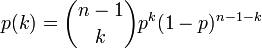
に従います。
次数の分布
各頂点についてみると、n -1 点に対して確率 p で辺を張るため平均次数は ( n -1) p です。
次数分布は二項分布になりますが、このままだと n を大きくすればいくらでも次数の大きな頂点が存在してしまいます。
しかし、現実のネットワークでは次数に上限がある場合がほとんどです。
そのため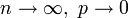 
でかつ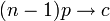 
( c は正の定数) という仮定をします。このとき、二項分布はポアソン分布で近似できます。
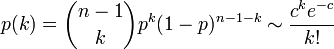
ここで c は次数 k の平均値 (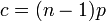
) です。
ポアソン分布は k が大きい場合はべき分布よりもずっと小さな値をとるため、ハブ頂点はできにくくなります。
ネットワークの進化
次数の平均値 c = ( n -1) p を変化させて生じるグラフ形状の違いを検証します。
- c << 1 / n2 のとき
生成される辺数の期待値は pn (n -1) / 2 = cn/ 2 になります。n を無限大にしたとき、この値が 0 に近づくのでネットワークのサイズに対してほとんど辺を持たないことになります。
- c = 1 / n のとき
上と同じ理由で、ネットワーク全体で辺が定数本だけ作られるネットワークになります。ほとんどの辺がばらばらに存在します。
- c = const.
各頂点が一定数の辺を持つことを意味します。 ちょうど c = 1 だと二部グラフのマッチングです。c = 2 だと閉路の集合になります。
各頂点が持つ辺の本数（の期待値）が c なので、c < 1 のときは連結部分の大きさが高々 log n 程度にしかなりません。しかし c > 1 としたとたん、繋がっていく確率のほうが高くなります。その半径 (diameter) を k とおくと ck = n まで成長できるので k = log n / log c です。
詳細な解析によると、臨界点にあたる c = 1 では連結部分のサイズが O (n 2/3) になることが知られています。
- c = log n
全体が連結になります。
ある頂点が辺を全く持たない確率を考えます。 (1 - p)n-1 = { ( 1 - c /(n - 1))(n - 1)/c }c <= e-c。したがって、そのような頂点がグラフ中に存在しない確率の上限は ne-c となります。これを 0 に収束させるには例えば c >= 2 log n で十分です。このとき孤立点が消滅します。
- 相転移
上でみたように、次数の平均値が 1 をこえると急に連結成分のサイズが大きくなり、 log n に達すると全体が連結になります。 こうした点を、相転移点と呼びます。
辺の数を固定したい場合
ERモデルにおいて、辺の数を正確に N 本とする場合を考えます。n 頂点からランダムに2つを選び、その間に辺を作成するプロセスを正確に N 回繰り返します。(ランダムに頂点を選ぶ回数は m = 2 N。)これは次数の期待値が p = 2 N / n(n -1) のERグラフにおいて、たまたま辺数が N となった場合に相当します。
ERモデルの特徴
- クラスター係数
辺が張られる確率は全て独立なので C ( p ) = p ∼ c / n です。これは、完全グラフをほとんど含まないことを意味しています。
- 平均頂点間距離
各頂点が持つ辺の期待値を c = ( n -1) p とします。
- L( p ) >= log n / log c = O(log n )
- 連結性
ERグラフ全体が連結であるためには、次数が O(log n ) 以上必要です。
