Aritalab:Lecture/NetworkBiology/Markov Chains/StationaryDistribution

From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology | Markov Chains(Difference between revisions)
Jump to: navigation, search
m (→‎Abel の収束定理)
m (→‎Abel の収束定理)
 
(4 intermediate revisions by one user not shown)
Line 55: Line 55:
  
 
==Abel の収束定理==
 
==Abel の収束定理==
−
以下の定理 (Abelの定理) は証明せずに利用します。
+
以下の定理 (Abelの定理) は証明せずに利用します。この定理と母関数の関係から、再帰性を <math>\textstyle\sum_n f^{(n)}</math> ではなく <math>\textstyle\sum_n p^{(n)}</math> で議論できるようになり、再帰性の計算を楽にします。
 
# もし <math>\textstyle\sum^{\infty}_{k=0} a_k</math> が収束する場合、<math> \lim_{s\rightarrow 1^-}\textstyle\sum^{\infty}_{k=0} a_k s^k = \textstyle\sum^{\infty}_{k=0} a^k = a</math>
 
# もし <math>\textstyle\sum^{\infty}_{k=0} a_k</math> が収束する場合、<math> \lim_{s\rightarrow 1^-}\textstyle\sum^{\infty}_{k=0} a_k s^k = \textstyle\sum^{\infty}_{k=0} a^k = a</math>
 
# もし <math> a_k \geq 0, \ \lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{k=0} a_k = a \leq \infty</math> の場合、<math>\textstyle\sum^{\infty}_{k=0} a^k = a</math>
 
# もし <math> a_k \geq 0, \ \lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{k=0} a_k = a \leq \infty</math> の場合、<math>\textstyle\sum^{\infty}_{k=0} a^k = a</math>
Line 101: Line 101:
 
以下の定理の証明はいずれもKarlin & Tayler (1975) を参照してください。
 
以下の定理の証明はいずれもKarlin & Tayler (1975) を参照してください。
  
−
;定理：既約、再帰的、非周期的なマルコフ連鎖は以下を満たす
+
;定理：既約、再帰確実、非周期的なマルコフ連鎖は以下を満たす
  
 
<math>\lim_{n \rightarrow \infty} p^{(n)}_{ij} = 1 / \mu_{jj}</math>
 
<math>\lim_{n \rightarrow \infty} p^{(n)}_{ij} = 1 / \mu_{jj}</math>
Line 107: Line 107:
 
ここで <math>\mu_{jj}</math> は状態 j の平均再帰時間です。i の値に関係ない (j に依存する)値に収束する点に注意します。
 
ここで <math>\mu_{jj}</math> は状態 j の平均再帰時間です。i の値に関係ない (j に依存する)値に収束する点に注意します。
  
−
;定理：既約、再帰的、周期 d のマルコフ連鎖は以下を満たす
+
;定理：既約、再帰確実、周期 d のマルコフ連鎖は以下を満たす
  
 
周期 d を持つ場合、d の倍数にあたる遷移の時だけ
 
周期 d を持つ場合、d の倍数にあたる遷移の時だけ
Line 115: Line 115:
 
それ以外は <math>p^{(m)}_{ii} = 0 \ (m \not= nd)</math> になります。
 
それ以外は <math>p^{(m)}_{ii} = 0 \ (m \not= nd)</math> になります。
  
−
状態 i が正再帰的な場合は <math>\mu_{ii}</math> が有限の値ですが、ゼロ再帰的な場合は無限大、つまり <math>\lim_{n \rightarrow \infty} p^{(n)}_{ii} = 0</math> になります。
+
状態 i が有限再帰な場合は <math>\mu_{ii}</math> が有限の値ですが、ゼロ再帰な場合は無限大、つまり <math>\lim_{n \rightarrow \infty} p^{(n)}_{ii} = 0</math> になります。
  
−
;定理：規約、正再帰的、非周期的なマルコフ連鎖は、定常分布 <math> \bar\pi = (\pi_1, \pi_2, ...) </math> をただ一つ持つ
+
;定理：規約、有限再帰、非周期的なマルコフ連鎖は、定常分布 <math> \bar\pi = (\pi_1, \pi_2, ...) </math> をただ一つ持つ
  
 
<math>\pi_j = \lim_{n \rightarrow \infty} p^{(n)}_{ij} \ (i, j = 1, 2, ...)</math>
 
<math>\pi_j = \lim_{n \rightarrow \infty} p^{(n)}_{ij} \ (i, j = 1, 2, ...)</math>
  
−
マルコフ連鎖は有限でなくても良い点に注意します。定常分布をただ一つ持つような条件を、エルゴード的と呼びます。
+
マルコフ連鎖自体は有限でなくても良い点に注意しましょう。定常分布をただ一つ持つような条件を、エルゴード的と呼びます。
−
状態 i がエルゴード的な時、i は正再帰的、非周期的です。マルコフ連鎖がエルゴード的になるには、全ての状態がエルゴード的かつ規約でなくてはなりません。このとき、確率行列は以下を満たします。
+
状態 i がエルゴード的な時、i は有限再帰、非周期的です。マルコフ連鎖がエルゴード的になるには、全ての状態がエルゴード的かつ規約でなくてはなりません。このとき、確率行列は以下を満たします。
  
 
<math>
 
<math>
Line 139: Line 139:
 
マルコフ連鎖は以下のように分類できます。
 
マルコフ連鎖は以下のように分類できます。
 
# 既約 or 非既約
 
# 既約 or 非既約
−
# 過渡的 or ゼロ再帰的 or 正再帰的
+
# 再帰不確実 or ゼロ再帰 or 有限再帰
 
# 周期的 or 非周期的
 
# 周期的 or 非周期的
  
−
===有限性とゼロ再帰性===
+
===連鎖の有限性とゼロ再帰性===
−
ゼロ再帰性は、有限マルコフ連鎖で生じません。
+
  
−
;定理：有限のマルコフ連鎖における状態は過渡的か正再帰的（ゼロ再帰的な状態は無い）。また、全ての状態が過渡的になることもない
+
ゼロ再帰性は、有限マルコフ連鎖では生じません。
  
−
全ての状態が過渡的である場合、確率行列によって N ステップ後に移動する状態を考えると
+
;定理：有限のマルコフ連鎖における状態は再帰不確実か有限再帰（ゼロ再帰的な状態は無い）。また、全ての状態が再帰不確実になることもない
 +
 
 +
まず全ての状態が再帰不確実である場合を考えます。無限時間後の移動先は確率行列を無限回かけると求められますが、再帰不確実な場合は、全ての状態において遷移確率がゼロに近づいていくはずです。
  
 
<math>\textstyle \lim_{n \rightarrow \infty} \mathbf{P}^{n} = \mathbf{0}</math>
 
<math>\textstyle \lim_{n \rightarrow \infty} \mathbf{P}^{n} = \mathbf{0}</math>
  
−
になってしまうので、'''P''' が確率行列であることと矛盾します。次にゼロ再帰性について考えます。マルコフ連鎖は有限なので、ゼロ再帰的な状態が属す、ゼロ再帰的な同値類 C が存在します。この同値類に対応する確率行列（'''P'''の部分行列）'''P' '''を考えると、ゼロ再帰性からこの部分行列について
+
これは '''P''' が確率行列であることと矛盾します。
 +
 
 +
次にゼロ再帰性について考えます。マルコフ連鎖は有限なので、ゼロ再帰的な状態が属す、有限サイズの同値類 C が存在します。この同値類に対応する確率行列（'''P'''の部分行列）'''P' '''を考えると、ゼロ再帰性から C に属す状態の遷移確率もゼロに近づいていくはずです。
  
 
<math>\textstyle \lim_{n \rightarrow \infty} \mathbf{P'}^{n} = \mathbf{0}</math>
 
<math>\textstyle \lim_{n \rightarrow \infty} \mathbf{P'}^{n} = \mathbf{0}</math>
  
−
でなくてはなりません。しかし C に対応する部分行列も再帰性から確率行列を満たさなくてはならないので、矛盾します。
+
しかし C に対応する部分行列は再帰的ですから確率行列でもあるので、矛盾します。
−
つまり、ゼロ再帰的な状態と過渡的な状態はいずれも <math>\textstyle \lim_{n \rightarrow \infty} p^{(n)}_{ii} = 0</math> を満たすので有限の数で再帰性を満たせないというわけです。
+
つまり、ゼロ再帰的な状態と再帰不確実な状態はいずれも <math>\textstyle \lim_{n \rightarrow \infty} p^{(n)}_{ii} = 0</math> を満たすので有限の状態数で再帰性を満たせないというわけです。
  
−
;定理：有限のマルコフ連鎖に含まれる同値類は、閉じているなら正再帰的
+
;定理：有限のマルコフ連鎖に含まれる同値類は、閉じているなら有限再帰
  
−
正再帰的な状態集合は必ず閉じています。なぜなら閉じていない場合は、いずれかの状態 i において j &rarr; j という集合外への遷移が存在し、状態 i の再帰確率はこの遷移確率 p<sub>ij</sub> 分 1 より少なくなるからです。これは再帰的であることの定義に反します。
+
有限再帰な状態集合は必ず閉じています。なぜなら閉じていない場合は、いずれかの状態 i において j &rarr; j という集合外への遷移が存在し、状態 i の再帰確率はこの遷移確率 p<sub>ij</sub> ぶん 1 より少なくなるからです。これは再帰的であることの定義に反します。
  
−
逆に閉じた同値類が正再帰的でない、つまり過渡的であると仮定します。すると同値類に含まれる状態全てが過渡的になってしまうので、一つ前の定理と同じ理由で矛盾となります。
+
閉じた同値類が有限再帰でない、つまり再帰不確実であると仮定します（ゼロ再帰ではありえない）。すると同値類に含まれる状態全てが再帰不確実のはずです。しかし全てが再帰不確実の場合、同値類の中から集合外への遷移が無くてはなりません。これは閉じていることと矛盾します。
  
 
===正規行列===
 
===正規行列===
−
マルコフ連鎖の世界では、全ての要素が p<sub>ij</sub> > 0 となる確率行列を 正規行列 (regular matrix) と呼ぶことがあります。確率行列が正規な場合、マルコフ連鎖は規約で非周期的（全ての状態間を行き来できる）です。このため正規な確率行列を持つマルコフ連鎖は、正再帰的でもあります。
+
マルコフ連鎖の世界では、全ての要素が p<sub>ij</sub> > 0 となる確率行列を 正規行列 (regular matrix) と呼ぶことがあります。確率行列が正規な場合、マルコフ連鎖は規約で非周期的（全ての状態間を行き来できる）です。このため正規な確率行列を持つマルコフ連鎖は、有限再帰的でもあります。
  
 
ペロン・フロベニウスの定理によると、非負の行列 P が既約であれば
 
ペロン・フロベニウスの定理によると、非負の行列 P が既約であれば
Line 172: Line 175:
 
# 最大固有値に対応する固有ベクトルの成分は、全て正か又は全て負 （当然だが、定常分布は全て正）
 
# 最大固有値に対応する固有ベクトルの成分は、全て正か又は全て負 （当然だが、定常分布は全て正）
  
−
が成立します。つまり最大固有値 1 がただ一つの定常分布に対応するためには、確率行列 P は正規（既約かつ非周期的）でなくてよく、規約なだけで十分です。非周期性は、唯一の定常分布に収束するために必要な条件です。
+
が成立します。つまり最大固有値 1 がただ一つの定常分布に対応するためには、確率行列 P は正規（既約かつ非周期的）でなくてよく、規約なだけで十分です。非周期性は、唯一の定常分布に収束するために必要な条件となります。
  
 
;<big>補足</big>
 
;<big>補足</big>
 
<references/>
 
<references/>

Latest revision as of 07:41, 27 October 2011

Contents

[edit] 再帰時間の母関数

再帰時間と初再帰時間の間には以下の関係が成立します。

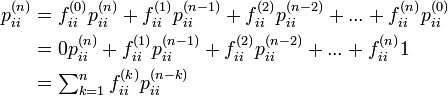
\begin{align} p^{(n)}_{ii} &= f^{(0)}_{ii}p^{(n)}_{ii} + f^{(1)}_{ii}p^{(n-1)}_{ii} + f^{(2)}_{ii}p^{(n-2)}_{ii} + ... + f^{(n)}_{ii}p^{(0)}_{ii} \\ &= 0 p^{(n)}_{ii} + f^{(1)}_{ii}p^{(n-1)}_{ii} + f^{(2)}_{ii}p^{(n-2)}_{ii} + ... + f^{(n)}_{ii} 1 \\ &= \textstyle\sum^{n}_{k=1} f^{(k)}_{ii}p^{(n-k)}_{ii} \end{align}

初通過時間も同様にあらわせます。

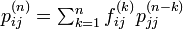
p^{(n)}_{ij} = \textstyle\sum^{n}_{k=1} f^{(k)}_{ij}p^{(n-k)}_{jj}

関数 fij と pij の母関数をそれぞれ Fij(s) と Pij(s) であらわします[1]。

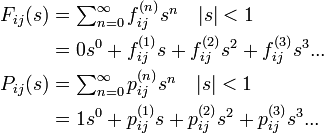
\begin{align} F_{ij}(s) &= \textstyle\sum^{\infty}_{n=0} f^{(n)}_{ij}s^n \quad |s| < 1 \\ &= 0 s^0 + f^{(1)}_{ij} s + f^{(2)}_{ij} s^2 + f^{(3)}_{ij} s^3 ...\\ P_{ij}(s) &= \textstyle\sum^{\infty}_{n=0} p^{(n)}_{ij}s^n \quad |s| < 1 \\ &= 1 s^0 + p^{(1)}_{ij} s + p^{(2)}_{ij} s^2 + p^{(3)}_{ij} s^3 ... \end{align}

(−1, 1) の間に収束する二つの数列の積はやはり(−1, 1) の間に収束することが知られています (Wade 2000)。

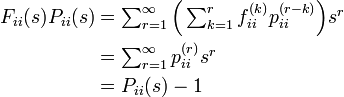
\begin{align} F_{ii}(s) P_{ii}(s) &= \textstyle\sum^{\infty}_{r=1}\Big(\sum^{r}_{k=1}f^{(k)}_{ii}p^{(r-k)}_{ii}\Big) s^r \\ &= \textstyle\sum^{\infty}_{r=1} p^{(r)}_{ii} s^r \\ &= P_{ii}(s) - 1 \end{align}

Pii(s) から 1 を引くのは Fii(s) Pii(s) の第一項が 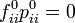f^{0}_{ii} p^{0}_{ii} = 0 であるのに対し Pii(s) の第一項は 1 になるからです。この関係から以下が導かれます。

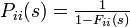
\textstyle P_{ii}(s) = \frac{1}{1 - F_{ii}(s)}

同じようにして、通過時間の母関数に対して

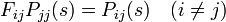
F_{ij}P_{jj}(s) = P_{ij}(s) \quad (i \not= j)

が成立します。こちらは Pij(s) から 1 を引きません。これは Pij(s) の第一項が 1 でなく 0 であることに由来します。

[edit] Abel の収束定理

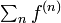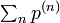以下の定理 (Abelの定理) は証明せずに利用します。この定理と母関数の関係から、再帰性を \textstyle\sum_n f^{(n)} ではなく \textstyle\sum_n p^{(n)} で議論できるようになり、再帰性の計算を楽にします。

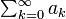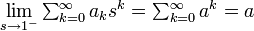
  1. もし \textstyle\sum^{\infty}_{k=0} a_k が収束する場合、 \lim_{s\rightarrow 1^-}\textstyle\sum^{\infty}_{k=0} a_k s^k = \textstyle\sum^{\infty}_{k=0} a^k = a
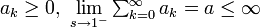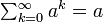
  2. もし a_k \geq 0, \ \lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{k=0} a_k = a \leq \infty の場合、\textstyle\sum^{\infty}_{k=0} a^k = a
定理： 状態 i が再帰確実（不確実）であることと 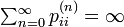\textstyle\sum^{\infty}_{n=0} p^{(n)}_{ii} = \infty は同義

状態 i が再帰確実と仮定します。すなわち

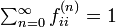
\textstyle\sum^{\infty}_{n=0} f^{(n)}_{ii} = 1

このときAbelの定理から

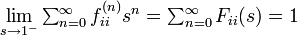
\lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{n=0} f^{(n)}_{ii} s^n = \sum^{\infty}_{n=0} F_{ii}(s) = 1

母関数の関係 P(s) = 1/(1 - F(s)) を用いると

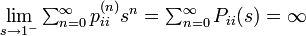
\lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{n=0} p^{(n)}_{ii} s^n = \sum^{\infty}_{n=0} P_{ii}(s) = \infty

したがって再びAbelの定理から 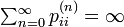\textstyle\sum^{\infty}_{n=0} p^{(n)}_{ii} = \infty となります。

逆方向は背理法で示します。 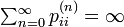\textstyle\sum^{\infty}_{n=0} p^{(n)}_{ii} = \infty のときに状態 i が再帰不確実 (transient) と仮定します。このときAbelの定理から

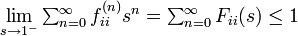
\lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{n=0} f^{(n)}_{ii} s^n = \sum^{\infty}_{n=0} F_{ii}(s) \leq 1

母関数の関係 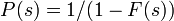P(s) = 1/(1 - F(s)) を用いると

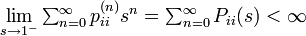
\lim_{s\rightarrow 1^-} \textstyle\sum^{\infty}_{n=0} p^{(n)}_{ii} s^n = \sum^{\infty}_{n=0} P_{ii}(s) < \infty

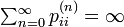これは \textstyle\sum^{\infty}_{n=0} p^{(n)}_{ii} = \infty と矛盾するので定理が証明できました。

補題：同じ同値類に属する状態は、再帰性に関する性質が等しい

状態 i, j が同じ同値類に属すと仮定し、m,n ステップでそれぞれ i → j, j → i の遷移が可能とします。すなわち 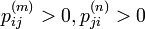p^{(m)}_{ij} > 0, p^{(n)}_{ji} > 0 です。

状態 i が再帰確実 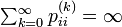\textstyle\sum^{\infty}_{k=0} p^{(k)}_{ii}= \infty と仮定します。状態 j について以下が成立するので、j もやはり再帰確実です。

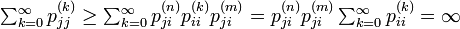
\textstyle\sum^{\infty}_{k=0} p^{(k)}_{jj} \geq \sum^{\infty}_{k=0} p^{(n)}_{ji} p^{(k)}_{ii} p^{(m)}_{ji} = p^{(n)}_{ji} p^{(m)}_{ji} \sum^{\infty}_{k=0} p^{(k)}_{ii} = \infty

状態 i が再帰確実でなければ、i は不確実です。そのため同じ同値類に属す状態集合は、全て再帰確実か、すべて不確実のどちらかです。

[edit] 定常分布の極限定理

以下の定理の証明はいずれもKarlin & Tayler (1975) を参照してください。

定理：既約、再帰確実、非周期的なマルコフ連鎖は以下を満たす

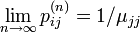
\lim_{n \rightarrow \infty} p^{(n)}_{ij} = 1 / \mu_{jj}

ここで 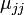\mu_{jj} は状態 j の平均再帰時間です。i の値に関係ない (j に依存する)値に収束する点に注意します。

定理：既約、再帰確実、周期 d のマルコフ連鎖は以下を満たす

周期 d を持つ場合、d の倍数にあたる遷移の時だけ

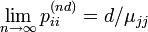
\lim_{n \rightarrow \infty} p^{(nd)}_{ii} = d / \mu_{jj}

それ以外は 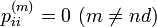p^{(m)}_{ii} = 0 \ (m \not= nd) になります。

状態 i が有限再帰な場合は 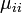\mu_{ii} が有限の値ですが、ゼロ再帰な場合は無限大、つまり 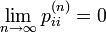\lim_{n \rightarrow \infty} p^{(n)}_{ii} = 0 になります。

定理：規約、有限再帰、非周期的なマルコフ連鎖は、定常分布 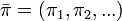\bar\pi = (\pi_1, \pi_2, ...) をただ一つ持つ

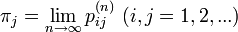
\pi_j = \lim_{n \rightarrow \infty} p^{(n)}_{ij} \ (i, j = 1, 2, ...)

マルコフ連鎖自体は有限でなくても良い点に注意しましょう。定常分布をただ一つ持つような条件を、エルゴード的と呼びます。 状態 i がエルゴード的な時、i は有限再帰、非周期的です。マルコフ連鎖がエルゴード的になるには、全ての状態がエルゴード的かつ規約でなくてはなりません。このとき、確率行列は以下を満たします。

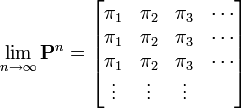
\lim_{n \rightarrow \infty} \mathbf{P}^{n} = \begin{bmatrix} \pi_1 & \pi_2 & \pi_3 & \cdots \\ \pi_1 & \pi_2 & \pi_3 & \cdots \\ \pi_1 & \pi_2 & \pi_3 & \cdots \\ \vdots & \vdots & \vdots & \\ \end{bmatrix}

つまり初期値に依存しない値になります。上の定理とあわせると、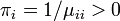\ \pi_i = 1/\mu_{ii} > 0 が導かれます。

[edit] マルコフ連鎖の分類

マルコフ連鎖は以下のように分類できます。

  1. 既約 or 非既約
  2. 再帰不確実 or ゼロ再帰 or 有限再帰
  3. 周期的 or 非周期的

[edit] 連鎖の有限性とゼロ再帰性

ゼロ再帰性は、有限マルコフ連鎖では生じません。

定理：有限のマルコフ連鎖における状態は再帰不確実か有限再帰（ゼロ再帰的な状態は無い）。また、全ての状態が再帰不確実になることもない

まず全ての状態が再帰不確実である場合を考えます。無限時間後の移動先は確率行列を無限回かけると求められますが、再帰不確実な場合は、全ての状態において遷移確率がゼロに近づいていくはずです。

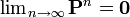
\textstyle \lim_{n \rightarrow \infty} \mathbf{P}^{n} = \mathbf{0}

これは P が確率行列であることと矛盾します。

次にゼロ再帰性について考えます。マルコフ連鎖は有限なので、ゼロ再帰的な状態が属す、有限サイズの同値類 C が存在します。この同値類に対応する確率行列（Pの部分行列）P' を考えると、ゼロ再帰性から C に属す状態の遷移確率もゼロに近づいていくはずです。

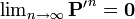
\textstyle \lim_{n \rightarrow \infty} \mathbf{P'}^{n} = \mathbf{0}

しかし C に対応する部分行列は再帰的ですから確率行列でもあるので、矛盾します。 つまり、ゼロ再帰的な状態と再帰不確実な状態はいずれも 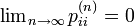\textstyle \lim_{n \rightarrow \infty} p^{(n)}_{ii} = 0 を満たすので有限の状態数で再帰性を満たせないというわけです。

定理：有限のマルコフ連鎖に含まれる同値類は、閉じているなら有限再帰

有限再帰な状態集合は必ず閉じています。なぜなら閉じていない場合は、いずれかの状態 i において j → j という集合外への遷移が存在し、状態 i の再帰確率はこの遷移確率 pij ぶん 1 より少なくなるからです。これは再帰的であることの定義に反します。

閉じた同値類が有限再帰でない、つまり再帰不確実であると仮定します（ゼロ再帰ではありえない）。すると同値類に含まれる状態全てが再帰不確実のはずです。しかし全てが再帰不確実の場合、同値類の中から集合外への遷移が無くてはなりません。これは閉じていることと矛盾します。

[edit] 正規行列

マルコフ連鎖の世界では、全ての要素が pij > 0 となる確率行列を 正規行列 (regular matrix) と呼ぶことがあります。確率行列が正規な場合、マルコフ連鎖は規約で非周期的（全ての状態間を行き来できる）です。このため正規な確率行列を持つマルコフ連鎖は、有限再帰的でもあります。

ペロン・フロベニウスの定理によると、非負の行列 P が既約であれば

  1. 最大固有値は正で、かつ、実数　（ 1 が最大固有値）
  2. 最大固有値は、Ａの固有方程式の単純根 （定常分布はただ一つであることに対応）
  3. 最大固有値に対応する固有ベクトルの成分は、全て正か又は全て負 （当然だが、定常分布は全て正）

が成立します。つまり最大固有値 1 がただ一つの定常分布に対応するためには、確率行列 P は正規（既約かつ非周期的）でなくてよく、規約なだけで十分です。非周期性は、唯一の定常分布に収束するために必要な条件となります。

補足
  1. ↑ fij と pijは一時的 (transient) かもしれないため総和は 1 以下の可能性があります。したがって確率母関数にはなっていません。
Retrieved from "http://metabolomics.jp/mediawiki/index.php?title=Aritalab:Lecture/NetworkBiology/Markov_Chains/StationaryDistribution&oldid=255147"
Personal tools
Namespaces

Variants
Actions
Navigation
metabolites
Toolbox