Aritalab:Lecture/Algorithm/Reducibility

問題の変換

SAT問題がNP完全であることが証明されれば、他のNP完全問題をみつけることは楽になります。ある問題がNP完全であることを示すには

クラス NP に属する
その問題がNP完全の問題を部分問題として含んでいる

ことを示せばよいだけです。

ここでは、3SAT → 3DM → Partition, Exact Cover, 3SAT → Vertex Cover → Hamiltonian Circuit という順番でNP完全問題を紹介します。この順番は 1972 年に Richard M Karp が 21 個のNP完全問題を変換した論文 "Reducibility Among Combinatorial Problems" (In RE Miller and JW Thatcher (eds) Complexity of Computer Computations. Plenum (New York) pp. 85–103 に基づいています。

Garey & Johnson の教科書も参考にしてください。

Three Dimensional Matching (3DM)

三次元マッチング (3-dimensional matching; 3DM) は、マッチング問題（または結婚問題）と呼ばれる有名な組み合わせ問題の三次元版です。

問題: サイズのひとしい集合 W, X, Y から一つずつ要素を取り出して作った三つ組の集合 E ⊆ W × X × Y が与えられた時、Eの中から |W| 組を取り出して、W, X, Y のいずれの要素も取りこぼしや重複なく選ぶことができるか。

例: W = { A, B, C }; X = { a, b, c }; Y = { 1, 2, 3 };

E = (A, a, 1), (A, a, 3), (B, a, 1), (B, a, 3), (B, b, 1), (B, c, 2), (C, c, 2)

この問題の解は (A, b, 1) (B, a, 3) (C, c, 2) で、W, X, Y の要素がそれぞれ1度ずつ使われています。

3DM はNP完全

正解となる組を与えられたら、集合 W, X, Y の要素が全て重複なく使われているかどうかはすぐに判定できるので 3DM ∈ NP です。これから 3SAT問題を3DM問題に変換しましょう。3SAT問題は変数 { u₁, u₂, ... , u_n } を用いた節集合 C = { c₁, c₂, ... , c_m } で構成されるとします。

三つ組の集合 M は、真偽値の設定用、充足性判定用、ガーベッジコレクション用の 3 タイプ用意します。

真偽値の設定用

3SATに登場する各変数 u に対し、節の数 m 個に対応する以下のマッチングモジュール M を用意します。

M_u^T = { (¬u[k], a[k], b[k]): 1 ≤ k ≤ m }

M_u^F = { (u[k], a[k+1], b[k]): 1 ≤ k < m } ∪ { u[m], a[1], b[m] }

ここで変数 a, b は変数 u を3DMに変換するために用いるもので、各 u の変換にしか登場しません。このユニットをみたすマッチングは、M^T に対応する m 個の三つ組を選択するか、M^F に対応する m 個を選択するかしかありません。つまり、変数 u を T か F のどちらかに設定できます。3SATを充足するアサインメントで変数 u が T のとき、M^T の三つ組 ( m 個) を選択します。変数 u が F のときは M^F を選択します。

充足性判定用

充足性判定用のマッチングモジュールは、m 個ある各節 c 毎に用意します。節 c に出てくる変数が (u_i, u_j, u_k) だとすると

M_c: { u_i, s₁, s₂ } ∪ { u_j, s₁, s₂ } ∪ { u_k, s₁, s₂ }

を用意します。（もし節の中で ¬u_i という使われ方をしていたら、{ ¬u_i, s₁, s₂ } という組をつくります。）ここでs₁, s₂は変換用の変数で、節 c を特定するために用います。各節を充足するには T となる要素が必ず一つは存在するので、その要素が s₁, s₂ とマッチングするように三つ組を選びます。

ガーベッジコレクション用

充足性判定の部分では、各節において一つだけ T とする変数を選んでおり、残りを使いません。充足に使われなかった残りのリテラルは、ガーベッジコレクション用の三つ組で利用します。ガーベッジコレクションの三つ組は専用の変数 g₁, g₂ を用いて

G_k: { (u[j], g₁[k], g₂[k]), (¬u[j], g₁[k], g₂[k]): 1 ≤ j ≤ m, 1 ≤ k ≤ m(n−1) }

と定義します。3SATに出現する変数に対応する真偽値設定用の要素は 2nm 個あります。そのうち、真偽値設定モジュールで半数を利用するので、残りは nm 個です。そのうち、充足性判定用に各節から 1 つずつ、合計 m 個の要素を使います。残った m(n−1) 個をガーベッジコレクションするので、 g₁[k], g₂[k]を 1 ≤ k ≤ m(n−1) 個用意し、それぞれについて、nm 個あるどの変数でもガーベッジコレクトできるようにします。

3SAT→3DMの例

3SAT 問題 (x ∨ y ∨ z) ∧ (¬ x ∨ ¬y ∨ z) を変換します。変数は x, y, z 、節の数は2つなので以下の真偽値設定モジュールを用意します。赤く示してあるのは、¬x, y, z を T に設定する時に選択する三つ組で、それぞれ M_x^F, M_y^T, M_z^T に対応します。

変数 x:	(x[1], b[1], a[2])	(¬x[1], a[1], b[1])	(x[2], b[2], a[1])	(¬x[2], a[2], b[2])
変数 y:	(¬y[1], c[1], d[1])	(y[1], d[1], c[2])	(¬y[2], c[2], d[2])	(y[2], d[2], c[1])
変数 z:	(¬z[1], e[1], f[1])	(z[1], f[1], e[2])	(¬z[2], e[2], f[2])	(z[2], f[2], e[1])

また二つの節に対応する充足判定モジュールを用意します。ここでは ¬x, y を T とするので赤字で示した三つ組を選択します。（他の選択方法もあります。）

M_c1:	(x[1], s₁, s₂)	(y[1], s₁, s₂)	(z[1], s₁, s₂)
M_c2:	(¬x[2], t₁, t₂)	(y[2], t₁, t₂)	(z[2], t₁, t₂)

最後に、節を T にするのに利用しなかった要素 x[1], y[2], z[1], z[2] がマッチングから外れているのでこれらをガーベッジコレクションします。

G₁:	(x[1], g₁[1], g₂[1])	(¬x[1], g₁[1], g₂[1])	(x[2], g₁[1], g₂[1])	(¬x[2], g₁[1], g₂[1])
	(y[1], g₁[1], g₂[1])	(¬y[1], g₁[1], g₂[1])	(y[2], g₁[1], g₂[1])	(¬y[2], g₁[1], g₂[1])
	(z[1], g₁[1], g₂[1])	(¬z[1], g₁[1], g₂[1])	(z[2], g₁[1], g₂[1])	(¬z[2], g₁[1], g₂[1])
G₂:	(x[1], g₁[2], g₂[2])	(¬x[1], g₁[2], g₂[2])	(x[2], g₁[2], g₂[2])	(¬x[2], g₁[2], g₂[2])
	(y[1], g₁[2], g₂[2])	(¬y[1], g₁[2], g₂[2])	(y[2], g₁[2], g₂[2])	(¬y[2], g₁[2], g₂[2])
	(z[1], g₁[2], g₂[2])	(¬z[1], g₁[2], g₂[2])	(z[2], g₁[2], g₂[2])	(¬z[2], g₁[2], g₂[2])
G₃:	(x[1], g₁[3], g₂[3])	(¬x[1], g₁[3], g₂[3])	(x[2], g₁[3], g₂[3])	(¬x[2], g₁[3], g₂[3])
	(y[1], g₁[3], g₂[3])	(¬y[1], g₁[3], g₂[3])	(y[2], g₁[3], g₂[3])	(¬y[2], g₁[3], g₂[3])
	(z[1], g₁[3], g₂[3])	(¬z[1], g₁[3], g₂[3])	(z[2], g₁[3], g₂[3])	(¬z[2], g₁[3], g₂[3])
G_m(n−1):	(x[1], g₁[4], g₂[4])	(¬x[1], g₁[4], g₂[4])	(x[2], g₁[4], g₂[4])	(¬x[2], g₁[4], g₂[4])
	(y[1], g₁[4], g₂[4])	(¬y[1], g₁[4], g₂[4])	(y[2], g₁[4], g₂[4])	(¬y[2], g₁[4], g₂[4])
	(z[1], g₁[4], g₂[4])	(¬z[1], g₁[4], g₂[4])	(z[2], g₁[4], g₂[4])	(¬z[2], g₁[4], g₂[4])

まとめると、m 節　n 変数の 3SAT 問題は、2mn + 3m + 2mn × m(n−1) 組からなる 3DM 問題に変換されることがわかります。 3SAT を充足可能とする変数のアサインメントに従えば 3DM の解を構成でき、逆に 3DM の解となる三つ組を選択すると、 3SAT を充足します。

Partition

二分割 (partition) 問題は以下のように定義されます。

集合 A の各要素 a ∈ A に重さ s(a) ∈ Z⁺ が定義されているとき、総重量がちょうど半分になる A の部分集合 A' ⊂ A が存在するか。

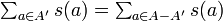
$\textstyle\sum_{a \in A'} s(a) = \sum_{a \in A - A'} s(a)$

集合 A の要素の総和 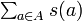$\textstyle\sum_{a \in A} s(a)$ が奇数だったら直ちに NO と言えますし、重さ順に並べてバランスをとればうまく解けそうな問題に見えますが、これから二分割問題で 3DM 問題を表現できる（部分問題として含む）ことを示します。

二分割問題はNP完全

W, X, Y のサイズが q, 三つ組の集合 E が要素を k 個含む 3DM 問題を考えます。まず E に含まれる各要素を 3q 桁からなる数字で表現します。要素を e = { w_h, x_i, y_j } (1 ≤ h, i, j ≤ q) と書くと、この三つ組 e に対応する数字 f(e) は初めの q 桁のうち h 番目だけ 1 にして残りを 0、真ん中の q 桁のうち i 番目だけ 1 にして残りを 0、最後の q 桁のうち j 番目だけ 1 にして残りを 0 にしたものです。E の部分集合で 3DM を作れる場合、マッチングに対応する要素の数字を全部足し合わせた数は、3q 桁全てを 1 にした数に等しくなります。この、全桁が 1 である数を B とおきましょう。また全数字の和を 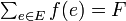$\textstyle\sum_{e \in E} f(e) = F$ とおきます。

二分割問題で用いる集合は、E に含まれる各要素 e を数字に変換した f(e) の値 k 個と、f₁ = 2F - B, f₂ = F + B からなる k + 2 個で構成します。これらの数字を全て足し合わせた値は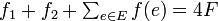 $f_1 + f_2 + \textstyle\sum_{e \in E} f(e) = 4 F$ ですから、E の部分集合を選んでちょうど二分割できた場合、その総和は 2F です。このとき、f₁, f₂ の両方を含むことはできず、どちらか片方のみ含みます。そのとき、f₁ または f₂ 以外の要素の和はちょうど B になり、 3DM を構成しています。

二分割問題は明らかにNPに属しています。数字への変換手続きは 3DM の問題サイズに比例する時間で可能です。また E の大きさが k の場合、例えば W の要素 w_i が最大 k 回現れる可能性があるため、数字に変換するときに (k+1) 進数を用います。そうすると総和である F を計算するときに桁の繰り上げが起きないので要素間で個数が影響することがありません。

まとめると、W, X, Y のサイズが q、三つ組が k 個ある 3DM 問題が与えられたら、(k+1)進数で表現した 3q 桁の数字 k + 2 個を用いた二分割問題に変換することができました。

3DM → Partition の例

例として以下の 3DM 問題を二分割問題に変換しましょう。

W = { A, B, C }; X = { a, b, c }; Y = { 1, 2, 3 };

E = (A, b, 1), (A, a, 3), (B, a, 1), (B, a, 3), (B, b, 1), (B, c, 2), (C, c, 2)

W, X, Y のサイズが 3 なので 3 × 3 = 9 桁の数に変換します。

E	WXY 3桁ずつ
(A, b, 1)	100 010 100
(A, a, 3)	100 100 001
(B, a, 1)	010 100 100
(B, a, 3)	010 100 001
(B, b, 1)	010 010 100
(B, c, 2)	010 001 010
(C, c, 2)	001 001 010
総計 F	241 322 322

二分割問題は上の表にある 7 つの数に加えて、2F - 111 111 111 = 371 533 533 と、F + 111111111 = 352 433 433 の二つを加えた 9 つで構成されます。分割の解は

100 010 100 + 010 100 001 + 001 001 010 + 371 533 533 = 100 100 001 + 010 100 100 + 010 010 100 + 010 001 010 + 352 433 433

でありマッチング (A, b, 1) (B, a, 3) (C, c, 2) に相当します。

Set Cover

3DM は集合の被覆問題と考えることができます。以下の Exact Cover by 3-Sets (X3C) 問題は、3DM 問題を一般化した形になっています。

X3C: サイズが 3q の集合 X と、X の要素の三つ組の集合 C に対し、部分集合 C' ⊂ C で X の全ての要素がちょうど 1 回だけ現れるものがあるか。

X3Cにおいて、集合 X を 3つ (W ∪ X ∪ Y) に分けて各集合から 1 つずつ選ぶように制限した場合が 3DM になっています。つまりX3Cの部分問題が 3DM になるので X3C は NP 完全です。さらに問題を一般化しましょう。

Exact Cover (EC): 集合 X と、X の部分集合の集合 C に対し、部分集合 C' ⊂ C で X の全ての要素がちょうど 1 回だけ現れるものがあるか。

EC において部分集合の大きさを 3 に限定した場合が X3C になっています。そのため EC も NP 完全です。Exact Cover は Hitting Set と呼ばれる問題と等価であり、ここから数独 (Sudoku) 問題の NP 完全性が示せます。さらに問題を一般化しましょう。

Set Cover (SC): 集合 X と、X の部分集合の集合 C に対し、部分集合 C' ⊂ C で X の全ての要素が 1 回以上現れるものがあるか。

集合被覆問題 SC において、各要素の出現回数を 1 回に限った場合が EC になっています。そのため SC も NP 完全です。

グラフに関連するNP完全問題

グラフに関連するNP完全問題の多くは頂点被覆 (Vertex Cover)、独立点集合 (Independent Set)、クリーク (Clique) の概念から出発します。

頂点被覆問題 (VC)

グラフ G = (V,E) と正整数 K ≤ |V| に対し、|V'| ≤ K かつ V' ⊂ V で、どの辺 {u,v} ∈ E も u, v のどちらか（または両方）が含まれるような頂点の部分集合 V' が存在するか。

独立点集合 (IS)

グラフ G = (V,E) と正整数 K ≤ |V| に対し、|V'| ≥ K かつ V' ⊂ V で、どの辺 {u,v} ∈ E も u, v が同時に V' に含まれないような頂点の部分集合 V' が存在するか。

クリーク (Clique)

グラフ G = (V,E) と正整数 K ≤ |V| に対し、|V'| ≥ K かつ V' ⊂ V で、 V' の頂点間には必ず辺が存在するような頂点の部分集合 V' が存在するか。

これらの問題は等価で、以下の関係が成り立ちます。

V' がグラフ G の頂点被覆
V − V' がグラフ G の独立点集合
V − V' がグラフ G^C のクリーク

ここで G^C は G の補グラフで、G の頂点間で辺をひく場合とひかない場合を逆にしたものを意味します。以下に 3SAT → VC → Hamiltonian Circuit (HC) の順に NP 完全性を示しますが、自明な変換から IS や Clique 問題も NP 完全であることがわかります。

Vertex Cover (VC)

VC は NP完全

3SAT 問題が、VC で表現できることを示します。n 変数 U = { u₁, u₂, ... u_n }、m 個の節 C = { c₁, c₂, ... c_m } からなる 3SAT 問題が与えられたと仮定します。各変数 u_i に対して

(u)――(¬u)

という 2 頂点からなるユニットを n 組用意します。各節 c_i = { a, b, c } に対して

     (a[i])
     ／   ＼
   ／　　　 ＼
(b[i])――(c[i])

という 3 頂点からなる三角形のユニットを m 組用意します。（最後の (a) は最初の (a) と結ぶことを意味しています。） a, b, c はそれぞれ変数 u_x かその否定形 ¬ u_x が入るので、各頂点を対応する変数ユニットの頂点と結んでおきます。

こうして n 変数 m 節の 3SAT 問題が、2n + 3m 頂点、n + 3m 辺の VC 問題になりました。ここで K = n + 2m に設定します。3SAT 問題を充足する変数の真偽値割り当てがある場合、変数ユニットから充足する割り当ての頂点を n 個選び、各三角ユニットからは F（偽）になってもよいリテラルに対応する部分を二つずつ 2m 個選びます。そうすると変数ユニットの辺も、三角ユニットの辺も全て被覆されるのでサイズが (n + 2m) の解になっています。

逆に、VC 問題の解となる頂点被覆を考えてみます。各変数ユニットでは少なくとも片方が選ばれないと辺をカバーできませんし、各三角ユニットでは少なくとも二つの頂点が選ばれないと、ユニットの辺をカバーできません。ですから、少なくとも n + 2m の頂点が必要です。そのような頂点被覆があれば、変数ユニットの頂点を選んだとおりに真偽値を割り当てて 3SAT を充足できます。

まとめると、いかなる 3SAT 問題とも等価の VC 問題を問題サイズに比例する時間で構築できるので、VC も NP 完全問題に属します。

Hamiltonian Circuit (HC)

ハミルトン回路とはグラフ中の全頂点をちょうど一回ずつまわって元に戻る経路のことです。始点や終点を指定せず、グラフ中を一周する経路の有無を判断します。

HC: グラフ G = (V,E) に含まれる n = |V| 頂点の並び順 { v₁, v₂, ..., v_n } で { v_i, v_i+1 } ∈ E (1 ≤ i ≤ n-1) かつ { v_n, v₁ } ∈ E となるものがあるか

HC は NP完全

VC を HC に変換しましょう。与えられたグラフ G=(V,E) と頂点被覆のサイズ K に対し、ハミルトン回路問題のグラフ G' を構築します。G' はサイズ K 選択ユニットと辺ユニットの二種類から構築されます。

選択ユニット

|V| 個ある頂点から　K 個を選ぶためのユニットです。頂点を K 個 { a₁, a₂, ... a_k } 用意します。

辺ユニット

グラフ G の各辺 (u,v) ∈ E を 12 頂点 14 辺からなるユニットで置き換えます。（図が必要）このユニットの目的を理解するため、まずは簡単な 4 頂点 4 辺からなる正方形ユニットで考えます。

(u)――(u')
 |      |
(v)――(v')

そして G の各頂点 u ∈ V について、u に接続する辺 e₁, e₂, ..., e_k ∈ E に対応する正方形ユニットのうち、u 側を以下のようにつなぎます。ここで k = deg(v) は v の次数です。

(u1)――(u1')――(u2)――(u2')―― ... ―― (uk)――(uk')
 |       |        |       |                  |       |
(v1)――(v1')    (v2)――(v2')              (vk)――(vk')

さらに u1 と uk' の 2 頂点だけは、K 個の選択ユニット全てと接続します。ある選択ユニットから u1 にやってきた場合、以下のように全ての u, u', v, v' 頂点を廻ってもよいし

(u1)――(u1')━━(u2)――(u2')━━ ... ━━ (uk)――(uk')
 ┃      ┃       ┃      ┃                 ┃      ┃
(v1)━━(v1')    (v2)━━(v2')              (vk)━━(vk')

u 側だけを廻ることもできます。

(u1)━━(u1')━━(u2)━━(u2')━━ ... ━━ (uk)━━(uk')
 |       |        |       |                  |       |
(v1)――(v1')    (v2)――(v2')              (vk)――(vk')

正方形の辺ユニットそれぞれにおいて、表現する辺の片側だけが頂点被覆に選ばれている場合はジグザグに進んで4点を網羅し、辺の両端が頂点被覆に含まれている場合は、u 側と v 側を別々に通る経路とする仕組みです。

この変換により G' を構築した場合、グラフ G の頂点被覆に対応する選択ユニットから被覆する辺を辿ることでハミルトン回路を構成できることがわかります。逆にハミルトン回路が出来ている場合、選択ユニットはある順序で全て使われており、選択ユニットの間は K 個の辺ユニットでつながっているはずです。辺ユニットのつながりはそれぞれ1個の頂点に対応するため、K 個の VC を特定できる訳です。

この条件を正確に満たすためには、辺ユニットに u 側から入ってユニットの頂点をカバーしながら抜けると必ず u 側から出る（v 側からでない）仕組みが必要です。ここで上記の正方形ユニットは不適切となります。なぜなら

(u)――(u')
 ┃     ┃
(v)――(v')

という通り方を許してしまうからです。これを不可能にするためには、初めに述べた 12 頂点 14 辺からなるユニットを用いる必要があります。VC におけるグラフ G = (V,E) と正整数 K は、頂点数 K + 12 × |E|、辺数 K × 2|E| + 14 × |E| + (2 |E| − |V|) のグラフ G' に変換されることになります。

この変換は多項式時間で終了するため、HC はNP完全となります。全く同じ変換で、回路になっていないハミルトン問題も VC を包含することがわかります。

Longest Path

最短経路問題 (Shortest Path) はダイクストラ法などで効率よく解けることが知られています（クラスP）が、最長経路問題 (Longest Path) は NP 完全です。

グラフ G=(V,E)と正整数 K ≤ |V| に対し、K 本以上の辺を使ってどの頂点も 2 回以上通らない経路があるか

この問題は、K = |V| と制限した時にハミルトン経路問題になってしまいます。

Aritalab:Lecture/Algorithm/Reducibility

Contents

問題の変換

Three Dimensional Matching (3DM)

3SAT→3DMの例

Partition

3DM → Partition の例

Set Cover

グラフに関連するNP完全問題

Vertex Cover (VC)

Hamiltonian Circuit (HC)

Longest Path

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

metabolites

Toolbox