Aritalab:Lecture/NetworkBiology/Zipf
Contents |
Zipf の法則とランク・サイズ則
都市毎の人口や会社の規模、個人の所得を大きさの順に並べて順位 r をつけ、その大きさを 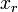 とおくと
とおくと
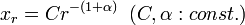
の形になります(α の値は小さい)。一般には Zipf の法則として知られる関係は、Rank-Size Rule とも呼ばれます。
ランダムな区画取り
ランダムに 2 点をとったとき、 2 点間の距離の分布
線分 [0,1] 上にランダムにとる点を y とします。 y から距離 x と x + dx の間に 2 点目を取る確率を計算しましょう。
- 0 または 1 から幅 x 以内に y をとるとき (確率 2 x)
y から x 離れた地点は片側にしかとることができません。2 番目の点が x と x + dx の間に落ちる確率は 2x dx です。
- 残りの範囲に y をとるとき (確率 1 - 2x)
y から x 離れた地点を両側にとれます。2 番目の点が x と x + dx の間に落ちる確率は 2(1-2x) dx です。
結局、2 点間の距離の確率は以下のようになります。
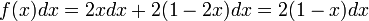
平均値は 1/3 です。
ランダムに 2 点をとる作業を n 回繰り返したとき、r 番目の距離の分布
ランダムにとった区間長が w より長い確率 p 、短い確率 q はそれぞれ以下のようになります。
n 回繰り返したときに、r 番目に長い区間が x である確率 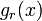 は r − 1 個が x より長く、n − r 個が、より短い区間であることに相当します。
は r − 1 個が x より長く、n − r 個が、より短い区間であることに相当します。
期待値を計算するのに 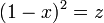 と変数変換します。
微分すると
と変数変換します。
微分すると 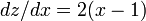 です。
です。
- 一番長い区間の期待値
![\begin{align}
E[g_1(x)] &= 1 - n! \cdot \frac{\Gamma(\frac{3}{2})}{\Gamma(n + \frac{3}{2})} \\
&= 1 - \frac{\sqrt{\pi}}{2} \frac{n!}{\Gamma(n + \frac{3}{2})}
\end{align}](/mediawiki/images/math/e/7/2/e72856e5ed4b724f53da45c67a9749d8.png)
- 一番短い区間の期待値
![\begin{align}
E[g_n(x)] &= 1 - n \cdot \frac{\Gamma(n+\frac{1}{2})}{\Gamma(n+\frac{3}{2})}\\
&= 1 - \frac{2n}{2n+1}
\end{align}](/mediawiki/images/math/d/4/7/d472faa6c8d6cd01256ec50f98e3c2be.png)
ランダムな分割
線分を s 個に分割した時の長さの期待値
まず、線分 [0,1] を 3 個に分割する場合を考えます。ランダムに 2 点を取ったとき、任意に選んだ断片の長さが x である確率を 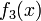 とします。一般性を失わずにこの断片が左端とします。2 点のうち、1 つは x の位置に固定し (2 通り)、残りは (1 − x) の中から選べます。
とします。一般性を失わずにこの断片が左端とします。2 点のうち、1 つは x の位置に固定し (2 通り)、残りは (1 − x) の中から選べます。
この値は、ランダムに 2 点を取ったときの二点間の距離に等しくなっていて、長さの期待値は 1/3 です。
ランダムに s 点を取るときも同様に考えます。s 点のうち 1 つを x の位置に固定し、残りは (1 − x) の中から選びます。s 個に分割するとき、任意に選んだ断片の長さが x になる確率は
期待値は
線分を s 個に分割した時の長さの差の期待値
線分 [0,1] をランダムに s 分割するとき、得られる線分の長さを短いものから長いものに並べ替えて 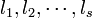 と書きましょう。ここで
と書きましょう。ここで 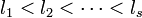 また
また 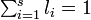 です。
です。
ここで r 番目の線分と r+1 番目の線分の差を 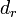 と書きます。
と書きます。
このとき 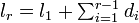 です。全ての線分を足し合わせると長さは 1 になります。
です。全ての線分を足し合わせると長さは 1 になります。
ここで、新たに 1 点を追加する過程を考えましょう。ランダムに追加する 1 点は 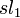 の確率で( s + 1 個に増えたときに)最短の線分を作り、
の確率で( s + 1 個に増えたときに)最短の線分を作り、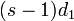 の確率で 2 番目に短い線分を作り、
の確率で 2 番目に短い線分を作り、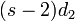 の確率で 3 番目に短い線分を作ります。しかし、どの線分も全て等確率で生じるはずなので、結果として以下が成立します。
の確率で 3 番目に短い線分を作ります。しかし、どの線分も全て等確率で生じるはずなので、結果として以下が成立します。
ここから
線分を s 個に分割してから順位づけした時の期待値
線分の差である di の期待値から、初めに仮定した l の期待値を求めましょう。 短い方から i 番目の長さは
同様に、長いほうから順番に並べた場合は i 番目の長さは
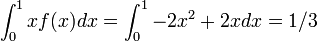
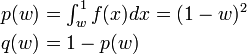
![\begin{align}
g_r(x) &= \frac{n!}{(n-r)!(r-1)!}p(x)^{r-1}q(x)^{n-r} f(x) \\
&= \frac{n!}{(n-r)!(r-1)!} (1 - x)^{2(r-1)}[1-(1 - x)^2]^{n-r} \cdot 2(1-x)
\end{align}](/mediawiki/images/math/2/1/a/21a5acc6a71f28b460b96f61ba6d9627.png)
![\begin{align}
E[g_r(x)] &= \int^1_0 x g_r(x) dx\\
&= \frac{n!}{(n-r)!(r-1)!} \int^0_1 (1-z^{1/2}) z^{r-1}(1-z)^{n-r} \cdot 2(1-x) dz (dx/dz) \\
&= \frac{n!}{(n-r)!(r-1)!} \int^1_0 (1-z^{1/2}) z^{r-1}(1-z)^{n-r} dz \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \int^1_0 z^{r-1}(1-z)^{n-r} dz - \int^1_0 z^{r-1/2}(1-z)^{n-r} dz\big] \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \frac{\Gamma(r)\Gamma(n-r+1)}{\Gamma(n+1)} - \frac{\Gamma(r+\frac{1}{2})\Gamma(n-r+1)}{\Gamma(n+\frac{3}{2})} \big] \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \frac{(r-1)!(n-r)!}{n!} - \frac{\Gamma(r+\frac{1}{2})}{\Gamma(n+\frac{3}{2})} (n-r)! \big] \\
&= 1 - \frac{n!}{(r-1)!}\frac{\Gamma(r+\frac{1}{2})}{\Gamma(n+\frac{3}{2})}
\end{align}](/mediawiki/images/math/7/1/f/71fb00f40ac1572866540a0709d2ce74.png)
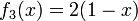
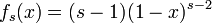
![\int^1_0 x f_s(x) dx = - \int^1_0 (1-x)^{s-1} dx
= - \frac{1}{s} \Big[ (1-x)^s \Big]^1_0 = \frac{1}{s}](/mediawiki/images/math/4/6/9/469b637c445920c3868d2c77d46cc1ad.png)
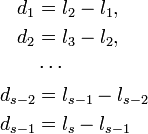
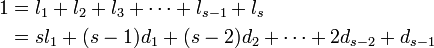
![\textstyle
E[sl_1] = E[(s-1)d_1] = E[(s-2)d_2] = \cdots = E[d_{s-1}] = \frac{1}{s}](/mediawiki/images/math/4/f/a/4fae007bb24f0a2e5c0a2fbf437b6c70.png)
![\textstyle
E[l_1] = \frac{1}{s^2},\ E[d_1] = \frac{1}{s(s-1)},\ E[d_2] = \frac{1}{s(s-2)},\ \cdots](/mediawiki/images/math/5/e/6/5e613b4f7121f53e4871199071824db9.png)
![\textstyle
E[d_i] = \frac{1}{s(s-i)},\ \cdots \ E[d_{s-1}] = \frac{1}{s}](/mediawiki/images/math/0/0/a/00a402eafc167511df568fe37fa755ca.png)
![\begin{align}
E[l_2] &= \textstyle l_1 + d_1 = \frac{1}{s^2} + \frac{1}{s(s-1)}\\
E[l_3] &= \textstyle l_1 + d_1 + d_2 = \frac{1}{s^2} + \frac{1}{s(s-1)} + \frac{1}{s(s-2)}\\
\cdots \\
E[l_i] &= \textstyle \frac{1}{s}\sum^{i-1}_{j=0}\frac{1}{s-j}\\
&= \textstyle \frac{1}{s} (\sum^{s}_{j=1}\frac{1}{j} - \sum^{s-i}_{j=1}\frac{1}{j})\\
&\simeq \textstyle \frac{1}{s} \log\frac{s}{s-i}
\end{align}](/mediawiki/images/math/2/e/7/2e70a96c6303c754affa0897cae8766f.png)
![\begin{align}
E[l_i] &= \textstyle\frac{1}{s}\sum^{s-i}_{j=0}\frac{1}{s-j}\\
&= \textstyle\frac{1}{s}(\sum^{s}_{j=1}\frac{1}{j} - \sum^{i-1}_{j=1}\frac{1}{j})\\
&\simeq \textstyle\frac{1}{s} \log\frac{s}{i-1}
\end{align}](/mediawiki/images/math/a/7/e/a7e27641cef60756c3f8e9fee40d09be.png)