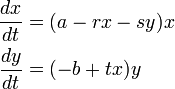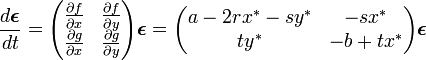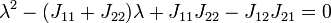Aritalab:Lecture/NetworkBiology/Stability
Contents |
系の安定性
一般的な 2 次元の系 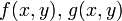 を考え、固定点 (= 時間依存しない解のこと。不動点とも呼ぶ) を
を考え、固定点 (= 時間依存しない解のこと。不動点とも呼ぶ) を 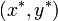 としましょう。
としましょう。
固定点に近い位置を 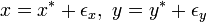 と書いて一次項まで近似すると
と書いて一次項まで近似すると
となります。関数 g についても同様です。これをヤコビ行列の形に書けば
です。ヤコビアンの簡単な場合として対角行列を考えましょう。
この解は以下のようになります。
x, y について書き直すと以下になります。
つまり 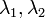 の値(それぞれ固定点における関数 f, g の微分値) が共に負であれば
の値(それぞれ固定点における関数 f, g の微分値) が共に負であれば 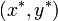 は誘引点、共に正であれば反発点、片方だけ負であれば鞍点 (saddle point) となります。
は誘引点、共に正であれば反発点、片方だけ負であれば鞍点 (saddle point) となります。
ヤコビアンが対角行列でない場合、行がヤコビアンの左固有ベクトルに対応する行列 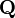 を用意し、
を用意し、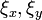 を定義します。
を定義します。
もし 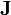 が固有値を持つならば
が固有値を持つならば 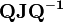 によって対角化することで
によって対角化することで 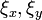 が互いに独立に時間発展することになります。
が互いに独立に時間発展することになります。
固有値が複素数になる場合 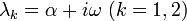 、一般解は指数的に増減する部分と振動する部分の積になります (C: 虚数, A, B: 実数)。
、一般解は指数的に増減する部分と振動する部分の積になります (C: 虚数, A, B: 実数)。
パラメータ α が負の場合は固定点に落ち込むスパイラル(安定点)になり、正の場合は固定点から遠ざかる不安定点です。一点に落ち込むことなく、安定した軌道を描く場合もあります。これをリミットサイクルと呼びます。
ロトカ・ヴォルテラ方程式
生態系の解析では、被食者 x と捕食者 y を扱うものが多くあります。以下の仮定を考えます。
- 被食者は一定割合 a で増加するが、個体数が多くなりすぎると餌不足で増加率が減少する。
- 捕食者は一定割合 b で死滅する。
以下の方程式を考えます。a, b, r, s, t は全て正のパラメータです。
固定点は 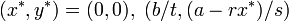 です。周辺の挙動をみてみます。
です。周辺の挙動をみてみます。
行列の固有方程式
を考え、固有値がともに負になるかを検討します。
固定点(0,0)の場合
ヤコビアンは
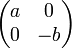 です。固有値の一方だけ負なので、これは鞍点です。
です。固有値の一方だけ負なので、これは鞍点です。
固定点 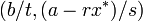 の場合
の場合
ヤコビアンは
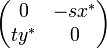 です。この場合の固有値は複素数となり、実数部分を持ちません。そのため、固定点に落ち込んでいくことのない(吸引的でない)安定点になります。
この方程式で r = 0 とおいた場合が、大変有名なロトカ・ヴォルテラ方程式です。
です。この場合の固有値は複素数となり、実数部分を持ちません。そのため、固定点に落ち込んでいくことのない(吸引的でない)安定点になります。
この方程式で r = 0 とおいた場合が、大変有名なロトカ・ヴォルテラ方程式です。
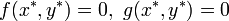
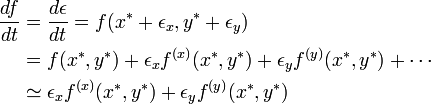

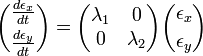
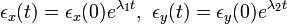
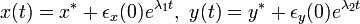
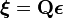
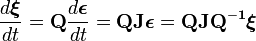
![\, \xi_k(t) = \mbox{Re}[ C e^{(\alpha+ i\omega)t}] = e^{\alpha t} (A \cos \omega t + B \sin \omega t)](/mediawiki/images/math/9/1/b/91b6a40d4a9d0a8c9c136296457fdcff.png)