Aritalab:Lecture/NetworkBiology/Random Walk/Recurrence
m |
m (→k = 1 の場合) |
||
| Line 153: | Line 153: | ||
原点から出発して、 ''n'' ステップ目ではじめて ''k'' = 1 になる確率 <math>g_1 (n)\,</math> を考えます。 | 原点から出発して、 ''n'' ステップ目ではじめて ''k'' = 1 になる確率 <math>g_1 (n)\,</math> を考えます。 | ||
| − | * ''n'' = 0 のとき、明らかに <math>g_1 (0) = 0\,</math> | + | * ''n'' = 0 のとき、明らかに <math>g_1 (0) = 0\,</math> |
| − | + | * ''n'' = 1 のとき、明らかに <math>g_1 (1) = p\,</math> | |
| − | * ''n'' = 1 のとき、明らかに <math>g_1 (1) = p\,</math> | + | |
* ''n'' > 1 のとき | * ''n'' > 1 のとき | ||
最初のステップは必ず左です。その後、 ''m'' - 1 回 ( ''m'' < ''n'' ) で右隣の原点に初めて戻り、さらに ''n'' - ''m'' 回で初めて位置 1 に到達します。その確率は <math> q g_1(m-1) g_1(n-m)\,</math> です。''m'' についての和を取ると | 最初のステップは必ず左です。その後、 ''m'' - 1 回 ( ''m'' < ''n'' ) で右隣の原点に初めて戻り、さらに ''n'' - ''m'' 回で初めて位置 1 に到達します。その確率は <math> q g_1(m-1) g_1(n-m)\,</math> です。''m'' についての和を取ると | ||
Revision as of 11:43, 4 July 2011
原点から出発したランダムウォークが原点に戻ってくる確率を再帰確率といいます。 ここでは一次元ランダムウォークを考えます。
Contents |
再帰確率と二項係数の関係
原点から出発して 2n ステップ後に再び原点に戻っている確率 f ( 2 n ) は、左右にちょうど n 回ずつ移動すればよいので
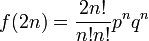
になります。f (0) = 1 です。これは原点に何回戻ってもよい確率なので、 2n ステップ後に初めて原点に戻ってくる再帰確率を g ( 2 n ) と書くと、
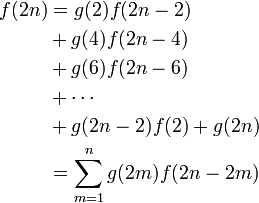
となります。この関係式から
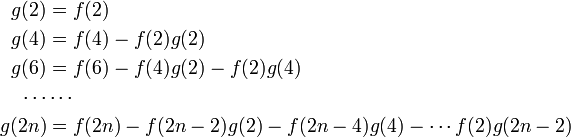
が求まり、二項係数 f ( 2 n ) を用いて g ( 2 n ) を書き下すことができます。
再帰確率の母関数
ここでは再帰確率を母関数を用いて求めてみます。 f, g の母関数を考えます。 g は 2 n 回目で初めて原点に戻ることを意味する関数なので n = 1 からスタートするところに注意しましょう。
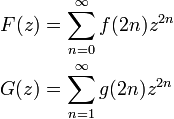
ここで f と g の関係式から
![\begin{align}
f(2n) &= \sum^n_{m=1} g(2m) f(2n - 2m)\\
f(2n) z^{2n} & = \sum^n_{m=1} g(2m) z^{2m} f(2n - 2m) z^{2n-2m} \\
\sum^{\infty}_{n=1} f(2n) z^{2n} & = \sum^{\infty}_{n=1}\Big[ \sum^n_{m=1} g(2m) z^{2m} f(2n - 2m) z^{2n-2m} \Big]\\
\end{align}](/mediawiki/images/math/1/5/5/155475c2462e65fe03e29aed19942d43.png)
さらに
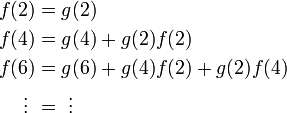
という関係を縦方向に眺めることによって、右辺の2重和の順序を入れ替えます。
![\begin{align}
\sum^{\infty}_{n=1} f(2n) z^{2n} &= \sum^{\infty}_{n=1}\Big[ \sum^n_{m=1} g(2m) z^{2m} f(2n - 2m) z^{2n-2m} \Big]\\
&= \sum^{\infty}_{m=1} g(2m)z^{2m} \sum^{\infty}_{n=m} f(2n - 2m) z^{2n-2m}\\
&= G(z) F(z)
\end{align}](/mediawiki/images/math/2/1/a/21ad8d1808112f68af1d469d0c711430.png)
左辺は 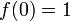 を含まないので
を含まないので 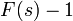 となり、
となり、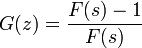 となります。
無限級数
となります。
無限級数 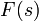 が発散するときは
が発散するときは 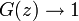 となって再帰確実であり(必ず原点にもどる)、有限な値に収束するときは
となって再帰確実であり(必ず原点にもどる)、有限な値に収束するときは 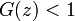 で再帰不確実です。
で再帰不確実です。
実は、二項係数の母関数 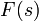 は閉じた式に書き下すことができます。(母関数のページを参照。)
は閉じた式に書き下すことができます。(母関数のページを参照。)
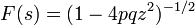
これから
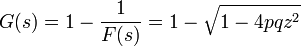
となり再帰確率は
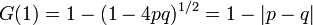
になります。
原点に戻ってくる回数
再帰確率を r としましょう。ランダムウォークが原点に戻ってこない確率は (1 − r) です。いったん原点に戻ってきたら、ランダムウォークを再出発させると考えると、ちょうど1回原点に戻ってくる確率は r (1 − r )、ちょうど2回原点に戻ってくる確率は r2 (1 − r )、ちょうど n 回原点に戻ってくる確率は rn (1 − r ) になります。戻ってくる回数の期待値は
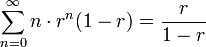
になります(この等式の導出は母関数のページを参照)。一方で、ランダムウォークが原点に戻ってくる回数は n ステップ後に原点にいる確率をすべて足し合わせたものにも等しいので
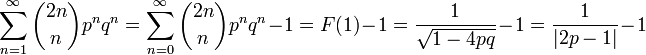
とも書けます(この等式の導出も母関数のページを参照)。
両方の値を等しいとすることで、たとえば p > 1/2 と仮定して
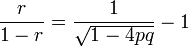
とおけば
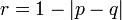
となり、母関数を用いた 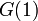 の値と一致します。
の値と一致します。
平均再帰時間
p = q = 1/2 のときだけ、再帰確実なので平均再帰時間を考えることができます。
![\sum^{\infty}_{n=0} 2n \cdot g(2n) = \Big[ \frac{d G(z)}{dz} \Big]_{z=1} =
[ z(1 - z^2)^{-1/2} ]_{z=1} = \infty](/mediawiki/images/math/c/d/1/cd1f15d03c51fb9d2ffcb3bcd6ce1e9f.png)
つまり、原点には必ず戻りますが無限時間かかる可能性があります。
到達確率
原点から出発して n ステップ後に位置 k に初めて到達する確率 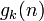 は、再帰確率と同様に求められます。ここでは一般性を失わずに k > 0 とし、 n と k の偶奇が一致する制約を無視して議論を進めます。まず n ステップ後に 位置 k にいる確率
は、再帰確率と同様に求められます。ここでは一般性を失わずに k > 0 とし、 n と k の偶奇が一致する制約を無視して議論を進めます。まず n ステップ後に 位置 k にいる確率 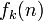 から求めます。
から求めます。
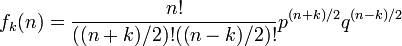
再帰確率の場合と同じく、n ステップ後に初めて k に到達する関数との関係を考えます。初めて k に到達したらそこを原点として残りのステップを関数 f で記述できるので以下のようになります。
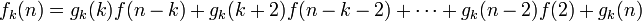
ここで
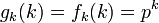
です。二項係数 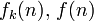 を用いて
を用いて 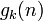 を書き下すことができます。
を書き下すことができます。
k = 1 の場合
原点から出発して、 n ステップ目ではじめて k = 1 になる確率 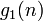 を考えます。
を考えます。
- n = 0 のとき、明らかに
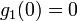
- n = 1 のとき、明らかに
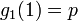
- n > 1 のとき
最初のステップは必ず左です。その後、 m - 1 回 ( m < n ) で右隣の原点に初めて戻り、さらに n - m 回で初めて位置 1 に到達します。その確率は 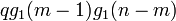 です。m についての和を取ると
です。m についての和を取ると
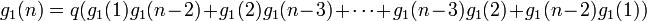
これを n = 2 から並べましょう。
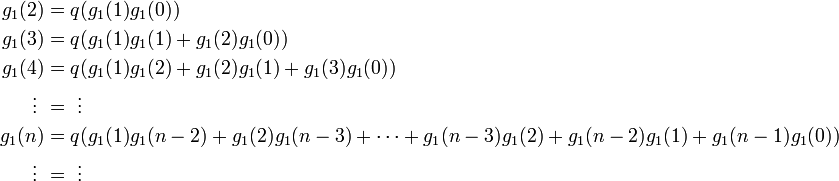
母関数 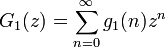 を考慮しながら縦方向に足し合わせます。
を考慮しながら縦方向に足し合わせます。
![\begin{align}
\sum^{\infty}_{n=2} g_1(n)z^n &= q \sum^{\infty}_{n=2} \sum^{n-1}_{m=1} g_1(m)g_1(n-m-1) z^n\\
G_1(z) - pz &= q z \sum^{\infty}_{m=1}g_1(m) z^m \big[ \sum^{\infty}_{n=m+1} g_1(n-m-1) z^{n-m-1}\big]\\
G_1(z) - pz &= q z G_1(z)^2 \\
\end{align}](/mediawiki/images/math/2/7/6/27687b72121b4ec02ef3e06fd028130e.png)
この二次式を解くと ![G_1(z) = \frac{1}{2qz}[1 - (1 - 4 pqz^2)^{1/2}]](/mediawiki/images/math/8/3/b/83b2b6601328c585d5b92447dc5aff25.png) となります。(もう一つの解はz = 0 で発散する。)すなわち
となります。(もう一つの解はz = 0 で発散する。)すなわち
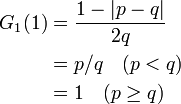
もし p < q (左のほうに行く確率が高い)なら、永遠に待っていても 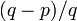 の確率で k = 1 に来ることはなく、p ≥ q の場合は必ず k = 1 に到達します。
の確率で k = 1 に来ることはなく、p ≥ q の場合は必ず k = 1 に到達します。
- 平均到達時間
![\sum^{\infty}_{n=0} n g_1(n) = \big[ \frac{d G_1(z)}{dz} \big]_{z=1}](/mediawiki/images/math/0/2/4/02497de47cd886bd03a04fa745b0a21f.png)