Aritalab:Lecture/NetworkBiology/Percolation on Graph

ランダムグラフでのパーコレーション

ランダムグラフは、ある次数分布に従うツリーとみなすことができる。 これを扱うには、母関数という概念を利用する。

次数分布の母関数

一般の次数分布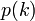$p(k)$の母関数は上で述べた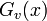$G_v(x)$になる。ある頂点vの隣にある頂点wの次数分布はもはや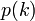$p(k)$ではなく、母関数も異なる。辺をランダムに1本選んだとき、もう片方にある端点がどんな次数になっているかをあらわす分布が必要である。辺をランダムに選んだ先には、次数が大きい点が存在する確率が高い。つまり、もう片側にある端点の次数が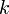$k$になる確率は、辺の数で重みをつけた次数分布に比例して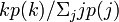$\textstyle kp(k)/\Sigma_j jp(j)$となる（分母は正規化定数）。よってある頂点vの隣にある頂点wの次数分布の母関数は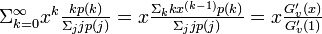$\textstyle \Sigma_{k=0}^{\infty}x^k\frac{kp(k)}{\Sigma_jjp(j)} = x\frac{\Sigma_k kx^{(k-1)}p(k)}{\Sigma_jjp(j)} = x\frac{G'_v(x)}{G'_v(1)}$となる。

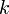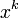母関数においては、次数$k$に対して$x^k$が対応することに注意しよう。頂点vの先にwがついているとき、wが持つ辺の一つはvに戻るため、外側に伸びる辺は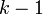$k-1$になる。そのときの母関数は上の式を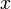$x$で割ればよく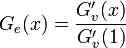$G_e(x) = \frac{G'_v(x)}{G'_v(1)}$と書ける。

相転移が起きるのは頂点から伸びていく辺の期待値が1をちょうど超えるとき、つまり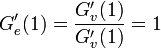$G_e'(1) = \frac{G'_v(1)}{G'_v(1)} = 1$のとき。すなわち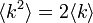$\langle k^2 \rangle = 2 \langle k \rangle$のときになる。別の書き方では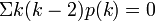$\Sigma k(k-2)p(k) = 0$だが、この和のうち負の値になるのは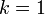$k=1$のときだけ、つまり行き止まりが極端に多くない限り、連結成分は繋がって無限に大きくなることを意味している。

パーコレーション

パーコレーションにおいては、確率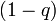$(1-q)$で辺が繋がらなくなる。実効的な次数が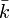$\bar{k}$になる確率は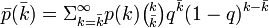$\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}$である。

大雑把に言うと相転移を起こすのは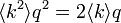$\langle k^2 \rangle q^2= 2 \langle k \rangle q$のとき、つまり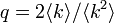$q = 2 \langle k \rangle / \langle k^2 \rangle$のあたりである。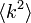$\langle k^2 \rangle$が大きいと非常に低いパーコレーション確率でも相転移が起こる。つまり感染率が低くてもネットワーク全体に蔓延する。この値はべき分布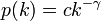$p(k)=ck^{-\gamma}$のときおよそ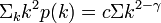$\Sigma_kk^2p(k) = c\Sigma k^{2-\gamma}$になるため、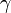$\gamma$が3以下であればパーコレートする。