Aritalab:Lecture/NetworkBiology/Percolation on Graph
m |
|||
| Line 1: | Line 1: | ||
| − | == | + | ==グラフ上のパーコレーション== |
| − | + | ||
| − | + | ||
| − | + | ||
| + | グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみよう。 | ||
| + | ここでは母関数という概念を利用する。 | ||
==次数分布の母関数== | ==次数分布の母関数== | ||
| − | + | グラフの次数分布<math>p(k)</math>を与えられたとき、その母関数は | |
| − | + | <math>G_v(z) = \sum p(k) z^k</math> | |
| + | しかし、頂点''v''の隣にある頂点''w''の次数分布はもはや<math>p(k)</math>ではない。 | ||
| + | 辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えよう。 | ||
| + | 選ばれた辺の先には、他の点が等確率でくることはない。次数の大きい点のほうが、次数に比例して存在する確率が高くなるだろう。 | ||
| + | つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した<math>\textstyle kp(k)/\Sigma_j jp(j)</math>となる(分母は正規化定数)。 | ||
| + | よってある頂点''v''の隣にある頂点''w''の次数分布の母関数は | ||
| − | + | <math>\sum_{k=0}^{\infty}x^k\frac{kp(k)}{\Sigma_jjp(j)} = x\frac{\Sigma_k kx^{(k-1)}p(k)}{\Sigma_jjp(j)} = x\frac{G'_v(x)}{G'_v(1)}</math> | |
| + | |||
| + | 母関数においては、次数<math>k</math>に対して<math>x^k</math>が対応する。 | ||
| + | 頂点''v''の先に''w''がついているとき、''w''から''v''以外に伸びる辺数に注目しよう。 | ||
| + | その母関数は上の式を<math>x</math>で割ればよいから | ||
| + | |||
| + | <math>G_w(x) = \frac{G'_v(x)}{G'_v(1)}</math> | ||
| + | |||
| + | ==占有される頂点の母関数== | ||
| + | |||
| + | パーコレーションで相転移が起きるのは、頂点から伸びていく辺の期待値が1をちょうど超えるときである。 | ||
| + | ただし、このときの母関数はグラフ全体の次数分布を示す<math>G_v</math>ではなく、占有された頂点のみによる部分ネットワークの母関数である。 | ||
| + | したがって、母関数を区別して<math>F_v</math>と記そう。''F''と''G''の関係は、各頂点が確率''q''で占有されるため | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | F'_v(v) &= q G'_v(v) = q \langle k \rangle \\ | ||
| + | F''_v(v) &= q^2G''_v(v) = q^2 (\langle k^2 \rangle - \langle k \rangle) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | つまり''G''と''F''の次数平均と二乗平均をそれぞれ<math>\langle k \rangle</math>, <math>\langle l \rangle</math>と書くと | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | \langle l \rangle &= q \langle k \rangle \\ | ||
| + | \langle l^2 \rangle &= q^2 (\langle k^2 \rangle - \langle k \rangle) + q \langle k \rangle | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | 相転移が起きるのは<math>F_w'(1) = 1</math>のときだから | ||
| + | |||
| + | <math> | ||
| + | F'_w(1) = \frac{F''_v(1)}{F'_v(1)} = 1 | ||
| + | </math> | ||
| + | |||
| + | に代入して | ||
| + | |||
| + | <math> | ||
| + | q_c = \frac{1}{\frac{\langle k^2 \rangle}{\langle k \rangle} - 1} | ||
| + | </math> | ||
| + | |||
| + | ==パーコレーション== | ||
| + | |||
| + | いかなる次数分布でも、<math>\langle k^2 \rangle</math>が<math>\langle k \rangle</math>に比して大きいと、低いパーコレーション確率で相転移が起こる。 | ||
| + | |||
| + | ===ランダムグラフの場合=== | ||
| + | |||
| + | ランダムグラフの場合は次数分布がポアソン分布になる。このとき<math>\langle k^2 \rangle = \langle k \rangle^2 + \langle k \rangle </math>になるので | ||
| + | |||
| + | <math>q_c = 1 / \langle k \rangle</math> | ||
| + | |||
| + | すなわち、平均次数が大きくなるほどパーコレートしやすくなる。 | ||
| + | |||
| + | ===スケールフリーネットワークの場合=== | ||
| + | |||
| + | べき分布<math>p(k)=ck^{-\gamma}</math>のとき | ||
| + | |||
| + | <math> | ||
| + | \langle k^2 \rangle = \Sigma_kk^2p(k) = c\Sigma k^{2-\gamma} | ||
| + | </math> | ||
| + | |||
| + | この値は<math>\gamma \leq 3</math>のときに発散する。有限のネットワークではその値も有限だが、大きな値になるために | ||
| + | 非常に低い値でパーコレートする。 | ||
<!---- | <!---- | ||
| + | |||
| + | 別の書き方では<math>\Sigma k(k-2)p(k) = 0</math>だが、この和のうち負の値になるのは<math>k=1</math>のときだけ、つまり行き止まりが極端に多くない限り、連結成分は繋がって無限に大きくなることを意味している。 | ||
| + | |||
==連結成分のサイズの母関数== | ==連結成分のサイズの母関数== | ||
ランダムに選んだ辺から出発したときの連結成分のサイズの分布を<math>H_e(x)</math>、ランダムに選んだ頂点を含む連結成分のサイズの分布を<math>H_v(x)</math>と書こう。辺を選んだとき、連結成分が先に広がるかどうかはもう片側にある端点の次数に依存し、その分布は<math>\textstyle kp(k)/\Sigma_j jp(j)</math>である。それぞれの先からも辺が伸びていくため | ランダムに選んだ辺から出発したときの連結成分のサイズの分布を<math>H_e(x)</math>、ランダムに選んだ頂点を含む連結成分のサイズの分布を<math>H_v(x)</math>と書こう。辺を選んだとき、連結成分が先に広がるかどうかはもう片側にある端点の次数に依存し、その分布は<math>\textstyle kp(k)/\Sigma_j jp(j)</math>である。それぞれの先からも辺が伸びていくため | ||
| Line 19: | Line 89: | ||
連結成分のサイズの期待値は<math>H_v'(1) = G_v(H_e(1)) + G_v'(1)H_e'(1)=</math> | 連結成分のサイズの期待値は<math>H_v'(1) = G_v(H_e(1)) + G_v'(1)H_e'(1)=</math> | ||
| − | |||
| − | + | ||
パーコレーションにおいては、確率<math>(1-q)</math>で辺が繋がらなくなる。実効的な次数が<math>\bar{k}</math>になる確率は<math>\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}</math>である。 | パーコレーションにおいては、確率<math>(1-q)</math>で辺が繋がらなくなる。実効的な次数が<math>\bar{k}</math>になる確率は<math>\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}</math>である。 | ||
<!---- | <!---- | ||
このとき<math>\langle \bar{k} \rangle = \langle k \rangle q</math>、<math>\langle \bar{k^2} \rangle = \langle k^2 \rangle + \langle k \rangle q (1-q)</math>になる。 | このとき<math>\langle \bar{k} \rangle = \langle k \rangle q</math>、<math>\langle \bar{k^2} \rangle = \langle k^2 \rangle + \langle k \rangle q (1-q)</math>になる。 | ||
| − | |||
| − | 大雑把に言うと相転移を起こすのは<math>\langle k^2 \rangle q^2= 2 \langle k \rangle q</math>のとき、つまり<math>q = 2 \langle k \rangle / \langle k^2 \rangle</math>のあたりである。 | + | |
| + | 大雑把に言うと相転移を起こすのは<math>\langle k^2 \rangle q^2= 2 \langle k \rangle q</math>のとき、つまり<math>q = 2 \langle k \rangle / \langle k^2 \rangle</math>のあたりである。 | ||
| + | |||
| + | つまり感染率が低くてもネットワーク全体に蔓延する。 | ||
| + | ---> | ||
Revision as of 10:10, 3 June 2010
Contents |
グラフ上のパーコレーション
グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみよう。 ここでは母関数という概念を利用する。
次数分布の母関数
グラフの次数分布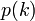 を与えられたとき、その母関数は
を与えられたとき、その母関数は
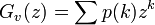
しかし、頂点vの隣にある頂点wの次数分布はもはや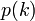 ではない。
辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えよう。
選ばれた辺の先には、他の点が等確率でくることはない。次数の大きい点のほうが、次数に比例して存在する確率が高くなるだろう。
つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した
ではない。
辺をランダムに1本選んだとき、もう片方にある端点がどんな次数分布をとるか考えよう。
選ばれた辺の先には、他の点が等確率でくることはない。次数の大きい点のほうが、次数に比例して存在する確率が高くなるだろう。
つまり、もう片側にある端点の次数分布は、最初の次数分布に辺の数で重みをつけてから正規化した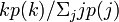 となる(分母は正規化定数)。
よってある頂点vの隣にある頂点wの次数分布の母関数は
となる(分母は正規化定数)。
よってある頂点vの隣にある頂点wの次数分布の母関数は
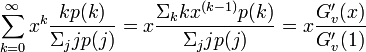
母関数においては、次数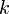 に対して
に対して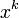 が対応する。
頂点vの先にwがついているとき、wからv以外に伸びる辺数に注目しよう。
その母関数は上の式を
が対応する。
頂点vの先にwがついているとき、wからv以外に伸びる辺数に注目しよう。
その母関数は上の式を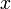 で割ればよいから
で割ればよいから
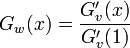
占有される頂点の母関数
パーコレーションで相転移が起きるのは、頂点から伸びていく辺の期待値が1をちょうど超えるときである。
ただし、このときの母関数はグラフ全体の次数分布を示す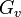 ではなく、占有された頂点のみによる部分ネットワークの母関数である。
したがって、母関数を区別して
ではなく、占有された頂点のみによる部分ネットワークの母関数である。
したがって、母関数を区別して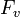 と記そう。FとGの関係は、各頂点が確率qで占有されるため
と記そう。FとGの関係は、各頂点が確率qで占有されるため
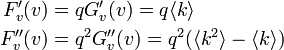
つまりGとFの次数平均と二乗平均をそれぞれ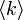 ,
, 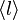 と書くと
と書くと
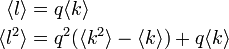
相転移が起きるのは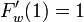 のときだから
のときだから
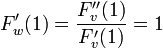
に代入して
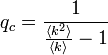
パーコレーション
いかなる次数分布でも、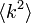 が
が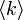 に比して大きいと、低いパーコレーション確率で相転移が起こる。
に比して大きいと、低いパーコレーション確率で相転移が起こる。
ランダムグラフの場合
ランダムグラフの場合は次数分布がポアソン分布になる。このとき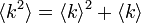 になるので
になるので
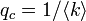
すなわち、平均次数が大きくなるほどパーコレートしやすくなる。
スケールフリーネットワークの場合
べき分布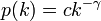 のとき
のとき
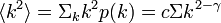
この値はFailed to parse (lexing error): \gamma \leq 3 のときに発散する。有限のネットワークではその値も有限だが、大きな値になるために 非常に低い値でパーコレートする。