Aritalab:Lecture/NetworkBiology/Markov Chains/Queue
From Metabolomics.JP
待ち行列
窓口に並ぶ客の人数 i をモデルしよう。 単位時間において以下の事象が発生する。
- もし i < n だったら、確率 α で客が一人増える。
- もし i > 0 なら、確率 β で先頭から順に客は減る。
- それ以外の場合、客の数は変化しない。
時刻 t における行列の長さを考えると、有限のマルコフ連鎖になっている。遷移確率は以下のようになる。
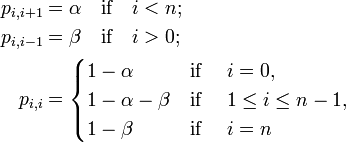
マルコフ連鎖は既約、有限、非周期的なので唯一の定常分布 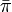 を持つ。
満たすべき式は
を持つ。
満たすべき式は
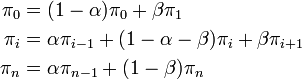
これを解くと 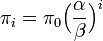 。
更に
。
更に 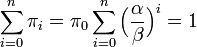 より
より
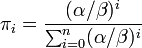
- 結論
- α > β のときは行列が長い確率の方が大きい
- α = β のとき、行列の長さは0からnまで等確率
同じ結果は、定常状態において α πi = β πi +1 という考察からも導くことができる。πi = (α/β) πi +1 から帰納法で πi = π0(α/β)i となる。
列の長さに上限 n が無い場合、マルコフ連鎖は有限ではない。もし定常分布があるとしたら(ない可能性もある)
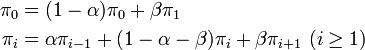
の解が存在しなくてはならない。前出の解から類推して
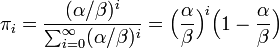
が答えになる。このとき α < β でないと定常分布は存在しない。