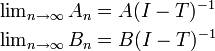Aritalab:Lecture/NetworkBiology/Markov Chains/Genetics

Inbreeding

遺伝子の優性アレル A と劣性アレル a の交配パターンをモデルしましょう。アレルを A, a で表すと、遺伝型は AA, Aa, aa の 3 通り、交配パターンは AA × AA, AA × Aa, Aa × Aa, AA × aa, Aa × aa, aa × aa の 6 通りあります。親子のアレルパターンを行列であらわすと以下のようになります。

• 親が AA × AA の場合、子供は必ず AA なので、子供どうしのかけ合わせも AA × AA
• 親が AA × Aa の場合、子供は確率 1/2, 1/2 で AA, Aa なので、子供のかけ合わせは AA × AA, AA × Aa, Aa × Aa
• 親が Aa × Aa の場合、子供は確率 1/4, 1/2, 1/4 で AA, Aa, aa なので、子供のかけ合わせは全パターンが生じる
• 親が Aa × aa の場合、子供は確率 1/2 で Aa, aa なので、子供のかけ合わせは Aa × Aa, Aa × aa, aa × aa
• 親が AA × aa の場合、子供は必ず Aa なので、子供どうしのかけ合わせは Aa × Aa
• 親が aa × aa の場合、子供は必ず aa なので、子供どうしのかけ合わせも aa × aa

確率行列 P	children
parents ↓	AA × AA	AA × Aa	Aa × Aa	Aa × aa	AA × aa	aa × aa
AA × AA	1	0	0	0	0	0
AA × Aa	1/4	1/2	1/4	0	0	0
Aa × Aa	1/16	1/4	1/4	1/4	1/8	1/16
Aa × aa	0	0	1/4	1/2	0	1/4
AA × aa	0	0	1	0	0	0
aa × aa	0	0	0	0	0	1

= $\begin{bmatrix} 1 && \mathbf{0} && 0 \\ \mathbf{A} && \mathbf{T} && \mathbf{B} \\ 0 && \mathbf{0} && 1 \end{bmatrix}$

ここで ${\mathbf T} = \begin{bmatrix} 1/2 && 1/4 && 0 && 0\\ 1/4 && 1/4 && 1/4 && 1/8\\ 0 && 1/4 && 1/2 && 0\\ 0 && 1 && 0 && 0 \end{bmatrix}$

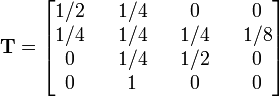
これは 6 状態のマルコフ連鎖で、AA × AA と aa × aa が吸収状態になっています。真ん中の赤で示した 4 × 4 行列（ T と書きましょう）は過渡的状態で、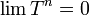$\lim T^n = 0$ です。この行列 T に対して n 乗を計算すれば、n 世代後における遺伝型の分布を求められます。

${\mathbf P}^2 = \begin{bmatrix} 1 && \mathbf{0} && 0 \\ \mathbf{(I+T)A} && \mathbf{T}^2 && \mathbf{(I+T)B} \\ 0 && \mathbf{0} && 1 \end{bmatrix}$

${\mathbf P}^3 = \begin{bmatrix} 1 && \mathbf{0} && 0 \\ \mathbf{(I+T + T^2)A} && \mathbf{T}^3 && \mathbf{(I+T + T^3)B} \\ 0 && \mathbf{0} && 1 \end{bmatrix}$

：

${\mathbf P}^n = \begin{bmatrix} 1 && \mathbf{0} && 0 \\ \mathbf{A}_n && \mathbf{T}^n && \mathbf{B}_n \\ 0 && \mathbf{0} && 1 \end{bmatrix}$

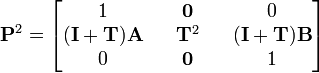
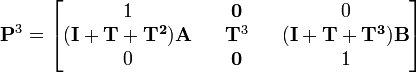
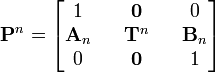
ここで行列の級数 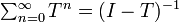$\textstyle\sum^{\infty}_{n=0}T^n = (I - T)^{-1}$ を利用すれば

$\begin{align} \textstyle\lim_{n\rightarrow \infty}A_n &= A(I-T)^{-1}\\ \textstyle\lim_{n\rightarrow \infty}B_n &= B(I-T)^{-1} \end{align}$