Aritalab:Lecture/NetworkBiology/Markov Chains
Contents |
マルコフ連鎖
グラフ上のランダムウォークを考えよう。
離散確率過程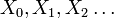 は
は
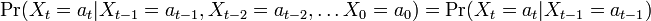
を満たすときにマルコフ連鎖 (Markov chain) と呼ばれる。状態  が状態
が状態  のみに依存して決まる性質をマルコフ性 (Markov property) または無記憶性 (memoryless property) という。
のみに依存して決まる性質をマルコフ性 (Markov property) または無記憶性 (memoryless property) という。
マルコフ連鎖において状態 i から j への遷移確率を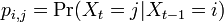 と書けば、マルコフ連鎖は遷移行列
と書けば、マルコフ連鎖は遷移行列
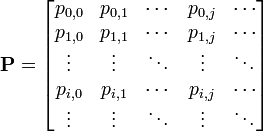
で記述できる。記法を拡張し、i から j へ正確に m ステップで移る遷移確率を
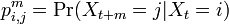
と書こう。1ステップ目で移動した先を k と書くと
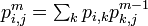 であるから、遷移行列
であるから、遷移行列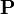 を m 乗すれば正確に m ステップで移った先を示す遷移行列を得る(数学的帰納法)。
を m 乗すれば正確に m ステップで移った先を示す遷移行列を得る(数学的帰納法)。
既約
状態 i から j へ何ステップかで到達できる場合、j は i から到達可能 (accessible) と呼ぶ。
互いに到達可能な状態 i, j どうしを連結 (communicate) しているといい、 と書く。連結性は同値類を形成する。
と書く。連結性は同値類を形成する。
- 反射律: いかなる状態 i も、
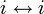
- 対称律:
 なら
なら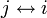
- 推移律:
 かつ
かつ なら
なら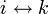
全ての状態が同じ同値類に属すとき、つまり全ての頂点が互いに連結なとき、マルコフ連鎖は既約 (irreducible) という。既約なマルコフ連鎖をグラフ表現すると強連結 (strongly connected) になっていて、任意の頂点から任意の頂点に移動できる。
再帰性
状態 i から出発し時刻 t になって初めて j に到達する確率を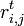 と書く。
前出の
と書く。
前出の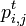 は複数回jを訪れることを許すため、
は複数回jを訪れることを許すため、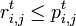 となることに注意しよう。
となることに注意しよう。
状態 i を
-
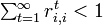 であれば一時的 (transient)
であれば一時的 (transient)
-
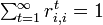 であれば再帰的 (recurrent)
であれば再帰的 (recurrent)
と呼ぶ。全ての状態が再帰的であれば、マルコフ連鎖自体を再帰的と呼ぶ。
状態 i が再帰的であっても、再帰までのステップ数(再帰時間)の期待値 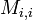 が有限とは限らない。
例えば正の整数値に対応するマルコフ連鎖を仮定し、状態 i から確率
が有限とは限らない。
例えば正の整数値に対応するマルコフ連鎖を仮定し、状態 i から確率 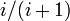 で状態 i+1 に、確率
で状態 i+1 に、確率 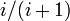 で状態1に移動する系を考えよう。
状態1からスタートして最初の t ステップで1に戻らない確率は
で状態1に移動する系を考えよう。
状態1からスタートして最初の t ステップで1に戻らない確率は
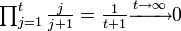
したがって状態1は再帰的で、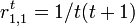 。
しかし初めて状態1に戻ってくるまでのステップ数の期待値は
。
しかし初めて状態1に戻ってくるまでのステップ数の期待値は
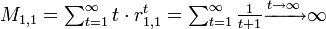
再帰時間の期待値が有限な状態を正再帰的 (positive recurrent)、そうでない場合を零再帰的 (null recurrent) とよぶ。 零再帰性を満たすには無限の状態数が必要になる。 状態数が N 個で有限の場合、少なくとも N+1 ステップ目に既に訪れた状態に辿り着く。 よって少なくとも一つの再帰的な状態が存在する。
周期性
状態 i に戻ってくるまでのステップ数が k >1 の倍数回に限られ、しかも k がこの性質を持つ最大値の場合、状態 i は周期 k であるという。 k=1 であれば状態は非周期的であるという。 全ての状態が非周期的で正再帰的なマルコフ連鎖はエルゴード的 (ergodic) であるという。
定常分布
マルコフ連鎖の遷移行列 に対して
に対して
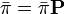
を満たし、要素の総和が1、つまり 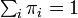 となるような行ベクトル
となるような行ベクトル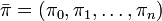 を定常分布 (stationary distribution) という。
有限で既約、エルゴード的なマルコフ連鎖は、唯一つの定常分布
を定常分布 (stationary distribution) という。
有限で既約、エルゴード的なマルコフ連鎖は、唯一つの定常分布 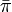 を持ち、 再帰時間の期待値との間に
を持ち、 再帰時間の期待値との間に
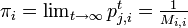
が成り立つ。
これは再帰時間の期待値が出発する状態 j に依存しないことを意味し、再帰までのステップ数期待値が 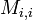 ならば状態 i に戻ってくる確率が
ならば状態 i に戻ってくる確率が 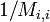 であることに対応する。つまり
であることに対応する。つまり
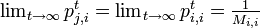
さらに定常分布においては、各状態に入る確率と出る確率は等しいことにも注意する。全ての状態 i, j に対し
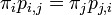
仮に定常分布が二つあるとして、もう一つの分布を 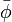 と書く。
定常分布であるから
と書く。
定常分布であるから
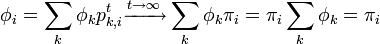
すなわち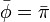 となる。
となる。
具体例
待ち行列
窓口に並ぶ客の人数 i をモデルしよう。 単位時間において以下の事象が発生する。
- もし i < n だったら、確率
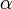 で客が一人増える。
で客が一人増える。
- もし i > 0なら、確率
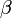 で先頭から順に客は減る。
で先頭から順に客は減る。
- それ以外の場合、客の数は変化しない。
時刻 t における行列の長さを 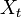 であらわす。すると以下の遷移確率を持つマルコフ連鎖で記述できる。
であらわす。すると以下の遷移確率を持つマルコフ連鎖で記述できる。
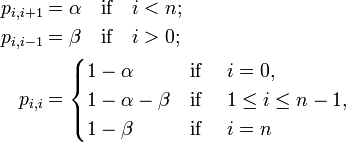
マルコフ連鎖は既約、有限、非周期的なので唯一の定常分布 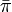 を持つ。
満たすべき式は
を持つ。
満たすべき式は
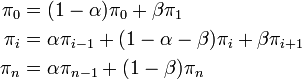
これを解くと 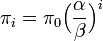 。
更に
。
更に 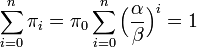 より
より
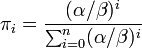
出生死亡過程
モラン過程
個体数を n とし、状態 i から i+1, i-1 の状態へそれぞれ確率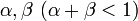 で遷移する場合を考える。
また状態 0 と n は吸収状態とする。(従って定常分布は存在しない。)
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。
で遷移する場合を考える。
また状態 0 と n は吸収状態とする。(従って定常分布は存在しない。)
このマルコフ連鎖を1958年にモデルを発表した遺伝学者PAP MoranにちなんでMoran過程という。
状態 i から出発して状態 n に到達する確率を 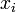 と書く。
と書く。
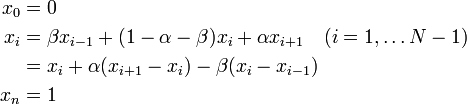
ここで記法
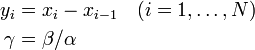
を導入すると

を得る。
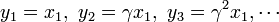
を足し合わせると
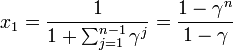
これと
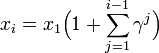
をあわせて
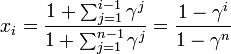
n 個体の集団において、全ての個体が最初タイプAであるとする。
タイプBという突然変異が 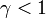 を満たす、すなわちAよりも優位で個体数を増やす傾向にあるとする。
を満たす、すなわちAよりも優位で個体数を増やす傾向にあるとする。
このとき1個生じたタイプBが集団 n の中に固定される(集団全体をカバーする)確率は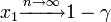 。
いかに優位な変異でも、必ず固定される訳ではない点に注意する。
。
いかに優位な変異でも、必ず固定される訳ではない点に注意する。
木村の中立進化説
突然変異が完全に中立な場合、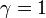 から
から 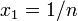 。
確率 m でタイプBという突然変異が生じるとき、Bの生まれる個数は mn になるから、最初のBが生まれるまでの平均時間は
。
確率 m でタイプBという突然変異が生じるとき、Bの生まれる個数は mn になるから、最初のBが生まれるまでの平均時間は 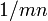 である。
である。
結局、全てタイプAの集団が、全てタイプBの集団に進化する速度は、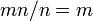 となり、集団のサイズに依存しない。ここから「分子時計」仮説が導かれる。
となり、集団のサイズに依存しない。ここから「分子時計」仮説が導かれる。