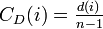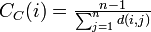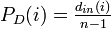Aritalab:Lecture/NetworkBiology/Link Analysis
| Line 1: | Line 1: | ||
| − | + | =歴史= | |
* 1998 Jan: J. KleinbergがHITSアルゴリズムを発表(9th ACM-SIAM DA) | * 1998 Jan: J. KleinbergがHITSアルゴリズムを発表(9th ACM-SIAM DA) | ||
* 1998 Apr: S. Brin, L. PageがPageRankを発表(7th WWW) | * 1998 Apr: S. Brin, L. PageがPageRankを発表(7th WWW) | ||
| − | + | =Centrality= | |
| − | 無向グラフにおいて、頂点のネットワーク中心への近さを示す尺度を中心度(centrality)という。いずれの値も0- | + | 無向グラフにおいて、頂点のネットワーク中心への近さを示す尺度を中心度(centrality)という。いずれの値も0-1の間をとるようにスケーリングする。有向グラフには次に述べるprestigeを使った方がよい。 |
* Degree centrality ... 辺数が多い点を中心と考える。 | * Degree centrality ... 辺数が多い点を中心と考える。 | ||
| + | :: <math>\textstyle C_D(i)=\frac{d(i)}{n-1}</math> | ||
* Closeness centrality ... 全頂点への平均最短距離が短い点を中心と考える。 | * Closeness centrality ... 全頂点への平均最短距離が短い点を中心と考える。 | ||
| + | :: <math>\textstyle C_C(i)=\frac{n-1}{\sum^n_{j=1}d(i,j)}</math> | ||
* Betweenness centrality ... 全頂点間の最短経路に多く使われる点を中心と考える。同じ値で辺のbetweennessも定義できる。 | * Betweenness centrality ... 全頂点間の最短経路に多く使われる点を中心と考える。同じ値で辺のbetweennessも定義できる。 | ||
| + | :: <math>\textstyle C_B(i)=\sum_{j<k, j\neq i, k\neq i}\frac{p_{jk}(i)}{p_{jk}} \times N_{paths}^{-1}</math> ただし<math>N_{path}</math>は<math>i</math>を除いたネットワーク中の最短経路<math>p</math>の本数で<math>(n-1)(n-2)/2</math>。 | ||
| − | + | =Prestige= | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
有向グラフにおいて頂点の傑出具合を測る尺度を傑出度(prestige)という。 | 有向グラフにおいて頂点の傑出具合を測る尺度を傑出度(prestige)という。 | ||
* Degree prestige ... 多くの入力辺がある点を傑出していると考える。 | * Degree prestige ... 多くの入力辺がある点を傑出していると考える。 | ||
| + | :: <math>\textstyle P_D(i)=\frac{d_{in}(i)}{n-1}</math> | ||
* Proximity prestige ... より多くの頂点から到達できる点を傑出していると考える。Degree prestigeの拡張になっている。 | * Proximity prestige ... より多くの頂点から到達できる点を傑出していると考える。Degree prestigeの拡張になっている。 | ||
| + | :: <math>\textstyle P_P(i)=\frac{|I_i|/(n-1)}{\sum_{j\in I_i}d(j,i)/|I_i|}</math> ただし><math>I_i</math>は<math>i</math>より到達できる頂点集合。 | ||
* Rank prestige ... 高いランクの頂点に指されている頂点もランクが高いと考える。 | * Rank prestige ... 高いランクの頂点に指されている頂点もランクが高いと考える。 | ||
| + | :: <big>'''P<sub>R</sub>=A<sup>T</sup>P<sub>R</sub>'''</big> ただし'''P<sub>R</sub>'''は長さ<math>n</math>の縦ベクトル、'''A'''は隣接行列。つまり'''P<sub>R</sub>'''は'''A'''の固有値にあたる。 | ||
| − | + | =PageRank= | |
| − | + | Rank prestigeにおいて'''A'''を単なる隣接行列ではなく各頂点の次数(degree)で行方向にスケーリングした値、すなわち<math>\textstyle A_{ij}=\frac{1}{deg(i)}</math>としたものをPageRankと呼ぶ。 | |
| − | + | つまり、行列'''A'''を、ウェブページを訪れるユーザがページ内のリンクを等確率でクリックして次ページに移動するマルコフ過程の遷移行列と考え、PageRankはその定常分布に相当する。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
しかしこのままでは実用上以下の問題点がある。 | しかしこのままでは実用上以下の問題点がある。 | ||
| − | # マルコフ過程の定常分布は、全ての状態が再帰的 ( | + | # マルコフ過程の定常分布は、全ての状態が再帰的(recurrent)、つまり有限のステップで同じ状態に戻ってくることが可能でないと求まらない。つまり、どのページからも外に出るリンクがないとランクを付与できないページが生じる。 |
# ページ間のネットワークが強連結(strongly connected)でないと定常分布における確率が0となる頂点が生じてしまう。 | # ページ間のネットワークが強連結(strongly connected)でないと定常分布における確率が0となる頂点が生じてしまう。 | ||
# 遷移過程に周期性が存在すると、定常分布として収束しない。 | # 遷移過程に周期性が存在すると、定常分布として収束しない。 | ||
| − | + | これらの問題点を回避するため、ユーザはリンク先の無いページからは他の全ページに等確率で移動し、リンク先を持つページからも一定確率でランダムに他ページに移動すると仮定する。つまり | |
| − | <math>\mathbf{P}=\left( (1-\alpha)\frac{\mathbf{E}}{n}+\alpha\mathbf{A}^T\right) \mathbf{P}</math> | + | <math>\textstyle \mathbf{P}=\left( (1-\alpha)\frac{\mathbf{E}}{n}+\alpha\mathbf{A}^T\right) \mathbf{P}</math> |
| − | ここで行列 | + | ここで行列'''E'''は要素が全て1の正方行列。またパラメータαをdamping factorと呼び、<math>d=0.85</math>程度が用いられる。 |
===利点と欠点=== | ===利点と欠点=== | ||
| Line 74: | Line 39: | ||
ただ、問い合わせの内容を一切考慮しないのは欠点ともいえる。 | ただ、問い合わせの内容を一切考慮しないのは欠点ともいえる。 | ||
| − | + | =HITS= | |
| − | Hypertext Induced Topic | + | Hypertext Induced Topic Search(HITS)はオーソリティおよびハブと呼ばれる二種の頂点集合からなる二部グラフを求めるアルゴリズム。 |
オーソリティとは入力辺を多く持つページで多くのハブからリンクされる。 | オーソリティとは入力辺を多く持つページで多くのハブからリンクされる。 | ||
ハブとは出力辺を多く持つページで多くのオーソリティへリンクする。 | ハブとは出力辺を多く持つページで多くのオーソリティへリンクする。 | ||
| − | + | 各頂点におけるオーソリティとハブの次数をあらわす縦ベクトルはそれぞれ'''a = L<sup>T</sup>h, h = La''' | |
| − | + | とあらわされる。つまり | |
| − | + | '''a = L<sup>T</sup>La, h = LL<sup>T</sup>h''' | |
| − | + | となる。つまり'''a'''と'''h'''はそれぞれ'''L<sup>T</sup>L'''と'''LL<sup>T</sup>'''の固有値。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | HITSではクエリをもらったらまずランクの高いページを200程度集め、そのページからリンクされる、およびリンクするページを増やして初期集合を形成する。この集合から作成した引用行列'''L'''を、単位ベクトルを初期値としたた'''a''', '''h'''がそれぞれ収束するまで掛け算する。 | |
===利点と欠点=== | ===利点と欠点=== | ||
初期集合を形成する際に、余計なページを含むことでTopic driftとよばれるテーマの移動が起こってしまう。またスパムに対して弱い(ハブを簡単に偽装できる)。そのかわり、与えられたキーワードについて関連する重要ページを発見できる利点を持つ。 | 初期集合を形成する際に、余計なページを含むことでTopic driftとよばれるテーマの移動が起こってしまう。またスパムに対して弱い(ハブを簡単に偽装できる)。そのかわり、与えられたキーワードについて関連する重要ページを発見できる利点を持つ。 | ||
| + | |||
| + | ==共引用と書誌結合== | ||
| + | 文献計量学 (Bibliometrics) においては上記の'''L<sup>T</sup>L'''と'''LL<sup>T</sup>'''を共引用 (co-citation) および書誌結合 (bibliographic coupling) 行列と呼ぶ。 | ||
| + | |||
| + | 文献''i''が''j''を引用するとき''ij''成分を1、それ以外は0と定義した正方行列'''L'''(引用行列)を考えたとき、文献''i''と''j''を同時に引用する文献の数は<math>\textstyle C_{ij}=C_{ji}=\sum^n_{k=1}L_{ki}L_{kj}</math>とあらわされる。これは'''L<sup>T</sup>L'''に対応し、'''C=L<sup>T</sup>L'''を共引用行列と呼ぶ。 | ||
| + | |||
| + | 書誌結合関係とは共引用関係と対を成す概念である。文献''i''と''j''がともに同じ文献を引用するとき、''i''と''j''は書誌結合関係にあるという。文献''i''と''j''に同時に引用される文献の数は<math>\textstyle B_{ij}=B_{ji}=\sum^n_{k=1}L_{ik}L_{jk}</math>とあらわされる。 | ||
| + | これは'''LL<sup>T</sup>'''に対応し、'''B=LL<sup>T</sup>'''を共引用行列と呼ぶ。 | ||
| + | オーソリティ度は共引用行列の固有値、ハブ度は書誌結合行列の固有値にたいおうする。 | ||
==ウェブコミュニティ== | ==ウェブコミュニティ== | ||
Revision as of 15:07, 23 April 2009
Contents |
歴史
- 1998 Jan: J. KleinbergがHITSアルゴリズムを発表(9th ACM-SIAM DA)
- 1998 Apr: S. Brin, L. PageがPageRankを発表(7th WWW)
Centrality
無向グラフにおいて、頂点のネットワーク中心への近さを示す尺度を中心度(centrality)という。いずれの値も0-1の間をとるようにスケーリングする。有向グラフには次に述べるprestigeを使った方がよい。
- Degree centrality ... 辺数が多い点を中心と考える。
- Closeness centrality ... 全頂点への平均最短距離が短い点を中心と考える。
- Betweenness centrality ... 全頂点間の最短経路に多く使われる点を中心と考える。同じ値で辺のbetweennessも定義できる。
-
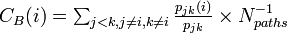 ただし
ただし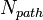 は
は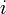 を除いたネットワーク中の最短経路
を除いたネットワーク中の最短経路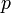 の本数で
の本数で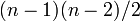 。
。
-
Prestige
有向グラフにおいて頂点の傑出具合を測る尺度を傑出度(prestige)という。
- Degree prestige ... 多くの入力辺がある点を傑出していると考える。
- Proximity prestige ... より多くの頂点から到達できる点を傑出していると考える。Degree prestigeの拡張になっている。
-
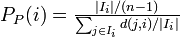 ただし>
ただし>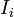 は
は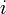 より到達できる頂点集合。
より到達できる頂点集合。
-
- Rank prestige ... 高いランクの頂点に指されている頂点もランクが高いと考える。
- PR=ATPR ただしPRは長さ
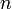 の縦ベクトル、Aは隣接行列。つまりPRはAの固有値にあたる。
の縦ベクトル、Aは隣接行列。つまりPRはAの固有値にあたる。
- PR=ATPR ただしPRは長さ
PageRank
Rank prestigeにおいてAを単なる隣接行列ではなく各頂点の次数(degree)で行方向にスケーリングした値、すなわち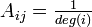 としたものをPageRankと呼ぶ。
つまり、行列Aを、ウェブページを訪れるユーザがページ内のリンクを等確率でクリックして次ページに移動するマルコフ過程の遷移行列と考え、PageRankはその定常分布に相当する。
としたものをPageRankと呼ぶ。
つまり、行列Aを、ウェブページを訪れるユーザがページ内のリンクを等確率でクリックして次ページに移動するマルコフ過程の遷移行列と考え、PageRankはその定常分布に相当する。
しかしこのままでは実用上以下の問題点がある。
- マルコフ過程の定常分布は、全ての状態が再帰的(recurrent)、つまり有限のステップで同じ状態に戻ってくることが可能でないと求まらない。つまり、どのページからも外に出るリンクがないとランクを付与できないページが生じる。
- ページ間のネットワークが強連結(strongly connected)でないと定常分布における確率が0となる頂点が生じてしまう。
- 遷移過程に周期性が存在すると、定常分布として収束しない。
これらの問題点を回避するため、ユーザはリンク先の無いページからは他の全ページに等確率で移動し、リンク先を持つページからも一定確率でランダムに他ページに移動すると仮定する。つまり
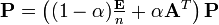 ここで行列Eは要素が全て1の正方行列。またパラメータαをdamping factorと呼び、
ここで行列Eは要素が全て1の正方行列。またパラメータαをdamping factorと呼び、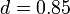 程度が用いられる。
程度が用いられる。
利点と欠点
ページランクはパラメータを持たない固定値のため事前に計算しておくことが可能。スパムに対しても頑健。 ただ、問い合わせの内容を一切考慮しないのは欠点ともいえる。
HITS
Hypertext Induced Topic Search(HITS)はオーソリティおよびハブと呼ばれる二種の頂点集合からなる二部グラフを求めるアルゴリズム。 オーソリティとは入力辺を多く持つページで多くのハブからリンクされる。 ハブとは出力辺を多く持つページで多くのオーソリティへリンクする。 各頂点におけるオーソリティとハブの次数をあらわす縦ベクトルはそれぞれa = LTh, h = La とあらわされる。つまり a = LTLa, h = LLTh となる。つまりaとhはそれぞれLTLとLLTの固有値。
HITSではクエリをもらったらまずランクの高いページを200程度集め、そのページからリンクされる、およびリンクするページを増やして初期集合を形成する。この集合から作成した引用行列Lを、単位ベクトルを初期値としたたa, hがそれぞれ収束するまで掛け算する。
利点と欠点
初期集合を形成する際に、余計なページを含むことでTopic driftとよばれるテーマの移動が起こってしまう。またスパムに対して弱い(ハブを簡単に偽装できる)。そのかわり、与えられたキーワードについて関連する重要ページを発見できる利点を持つ。
共引用と書誌結合
文献計量学 (Bibliometrics) においては上記のLTLとLLTを共引用 (co-citation) および書誌結合 (bibliographic coupling) 行列と呼ぶ。
文献iがjを引用するときij成分を1、それ以外は0と定義した正方行列L(引用行列)を考えたとき、文献iとjを同時に引用する文献の数は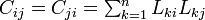 とあらわされる。これはLTLに対応し、C=LTLを共引用行列と呼ぶ。
とあらわされる。これはLTLに対応し、C=LTLを共引用行列と呼ぶ。
書誌結合関係とは共引用関係と対を成す概念である。文献iとjがともに同じ文献を引用するとき、iとjは書誌結合関係にあるという。文献iとjに同時に引用される文献の数は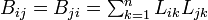 とあらわされる。
これはLLTに対応し、B=LLTを共引用行列と呼ぶ。
オーソリティ度は共引用行列の固有値、ハブ度は書誌結合行列の固有値にたいおうする。
とあらわされる。
これはLLTに対応し、B=LLTを共引用行列と呼ぶ。
オーソリティ度は共引用行列の固有値、ハブ度は書誌結合行列の固有値にたいおうする。
ウェブコミュニティ
ハブとオーソリティの関係のように、特定のトピックについて密に関連したページ集合をコミュニティと呼ぶ。(定義はさまざまある。) いくつかの例を挙げる。
- 二部グラフコミュニティ ... 完全二部グラフを探すアルゴリズムで探索できる (HITS 1998)
- 最大流コミュニティ ... 最大流アルゴリズムを用いてボトルネックを探し、ネットワークを切断してゆくことで探索できる (Flake et al. IEEE Computer 35(3) 2002)
- 辺betweennessコミュニティ ... betweennessが大きい辺から順番に除いていく
いずれもコミュニティの定義がはっきりしないので適当な時点でイテレーションを停止するしかない。