Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model

Latest revision as of 11:13, 3 August 2017

[edit] 学習事項

Erdős–Rényiグラフは、無向のランダムグラフ、頂点の次数分布は二項分布になる。
ポアソン分布による近似とその必要性。

[edit] 歴史と参考図書

Erdős P, Rényi A. "On Random Graphs. I.". Publicationes Mathematicae 6:290–297, 1959
Erdős P, Rényi A. "The Evolution of Random Graphs". Publ. Math. Inst. Hung. Acad. Sci 5:17–61, 1960
Bollobás B. Random Graphs (2nd ed.), Cambridge University Press, 2001
Durrett R. Random Graph Dynamics, Cambridge University Press, 2004

[edit] Erdős–Rényiグラフ

全ての頂点間に一定の確率 p で独立に辺を作成してできるランダムグラフをErdős–Rényi (ER) グラフと呼びます。各頂点に注目してみると　n -1 点に対して確率 p で辺を張るため、その次数は二項分布

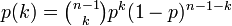
$\textstyle p(k) = \binom{n-1}{k} p^k (1-p)^{n-1-k}$

に従います。

ERモデルにおいて、辺の数を正確に N 本とする場合を考えることもできます。n 頂点からランダムに2つを選び、その間に辺を作成するプロセスを正確に N 回繰り返します。(ランダムに頂点を選ぶ回数は m = 2 N。)これは次数の期待値が p = 2 N / n(n -1) のERグラフにおいて、たまたま辺数が N となった場合に相当します。

[edit] 次数の分布

各頂点についてみると、n -1 点に対して確率 p で辺を張るため平均次数は ( n -1) p です。次数分布は二項分布になりますが、このままだと n　を大きくすればいくらでも次数の大きな頂点が存在してしまいます。しかし、現実のネットワークでは次数に上限がある場合がほとんどです。そのため、サイズがどんなに大きくなっても各頂点の次数は平均的に一定値という仮定をします。

n →　∞, p → 0、 (n - 1) p → c (正定数)

このとき、二項分布はポアソン分布で近似できます。

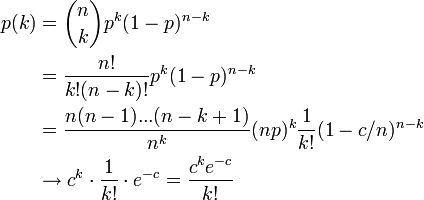
$\textstyle \begin{align} \textstyle p(k) &= \binom{n}{k} p^k (1-p)^{n-k} \\ &= \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k} \\ &= \frac{n(n-1) ... (n -k +1)}{n^k} (np)^k \frac{1}{k!} (1- c/n)^{n-k} \\ &\rightarrow c^k \cdot \frac{1}{k!} \cdot e^{-c} = \frac{c^k e^{-c}}{k!} \end{align}$

ここで c は次数 k の平均値 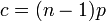$c = (n-1)p$ です。k が大きい場合、ポアソン分布は小さな値をとります。つまり、ハブ頂点はできにくくなります。

[edit] ネットワークの進化

次数の平均値 c = ( n -1) p を変化させて生じるグラフ形状の違いを検証します。

c << 1 / n² のとき

生成される辺数の期待値は pn (n -1) / 2 = cn/ 2 になります。n を無限大にしたとき、この値が 0 に近づくのでネットワークのサイズに対してほとんど辺を持たないことになります。

c = 1 / n のとき

上と同じ理由で、ネットワーク全体で辺が定数本だけ作られるネットワークになります。ほとんどの辺がばらばらに存在します。

c = const.

各頂点が一定数の辺を持つことを意味します。　ちょうど c = 1 だと二部グラフのマッチングです。c = 2 だと閉路の集合になります。

各頂点が持つ辺の本数（の期待値）が c なので、c < 1 のときは連結部分の大きさが高々　log n 程度にしかなりません。しかし　c > 1 としたとたん、繋がっていく確率のほうが高くなります。その半径 (diameter) を k とおくと c^k = n まで成長できるので k = log n / log c です。

詳細な解析によると、臨界点にあたる c = 1 では連結部分のサイズが O (n ^2/3) になることが知られています。

c = log n

全体が連結になります。ある頂点が辺を全く持たない確率を考えると (1 - p)^{n - 1} = { ( 1 - c /(n - 1))^{(n - 1)/c} }^c <= e^-c。したがって、そのような頂点がグラフ中に存在してしまう確率の上限は ne^-c となります。これを 0 に収束させるには例えば c >= 2 log n で十分です。このとき孤立点は消滅しています。

相転移

上でみたように、次数の平均値が 1 をこえると急に連結成分のサイズが大きくなり、 log n に達すると全体が連結になります。こうした点を、相転移点と呼びます。

@@ Line 1: / Line 1: @@
-{{Lecture/Header}}
+__TOC__
+==学習事項==
+* Erdős–Rényiグラフは、無向のランダムグラフ、頂点の次数分布は二項分布になる。
+* ポアソン分布による近似とその必要性。
-ここでは頂点がすべて連結した無向グラフを扱う。
 ==歴史と参考図書==
@@ Line 9: / Line 12: @@
 * Durrett R. Random Graph Dynamics, Cambridge University Press, 2004
-==ネットワークの指標:<math>C</math>と<math>L</math>==
+==Erdős–Rényiグラフ==
-ネットワーク全体についての尺度として、クラスター係数<math>C</math>と平均頂点間距離<math>L</math>を紹介する。
-===クラスター係数===
+全ての頂点間に一定の確率 ''p'' で独立に辺を作成してできるランダムグラフをErdős–Rényi (ER) グラフと呼びます。各頂点に注目してみると　''n'' -1 点に対して確率 ''p'' で辺を張るため、その次数は二項分布
-クラスター係数は隣接する頂点間の辺の密度の平均値にあたる。
-まず各頂点 ''i'' におけるクラスター係数 <math>C_i</math> を以下のように定義する。
-辺の長さはすべて1とし <math>|e|=1</math>、頂点 ''i'' の次数を ''deg''(''i''), 隣接する頂点群を ''adj''(''i'') と書く。
-:<math>\textstyle C_i=\frac{2}{deg(i)(deg(i)-1)} \sum_{j,k \in adj(i)} |e_{jk}|</math>
+<math>\textstyle p(k) = \binom{n-1}{k} p^k (1-p)^{n-1-k}</math>
-グラフ全体のクラスター係数はその平均値になる。
+に従います。
-:<math>\textstyle C =\frac{1}{n} \sum^{n}_{i=1}C_i</math>
+ERモデルにおいて、辺の数を正確に ''N'' 本とする場合を考えることもできます。''n'' 頂点からランダムに2つを選び、その間に辺を作成するプロセスを正確に ''N'' 回繰り返します。(ランダムに頂点を選ぶ回数は ''m'' = 2 ''N''。)これは次数の期待値が ''p'' = 2 ''N'' / ''n''(''n'' -1) のERグラフにおいて、たまたま辺数が ''N'' となった場合に相当します。
-===平均頂点間距離===
+===次数の分布===
-平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点<math>i, j</math>間の最短経路を<math>p_{ij}</math>と書く。各点に注目する場合は、距離<math>L</math>以内にある頂点数を数えることで求められる。
+各頂点についてみると、''n'' -1 点に対して確率 ''p'' で辺を張るため平均次数は ( ''n'' -1) ''p'' です。
-:<math>\textstyle L=\frac{1}{n} \sum_{i,j\in G}|p_{ij}|</math>
+次数分布は二項分布になりますが、このままだと ''n''　を大きくすればいくらでも次数の大きな頂点が存在してしまいます。
+しかし、現実のネットワークでは次数に上限がある場合がほとんどです。
+そのため、サイズがどんなに大きくなっても各頂点の次数は平均的に一定値という仮定をします。
-===様々なグラフにおける<math>C</math>と<math>L</math>===
+''n'' →　∞, ''p'' → 0、 (''n'' - 1) ''p'' → c  (正定数)
-====完全グラフ====
-全ての頂点間に辺を持つグラフは<math>C=L=1</math>。
-====格子====
+このとき、二項分布はポアソン分布で近似できます。
-平面の場合は三角格子、正方格子が考えられる。特に、<math>d</math>次元空間において辺の長さが単位距離の格子を'''Z'''<sup>d</sup>と書く。
-:例. '''Z'''<sup>2</sup>において、<math>deg(i)=2d</math>
-定義のままだとクラスター係数が0になって面白くないので、最短距離が<math>a</math>以下の点には全て辺を張るバリエーション'''Z''''<sup>d</sup>を考えよう。
+<math>\textstyle
-:例. '''Z''''<sup>d</sup>のクラスター係数は<math>\textstyle C=\frac{3(a-1)}{2(2a-1)}</math>、平均頂点間距離は<math>\textstyle L=\sqrt[d]{n}/a</math>
+\begin{align} \textstyle
+p(k) &= \binom{n}{k} p^k (1-p)^{n-k}  \\
+&= \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k} \\
+&= \frac{n(n-1) ... (n -k +1)}{n^k} (np)^k  \frac{1}{k!} (1- c/n)^{n-k} \\
+&\rightarrow c^k \cdot \frac{1}{k!} \cdot e^{-c} = \frac{c^k e^{-c}}{k!}
+\end{align}
+</math>
-====木====
+ここで ''c'' は次数 ''k'' の平均値 <math>c = (n-1)p</math> です。''k'' が大きい場合、ポアソン分布は小さな値をとります。つまり、ハブ頂点はできにくくなります。
-簡単のため全頂点が同じ次数を持つ木を考える。中心の頂点<math>v_0</math>を根(root)と呼ぶ。木はその定義よりサイクルを持たないので<math>C=0</math>。また平均頂点間距離は、距離L以内にある頂点を数えることで求められる。
-:<math>n = 1 + d + d(d-1) + ... + d(d-1)^L = 1 +d (1-(d-1)^{L+1})/(1-(d-1))</math>∝<math>(d-1)^{L+1}</math>
-すなわち
-:<math>\textstyle L=\propto \frac{\log n}{\log (d-1)} \propto \log n</math>
-==Erdős–Rényiグラフ==
+===ネットワークの進化===
-全ての頂点間に一定の確率<math>p</math>で独立に辺を作成してできるランダムグラフをErdős–Rényiグラフと呼ぶ。各頂点に注目してみると<math>n-1</math>点に対して確率<math>p</math>で辺を張るため、次数は二項分布
+次数の平均値 ''c'' = ( ''n'' -1) ''p'' を変化させて生じるグラフ形状の違いを検証します。
-<math>{}_{n-1}\mbox{C}_k p^k(1-p)^{n-1-k}</math>
+* ''c'' << 1 / ''n''<sup>2</sup> のとき
-に従う。すなわち次数の平均は<math>c = (n-1)p</math>と書ける。
+生成される辺数の期待値は ''pn'' (''n'' -1) / 2 = ''cn''/ 2 になります。''n'' を無限大にしたとき、この値が 0 に近づくのでネットワークのサイズに対してほとんど辺を持たないことになります。
-===ネットワークの進化===
+* ''c'' = 1 / ''n'' のとき
-次数の平均値<math>c</math>を変化させて生じるグラフ形状の違いを検証しよう。
+上と同じ理由で、ネットワーク全体で辺が定数本だけ作られるネットワークになります。ほとんどの辺がばらばらに存在します。
-;<math>\textstyle c \le \frac{1}{n^2} </math>
-辺の生成される確率が<math>pn(n-1)/2 = cn/2 \xrightarrow{n\rarr \infty} 0</math>になるため、辺を持たない。
-;<math>\textstyle c = 1/\sqrt{n}</math>
+* ''c'' = const.
-辺があったとしても木にしかならない。
+各頂点が一定数の辺を持つことを意味します。　ちょうど ''c'' = 1 だと二部グラフのマッチングです。''c'' = 2 だと閉路の集合になります。
-;<math>\textstyle c = const.</math>
+各頂点が持つ辺の本数（の期待値）が ''c'' なので、''c'' < 1 のときは連結部分の大きさが高々　log ''n'' 程度にしかなりません。しかし　''c'' > 1 としたとたん、繋がっていく確率のほうが高くなります。その半径 (diameter) を ''k'' とおくと ''c''<sup>k</sup> = ''n'' まで成長できるので ''k'' = log ''n'' / log ''c'' です。
-各頂点が定数本の辺を持ちはじめる。
-*ちょうど<math>c=1</math>だと二部グラフのマッチング、<math>c=2</math>だと閉路の集合になる。
-*各頂点が持つ辺の本数（の期待値）が<math>c</math>なので、<math>c < 1</math>のとき連結部分の大きさは高々<math>\log n</math>程度にしかならない。しかし<math>c > 1</math>の場合繋がっていく確率のほうが高く、その半径(diameter)を<math>k</math>とおくと<math>c^k=n</math>まで成長できる。このとき<math>k=\log n / \log c</math>。
-*詳細な解析によると、臨界点にあたる<math>c = 1</math>では連結部分のサイズが<math>O(n^{2/3})</math>になることが知られている。
-;<math>\textstyle c = \log n</math>
+詳細な解析によると、臨界点にあたる ''c'' = 1 では連結部分のサイズが ''O'' (''n'' <sup>2/3</sup>) になることが知られています。
-全体が連結になる。ある頂点が辺を全く持たない確率は<math>\textstyle (1-p)^{n-1}=((1-\frac{c}{n-1})^{\frac{n-1}{c}})^{c} \leq e^{-c}</math>。したがって、そのような頂点がグラフ中に存在しない確率の上限は<math>ne^{-c}</math>となる。これを0に収束させるには例えば<math>c \geq 2 \log n</math>で十分である。このとき孤立点が消滅する。
-===辺の数を固定するモデル===
+* ''c'' = log ''n''
-辺の数を正確に<math>N</math>本とする場合を考えよう。<math>n</math>頂点からランダムに2つを選び、その間に辺を作成するプロセスを正確に<math>N</math>回繰り返す。(ランダムに頂点を選ぶ回数は<math>m = 2N</math>。)これは次数の期待値が<math>p=2N/n(n-1)</math>のERグラフにおいて、ちょうど辺数が<math>N</math>となった場合に相当する。
+全体が連結になります。ある頂点が辺を全く持たない確率を考えると
+(1 - ''p'')<sup>''n'' - 1</sup> = { ( 1 - c /(''n'' - 1))<sup>(''n'' - 1)/c</sup> }<sup>''c''</sup> <= ''e''<sup>-''c''</sup>。したがって、そのような頂点がグラフ中に存在してしまう確率の上限は ''ne''<sup>-''c''</sup> となります。これを 0 に収束させるには例えば ''c'' >= 2 log ''n'' で十分です。このとき孤立点は消滅しています。
-===ネットワークの特徴===
+;相転移
-;クラスター係数
+上でみたように、次数の平均値が 1 をこえると急に連結成分のサイズが大きくなり、 log ''n'' に達すると全体が連結になります。
-:辺が張られる確率は全て独立なので<math>C(p)=p \simeq c /n</math>。これは<math>K_3</math>や<math>K_4</math>をあまり含まないことを意味している。
+こうした点を、相転移点と呼びます。
-;平均頂点間距離
-:各頂点が持つ辺の期待値を<math>c = (n-1)p</math>として<math>L(p) \geq \log n / \log c = O(\log n)</math>。
-;連結性
-:Erdős–Rényiグラフ全体が連結であるためには次数が<math>O(\log n)</math>以上必要。

Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model

Latest revision as of 11:13, 3 August 2017

Contents

[edit] 学習事項

[edit] 歴史と参考図書

[edit] Erdős–Rényiグラフ

[edit] 次数の分布

[edit] ネットワークの進化

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

metabolites

Toolbox