Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model
m |
m (→ネットワークの進化) |
||
| (33 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | __TOC__ | |
| − | = | + | ==学習事項== |
| − | * | + | * Erdős–Rényiグラフは、無向のランダムグラフ、頂点の次数分布は二項分布になる。 |
| + | * ポアソン分布による近似とその必要性。 | ||
| − | |||
| − | |||
| − | == | + | ==歴史と参考図書== |
| − | + | * Erdős P, Rényi A. "On Random Graphs. I.". Publicationes Mathematicae 6:290–297, 1959 | |
| − | : | + | * Erdős P, Rényi A. "The Evolution of Random Graphs". Publ. Math. Inst. Hung. Acad. Sci 5:17–61, 1960 |
| − | + | * Bollobás B. Random Graphs (2nd ed.), Cambridge University Press, 2001 | |
| − | + | * Durrett R. Random Graph Dynamics, Cambridge University Press, 2004 | |
| − | == | + | ==Erdős–Rényiグラフ== |
| − | + | ||
| − | + | ||
| − | + | 全ての頂点間に一定の確率 ''p'' で独立に辺を作成してできるランダムグラフをErdős–Rényi (ER) グラフと呼びます。各頂点に注目してみると ''n'' -1 点に対して確率 ''p'' で辺を張るため、その次数は二項分布 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <math>\textstyle p(k) = \binom{n-1}{k} p^k (1-p)^{n-1-k}</math> | |
| − | + | ||
| − | + | に従います。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | = | + | ERモデルにおいて、辺の数を正確に ''N'' 本とする場合を考えることもできます。''n'' 頂点からランダムに2つを選び、その間に辺を作成するプロセスを正確に ''N'' 回繰り返します。(ランダムに頂点を選ぶ回数は ''m'' = 2 ''N''。)これは次数の期待値が ''p'' = 2 ''N'' / ''n''(''n'' -1) のERグラフにおいて、たまたま辺数が ''N'' となった場合に相当します。 |
| − | + | ||
| − | == | + | ===次数の分布=== |
| − | + | 各頂点についてみると、''n'' -1 点に対して確率 ''p'' で辺を張るため平均次数は ( ''n'' -1) ''p'' です。 | |
| − | + | 次数分布は二項分布になりますが、このままだと ''n'' を大きくすればいくらでも次数の大きな頂点が存在してしまいます。 | |
| − | + | しかし、現実のネットワークでは次数に上限がある場合がほとんどです。 | |
| − | + | そのため、サイズがどんなに大きくなっても各頂点の次数は平均的に一定値という仮定をします。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ''n'' → ∞, ''p'' → 0、 (''n'' - 1) ''p'' → c (正定数) | |
| − | == | + | このとき、二項分布はポアソン分布で近似できます。 |
| − | + | ||
| − | == | + | <math>\textstyle |
| + | \begin{align} \textstyle | ||
| + | p(k) &= \binom{n}{k} p^k (1-p)^{n-k} \\ | ||
| + | &= \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k} \\ | ||
| + | &= \frac{n(n-1) ... (n -k +1)}{n^k} (np)^k \frac{1}{k!} (1- c/n)^{n-k} \\ | ||
| + | &\rightarrow c^k \cdot \frac{1}{k!} \cdot e^{-c} = \frac{c^k e^{-c}}{k!} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | ここで ''c'' は次数 ''k'' の平均値 <math>c = (n-1)p</math> です。''k'' が大きい場合、ポアソン分布は小さな値をとります。つまり、ハブ頂点はできにくくなります。 | ||
| + | |||
| + | ===ネットワークの進化=== | ||
| + | 次数の平均値 ''c'' = ( ''n'' -1) ''p'' を変化させて生じるグラフ形状の違いを検証します。 | ||
| + | |||
| + | * ''c'' << 1 / ''n''<sup>2</sup> のとき | ||
| + | |||
| + | 生成される辺数の期待値は ''pn'' (''n'' -1) / 2 = ''cn''/ 2 になります。''n'' を無限大にしたとき、この値が 0 に近づくのでネットワークのサイズに対してほとんど辺を持たないことになります。 | ||
| + | |||
| + | * ''c'' = 1 / ''n'' のとき | ||
| + | 上と同じ理由で、ネットワーク全体で辺が定数本だけ作られるネットワークになります。ほとんどの辺がばらばらに存在します。 | ||
| + | |||
| + | * ''c'' = const. | ||
| + | 各頂点が一定数の辺を持つことを意味します。 ちょうど ''c'' = 1 だと二部グラフのマッチングです。''c'' = 2 だと閉路の集合になります。 | ||
| + | |||
| + | 各頂点が持つ辺の本数(の期待値)が ''c'' なので、''c'' < 1 のときは連結部分の大きさが高々 log ''n'' 程度にしかなりません。しかし ''c'' > 1 としたとたん、繋がっていく確率のほうが高くなります。その半径 (diameter) を ''k'' とおくと ''c''<sup>k</sup> = ''n'' まで成長できるので ''k'' = log ''n'' / log ''c'' です。 | ||
| + | |||
| + | 詳細な解析によると、臨界点にあたる ''c'' = 1 では連結部分のサイズが ''O'' (''n'' <sup>2/3</sup>) になることが知られています。 | ||
| + | |||
| + | * ''c'' = log ''n'' | ||
| + | 全体が連結になります。ある頂点が辺を全く持たない確率を考えると | ||
| + | (1 - ''p'')<sup>''n'' - 1</sup> = { ( 1 - c /(''n'' - 1))<sup>(''n'' - 1)/c</sup> }<sup>''c''</sup> <= ''e''<sup>-''c''</sup>。したがって、そのような頂点がグラフ中に存在してしまう確率の上限は ''ne''<sup>-''c''</sup> となります。これを 0 に収束させるには例えば ''c'' >= 2 log ''n'' で十分です。このとき孤立点は消滅しています。 | ||
| + | |||
| + | ;相転移 | ||
| + | 上でみたように、次数の平均値が 1 をこえると急に連結成分のサイズが大きくなり、 log ''n'' に達すると全体が連結になります。 | ||
| + | こうした点を、相転移点と呼びます。 | ||
Latest revision as of 11:13, 3 August 2017
Contents |
[edit] 学習事項
- Erdős–Rényiグラフは、無向のランダムグラフ、頂点の次数分布は二項分布になる。
- ポアソン分布による近似とその必要性。
[edit] 歴史と参考図書
- Erdős P, Rényi A. "On Random Graphs. I.". Publicationes Mathematicae 6:290–297, 1959
- Erdős P, Rényi A. "The Evolution of Random Graphs". Publ. Math. Inst. Hung. Acad. Sci 5:17–61, 1960
- Bollobás B. Random Graphs (2nd ed.), Cambridge University Press, 2001
- Durrett R. Random Graph Dynamics, Cambridge University Press, 2004
[edit] Erdős–Rényiグラフ
全ての頂点間に一定の確率 p で独立に辺を作成してできるランダムグラフをErdős–Rényi (ER) グラフと呼びます。各頂点に注目してみると n -1 点に対して確率 p で辺を張るため、その次数は二項分布
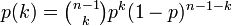
に従います。
ERモデルにおいて、辺の数を正確に N 本とする場合を考えることもできます。n 頂点からランダムに2つを選び、その間に辺を作成するプロセスを正確に N 回繰り返します。(ランダムに頂点を選ぶ回数は m = 2 N。)これは次数の期待値が p = 2 N / n(n -1) のERグラフにおいて、たまたま辺数が N となった場合に相当します。
[edit] 次数の分布
各頂点についてみると、n -1 点に対して確率 p で辺を張るため平均次数は ( n -1) p です。 次数分布は二項分布になりますが、このままだと n を大きくすればいくらでも次数の大きな頂点が存在してしまいます。 しかし、現実のネットワークでは次数に上限がある場合がほとんどです。 そのため、サイズがどんなに大きくなっても各頂点の次数は平均的に一定値という仮定をします。
n → ∞, p → 0、 (n - 1) p → c (正定数)
このとき、二項分布はポアソン分布で近似できます。
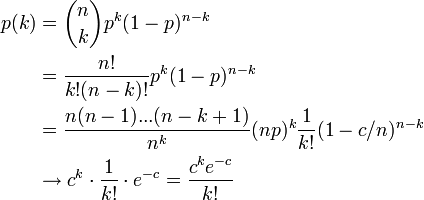
ここで c は次数 k の平均値 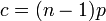 です。k が大きい場合、ポアソン分布は小さな値をとります。つまり、ハブ頂点はできにくくなります。
です。k が大きい場合、ポアソン分布は小さな値をとります。つまり、ハブ頂点はできにくくなります。
[edit] ネットワークの進化
次数の平均値 c = ( n -1) p を変化させて生じるグラフ形状の違いを検証します。
- c << 1 / n2 のとき
生成される辺数の期待値は pn (n -1) / 2 = cn/ 2 になります。n を無限大にしたとき、この値が 0 に近づくのでネットワークのサイズに対してほとんど辺を持たないことになります。
- c = 1 / n のとき
上と同じ理由で、ネットワーク全体で辺が定数本だけ作られるネットワークになります。ほとんどの辺がばらばらに存在します。
- c = const.
各頂点が一定数の辺を持つことを意味します。 ちょうど c = 1 だと二部グラフのマッチングです。c = 2 だと閉路の集合になります。
各頂点が持つ辺の本数(の期待値)が c なので、c < 1 のときは連結部分の大きさが高々 log n 程度にしかなりません。しかし c > 1 としたとたん、繋がっていく確率のほうが高くなります。その半径 (diameter) を k とおくと ck = n まで成長できるので k = log n / log c です。
詳細な解析によると、臨界点にあたる c = 1 では連結部分のサイズが O (n 2/3) になることが知られています。
- c = log n
全体が連結になります。ある頂点が辺を全く持たない確率を考えると (1 - p)n - 1 = { ( 1 - c /(n - 1))(n - 1)/c }c <= e-c。したがって、そのような頂点がグラフ中に存在してしまう確率の上限は ne-c となります。これを 0 に収束させるには例えば c >= 2 log n で十分です。このとき孤立点は消滅しています。
- 相転移
上でみたように、次数の平均値が 1 をこえると急に連結成分のサイズが大きくなり、 log n に達すると全体が連結になります。 こうした点を、相転移点と呼びます。