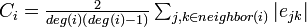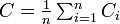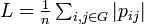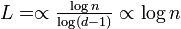Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model
From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology(Difference between revisions)
m |
m |
||
| Line 2: | Line 2: | ||
=歴史= | =歴史= | ||
| − | * 1998 | + | * 1998 Watts DJ, Strogatz S "Collective dynamics of 'small-world' networks". Nature 393: 440–442. [http://web.archive.org/web/20070418032327/http://www.tam.cornell.edu/SS_nature_smallworld.pdf. doi:10.1038/30918.] |
| + | |||
| + | =ネットワークの指標:<math>C</math>と<math>L</math>= | ||
| + | ネットワーク全体についての尺度として、クラスター係数<math>C</math>と平均頂点間距離<math>L</math>を紹介する。 | ||
| − | |||
| − | |||
==クラスター係数== | ==クラスター係数== | ||
| − | クラスター係数は隣接する頂点間の辺の密度の平均値にあたる。まず各頂点<math>i</math> | + | クラスター係数は隣接する頂点間の辺の密度の平均値にあたる。まず各頂点<math>i</math>におけるクラスター係数<math>C_i</math>を以下のように定義する。辺の長さはすべて1とする<math>|e|=1</math>。 |
:<math>\textstyle C_i=\frac{2}{deg(i)(deg(i)-1)} \sum_{j,k \in neighbor(i)} |e_{jk}|</math> | :<math>\textstyle C_i=\frac{2}{deg(i)(deg(i)-1)} \sum_{j,k \in neighbor(i)} |e_{jk}|</math> | ||
グラフ全体のクラスター係数はその平均値になる。 | グラフ全体のクラスター係数はその平均値になる。 | ||
| Line 13: | Line 14: | ||
==平均頂点間距離== | ==平均頂点間距離== | ||
| − | 平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点<math>i, j</math>間の最短経路を<math>p_{ij}</math> | + | 平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点<math>i, j</math>間の最短経路を<math>p_{ij}</math>と書く。各点に注目する場合は、距離<math>L</math>以内にある頂点数を数えることで求められる。 |
:<math>\textstyle L=\frac{1}{n} \sum_{i,j\in G}|p_{ij}|</math> | :<math>\textstyle L=\frac{1}{n} \sum_{i,j\in G}|p_{ij}|</math> | ||
| − | == | + | ==様々なグラフにおける<math>C</math>と<math>L</math>== |
===完全グラフ=== | ===完全グラフ=== | ||
全ての頂点間に辺を持つグラフは<math>C=L=1</math>。 | 全ての頂点間に辺を持つグラフは<math>C=L=1</math>。 | ||
| Line 23: | Line 24: | ||
:例. '''Z'''<sup>2</sup>において、<math>deg(i)=2d</math> | :例. '''Z'''<sup>2</sup>において、<math>deg(i)=2d</math> | ||
| − | + | 定義のままだとクラスター係数が0になって面白くないので、最短距離が<math>a</math>以下の点には全て辺を張るバリエーション'''Z''''<sup>d</sup>を考えよう。 | |
:例. '''Z''''<sup>d</sup>のクラスター係数は<math>\textstyle C=\frac{3(a-1)}{2(2a-1)}</math>、平均頂点間距離は<math>\textstyle L=\sqrt[d]{n}/a</math> | :例. '''Z''''<sup>d</sup>のクラスター係数は<math>\textstyle C=\frac{3(a-1)}{2(2a-1)}</math>、平均頂点間距離は<math>\textstyle L=\sqrt[d]{n}/a</math> | ||
===木=== | ===木=== | ||
| − | + | 簡単のため全頂点が同じ次数を持つ木を考える。中心の頂点<math>v_0</math>を根(root)と呼ぶ。木はその定義よりサイクルを持たないので<math>C=0</math>。また平均頂点間距離は、距離L以内にある頂点を数えることで求められる。 | |
:<math>n = 1 + d + d(d-1) + ... + d(d-1)^L = 1 +d (1-(d-1)^{L+1})/(1-(d-1))</math>∝<math>(d-1)^{L+1}</math> | :<math>n = 1 + d + d(d-1) + ... + d(d-1)^L = 1 +d (1-(d-1)^{L+1})/(1-(d-1))</math>∝<math>(d-1)^{L+1}</math> | ||
| − | + | すなわち | |
:<math>\textstyle L=\propto \frac{\log n}{\log (d-1)} \propto \log n</math> | :<math>\textstyle L=\propto \frac{\log n}{\log (d-1)} \propto \log n</math> | ||
=Erdős–Rényiグラフ= | =Erdős–Rényiグラフ= | ||
| − | + | 全ての頂点間に一定の確率<math>p</math>で独立に辺を作成してできるランダムグラフをErdős–Rényiグラフと呼ぶ。各頂点に注目してみると<math>n-1</math>点に対して確率<math>p</math>で辺を張るため、次数は二項分布<math>{}_{n-1}\mbox{C}_k p^k(1-p)^{n-1-k}</math>に従う。すなわち次数の平均は<math>c = (n-1)p</math>と書ける。 | |
==ネットワークの進化== | ==ネットワークの進化== | ||
| − | 次数の平均値<math>c</math> | + | 次数の平均値<math>c</math>を変化させて生じるグラフ形状の違いを検証しよう。 |
| − | ;<math>\textstyle c | + | ;<math>\textstyle c \leq \frac{1}{n^2} </math> |
| − | :辺の生成される確率が<math>pn(n-1)/2 \rarr 0</math>になるため、辺を持たない。 | + | :辺の生成される確率が<math>pn(n-1)/2 = cn/2 \xrightarrow{n\rarr \infty} 0</math>になるため、辺を持たない。 |
;<math>\textstyle c = 1/\sqrt{n}</math> | ;<math>\textstyle c = 1/\sqrt{n}</math> | ||
| − | : | + | :木が育ち始める。 |
;<math>\textstyle c = const.</math> | ;<math>\textstyle c = const.</math> | ||
| − | : | + | :各頂点が定数本の辺を持つ。ちょうど1本だと二部グラフのマッチング、2本だと閉路の集合になる。3本以上持ちはじめると下記に述べる特徴を持ち始める。ここで<math>c</math>を定数とおいたことで二項分布をポアソン近似した場合、次数は<math>\textstyle \frac{e^{-c}c^k}{k!}</math>に従う。平均値はもちろん<math>c</math>。 |
;<math>\textstyle c = \log n</math> | ;<math>\textstyle c = \log n</math> | ||
| − | : | + | :全体が連結になる。ある頂点が辺を全く持たない確率は<math>\textstyle (1-p)^{n-1}=((1-\frac{c}{n-1})^{\frac{n-1}{c}})^{c} \leq e^{-c}</math>。したがって、そのような頂点がグラフ中に存在しない確率の上限は<math>ne^{-c}</math>となり、これを0に収束させるには例えば<math>c \geq 2 \log n</math>で十分である。つまり、孤立点が消滅する。 |
| − | + | この結果より、Erdős–Rényiグラフが連結であるためには次数が<math>O(\log n)</math>以上必要であることを意味し、現実のネットワークのモデルとしてはあまり適切でないことがわかる。 | |
==クラスター係数== | ==クラスター係数== | ||
辺が張られる確率は全て独立なので<math>C=p \simeq c /n</math>。 | 辺が張られる確率は全て独立なので<math>C=p \simeq c /n</math>。 | ||
==平均頂点間距離== | ==平均頂点間距離== | ||
Revision as of 14:46, 7 May 2009
ここでは頂点がすべて連結した無向グラフを扱う。
Contents |
歴史
- 1998 Watts DJ, Strogatz S "Collective dynamics of 'small-world' networks". Nature 393: 440–442. doi:10.1038/30918.
ネットワークの指標: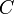
と
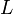
ネットワーク全体についての尺度として、クラスター係数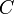と平均頂点間距離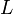を紹介する。
クラスター係数
クラスター係数は隣接する頂点間の辺の密度の平均値にあたる。まず各頂点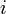
におけるクラスター係数
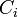を以下のように定義する。辺の長さはすべて1とする
。
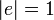グラフ全体のクラスター係数はその平均値になる。
平均頂点間距離
平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点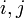
間の最短経路を
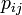と書く。各点に注目する場合は、距離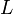以内にある頂点数を数えることで求められる。
様々なグラフにおける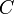と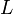
完全グラフ
全ての頂点間に辺を持つグラフは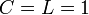
。
格子
平面の場合は三角格子、正方格子が考えられる。特に、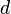
次元空間において辺の長さが単位距離の格子をZdと書く。
- 例. Z2において、
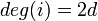
定義のままだとクラスター係数が0になって面白くないので、最短距離が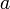
以下の点には全て辺を張るバリエーションZ'dを考えよう。
- 例. Z'dのクラスター係数は
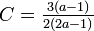、平均頂点間距離は![\textstyle L=\sqrt[d]{n}/a](/mediawiki/images/math/f/5/8/f583b41db535b1a73d0d831b87ea2808.png)
木
簡単のため全頂点が同じ次数を持つ木を考える。中心の頂点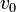
を根(root)と呼ぶ。木はその定義よりサイクルを持たないので
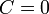。また平均頂点間距離は、距離L以内にある頂点を数えることで求められる。
∝
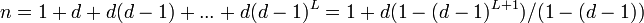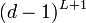
すなわち
Erdős–Rényiグラフ
全ての頂点間に一定の確率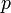
で独立に辺を作成してできるランダムグラフをErdős–Rényiグラフと呼ぶ。各頂点に注目してみると
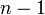点に対して確率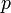で辺を張るため、次数は二項分布
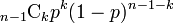に従う。すなわち次数の平均は
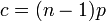と書ける。
ネットワークの進化
次数の平均値
を変化させて生じるグラフ形状の違いを検証しよう。
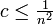
- 辺の生成される確率が
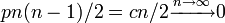になるため、辺を持たない。
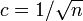
- 木が育ち始める。
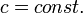
- 各頂点が定数本の辺を持つ。ちょうど1本だと二部グラフのマッチング、2本だと閉路の集合になる。3本以上持ちはじめると下記に述べる特徴を持ち始める。ここでを定数とおいたことで二項分布をポアソン近似した場合、次数は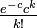
に従う。平均値はもちろん。
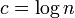
- 全体が連結になる。ある頂点が辺を全く持たない確率は
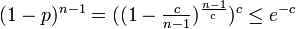。したがって、そのような頂点がグラフ中に存在しない確率の上限は
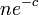となり、これを0に収束させるには例えば
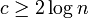で十分である。つまり、孤立点が消滅する。
この結果より、Erdős–Rényiグラフが連結であるためには次数が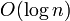
以上必要であることを意味し、現実のネットワークのモデルとしてはあまり適切でないことがわかる。
クラスター係数
辺が張られる確率は全て独立なので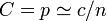
。
