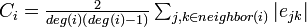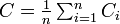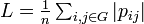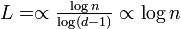Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model
From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology(Difference between revisions)
(New page: ここでは頂点がすべて連結した無向グラフを扱う。 =歴史= * 1998 D. J. Watts, Steven Strogatz "Collective dynamics of 'small-world' networks". Nature 393: 440–442. ...) |
m |
||
| Line 13: | Line 13: | ||
==平均頂点間距離== | ==平均頂点間距離== | ||
| − | 平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点<math>i, j</math>間の最短経路を<math>p_{ij}</math> | + | 平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点<math>i, j</math>間の最短経路を<math>p_{ij}</math>と書く。距離<math>L</math>以内にある頂点の数を数えることで求められる。 |
:<math>\textstyle L=\frac{1}{n} \sum_{i,j\in G}|p_{ij}|</math> | :<math>\textstyle L=\frac{1}{n} \sum_{i,j\in G}|p_{ij}|</math> | ||
==様々なグラフ== | ==様々なグラフ== | ||
| + | ===完全グラフ=== | ||
| + | 全ての頂点間に辺を持つグラフは<math>C=L=1</math>。 | ||
===格子=== | ===格子=== | ||
平面の場合は三角格子、正方格子が考えられる。特に、<math>d</math>次元空間において辺の長さが単位距離の格子を'''Z'''<sup>d</sup>と書く。 | 平面の場合は三角格子、正方格子が考えられる。特に、<math>d</math>次元空間において辺の長さが単位距離の格子を'''Z'''<sup>d</sup>と書く。 | ||
:例. '''Z'''<sup>2</sup>において、<math>deg(i)=2d</math> | :例. '''Z'''<sup>2</sup>において、<math>deg(i)=2d</math> | ||
| − | + | クラスター係数は定義のままだと0になって面白くないので、最短距離が<math>a</math>以下の点には全て辺を持つ'''Z''''<sup>d</sup>を考えよう。 | |
| − | :例. '''Z''''<sup>d</sup>のクラスター係数は | + | :例. '''Z''''<sup>d</sup>のクラスター係数は<math>\textstyle C=\frac{3(a-1)}{2(2a-1)}</math>、平均頂点間距離は<math>\textstyle L=\sqrt[d]{n}/a</math> |
| − | 2/( | + | |
| + | ===木=== | ||
| + | 全頂点が同じ次数を持つ木を考える。中心の頂点<math>v_0</math>を根(root)と呼ぶ。木は定義からサイクルを持たないので<math>C=0</math>。平均頂点間距離は | ||
| + | :<math>n = 1 + d + d(d-1) + ... + d(d-1)^L = 1 +d (1-(d-1)^{L+1})/(1-(d-1))</math>∝<math>(d-1)^{L+1}</math> | ||
| + | を用いて | ||
| + | :<math>\textstyle L=\propto \frac{\log n}{\log (d-1)} \propto \log n</math> | ||
| + | |||
| + | =Erdős–Rényiグラフ= | ||
| + | 各頂点間(全部で<math>n(n-1)/2</math>箇所)に固定した確率<math>p</math>で独立に辺を作成したランダムグラフをErdős–Rényiグラフと呼ぶ。辺確率は独立なので<math>C=p</math>。 | ||
Revision as of 23:05, 6 May 2009
ここでは頂点がすべて連結した無向グラフを扱う。
Contents |
歴史
- 1998 D. J. Watts, Steven Strogatz "Collective dynamics of 'small-world' networks". Nature 393: 440–442. doi:10.1038/30918.
クラスター係数と平均頂点間距離
Link Analysisではグラフにおける各頂点の尺度としてcentralityとprestigeを紹介した。ここではネットワーク全体についての尺度としてクラスター係数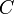
と平均頂点間距離
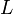を紹介する。
クラスター係数
クラスター係数は隣接する頂点間の辺の密度の平均値にあたる。まず各頂点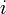
におけるクラスター係数を以下のように定義する。辺の長さはすべて1とする
。
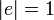グラフ全体のクラスター係数はその平均値になる。
平均頂点間距離
平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点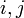
間の最短経路を
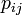と書く。距離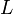以内にある頂点の数を数えることで求められる。
様々なグラフ
完全グラフ
全ての頂点間に辺を持つグラフは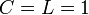
。
格子
平面の場合は三角格子、正方格子が考えられる。特に、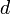
次元空間において辺の長さが単位距離の格子をZdと書く。
- 例. Z2において、
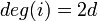
クラスター係数は定義のままだと0になって面白くないので、最短距離が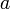
以下の点には全て辺を持つZ'dを考えよう。
- 例. Z'dのクラスター係数は
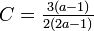、平均頂点間距離は![\textstyle L=\sqrt[d]{n}/a](/mediawiki/images/math/f/5/8/f583b41db535b1a73d0d831b87ea2808.png)
木
全頂点が同じ次数を持つ木を考える。中心の頂点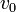
を根(root)と呼ぶ。木は定義からサイクルを持たないので
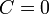。平均頂点間距離は
∝
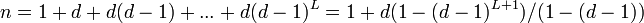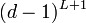
を用いて
Erdős–Rényiグラフ
各頂点間(全部で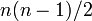
箇所)に固定した確率
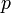で独立に辺を作成したランダムグラフをErdős–Rényiグラフと呼ぶ。辺確率は独立なので
。
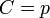