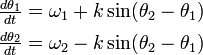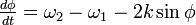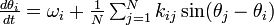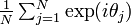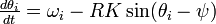Aritalab:Lecture/NetworkBiology/Coupled Oscillator
Contents |
結合振動子
自然振動にばらつきのある素子が相互作用する系を考えましょう。 この分野で最も重要な貢献をした統計物理学者が 蔵本由紀 です。 同期のしやすさはネットワークの形状によりますが、ここでは最も簡単な場合として2個の振動子を考えます。
2つの振動子
振動子の振る舞いは以下の式で記述されます。
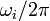 は i に固有の周波数です。また
は i に固有の周波数です。また 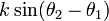 の部分は振動子どうしの引き込み項に対応し、位相の大きさによって周波数に影響を与えます。k が相互作用の強さです。
周波数の差分
の部分は振動子どうしの引き込み項に対応し、位相の大きさによって周波数に影響を与えます。k が相互作用の強さです。
周波数の差分 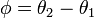 が
が 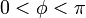 のとき(つまり振動子2が1より前にいるとき)は振動子1が加速して振動子2が減速し、逆に差分が
のとき(つまり振動子2が1より前にいるとき)は振動子1が加速して振動子2が減速し、逆に差分が 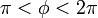 のときは振動子1が減速して振動子2が加速します。
のときは振動子1が減速して振動子2が加速します。
相互作用のパラメータ k (>0) が十分に大きければ振動子は同期、つまり共通の振動数をとって 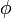 が安定します。
もし
が安定します。
もし 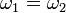 であれば k = 0 でも同期するため、一般性を失わずに
であれば k = 0 でも同期するため、一般性を失わずに 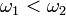 と仮定して、上式の差分を考えましょう。
と仮定して、上式の差分を考えましょう。
定常状態では 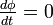 だから
だから
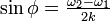 、つまり
、つまり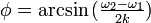 (
(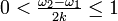 )
)
値 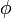 付近の振動子の振る舞いをみましょう。
関数
付近の振動子の振る舞いをみましょう。
関数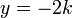
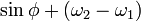 は正の y 切片を持ち
は正の y 切片を持ち 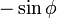 の波形を描きながら
の波形を描きながら 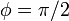 において極小値
において極小値 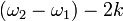 をとり、
をとり、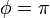 において正の値に戻ります。よって k の値によって以下の場合があります。
において正の値に戻ります。よって k の値によって以下の場合があります。
- k が大きく極小値が負の場合: 解を2つ持つ。そのうち
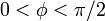 となるほうは振動子2が振動子1の前にある状態で、安定解となる。もう片方は不安定解になる。
となるほうは振動子2が振動子1の前にある状態で、安定解となる。もう片方は不安定解になる。
- k が適切な値で極小値が0の場合: 解を1つ持つ。この値は不安定解になる。
- k が0に近く、極小値が正の場合: 解を持たない。つまり定常状態が存在しない。
結論として、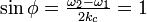 を満たす臨界値
を満たす臨界値 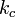 が存在し、この値より k が大きい場合は安定解
が存在し、この値より k が大きい場合は安定解 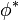 が存在します。
それと等しいか、小さい場合は安定解が存在せず、二つの振動子が同期することはありません。
が存在します。
それと等しいか、小さい場合は安定解が存在せず、二つの振動子が同期することはありません。
N個の振動子
振動子が N 個の場合は
結合する振動子どうしは 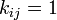 それ以外は 0 とします。
全ての振動子が同数だけ ( K とします) 結合するグラフの場合、
それ以外は 0 とします。
全ての振動子が同数だけ ( K とします) 結合するグラフの場合、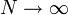 の極限において解くことができます(蔵本モデル)。
の極限において解くことができます(蔵本モデル)。
基本的なアイデアとして、集団としての振幅と位相をそれぞれ R (定数), ψ とおいて平均化した近似を考えます(R = 定数)。N 個の振動子を円周上を回る点と考えた際の重心にあたる値です。
このとき、振動子集団は見かけ上
と簡略化でき、定常状態では 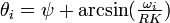 です。R の大きさによって同期するか否かが判断できます。
です。R の大きさによって同期するか否かが判断できます。
- R = 1: 振動子全体が完全に同期している
- R = 0: 振動子が完全にランダム
ネットワーク上の振動子
ネットワーク上に振動子がある場合、基本的には数値シミュレーションによって解析が行われています。 主な成果に以下があります。
- L が大きく、局所的なつながりしかないネットワークは同期しにくい
- ハブがあると同期しやすい
- 参考
- ↑ 指数が虚数である指数関数の定義は
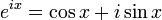 である。
である。