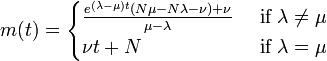Aritalab:Lecture/NetworkBiology/BirthDeath/Continuous
Contents |
出生死亡過程の一般形
確率過程における状態変化を ΔX(t) で表します。つまり
- ΔX(t) = X (t + Δt) - X (t)
一般的な記法では X (t) = i のとき、出生率と死亡率はそれぞれ
- λi (出生), μi (死亡)
で表します。非常に短い時間 Δt の間には、人数 i は一人生まれて i + 1 になるか、一人死んで i − 1 になるはずです。これを数式で書くと増減分を j で表して
と書けます。この式を用いると、時刻 t から t + Δt の間に人口が i から j まで変化する確率は
と展開できます。
j = 0 のとき人口はマイナスにならないため j − 1 という状態は考えません。また μ0 = 0 ですから
と簡略化されます。
j = N という人口の最大値が存在する場合、j + 1 という状態は考えません。また λN = 0 ですから
となります。
コルモゴロフの微分方程式
Eq.1 - 3 から 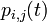 を引いて Δ t で割りましょう。
を引いて Δ t で割りましょう。
この関係は 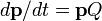 という行列表記に書けます。p は各状態における存在確率です。
という行列表記に書けます。p は各状態における存在確率です。
この過程は、状態 0, 1, 2, ... N の間を動き、λ0 > 0 、μN > 0 なら状態 0, N が反射壁のランダムウォークとみなせます。人口が増える確率は 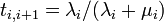 、減る確率は
、減る確率は 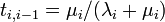 です。遷移行列 T は以下になります。
です。遷移行列 T は以下になります。
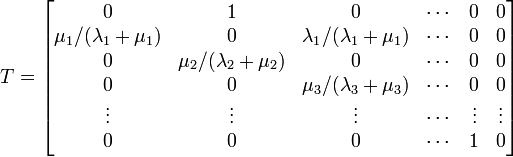
定常分布
生成行列がQで表される連続時間マルコフ連鎖の定常分布 π は
で表されます。
定常分布の一意性
Eq.1 で遷移が定義される連続時間出生死亡過程は、状態数が無限のとき、以下の条件で定常状態 π が一つに定まります。
このとき定常分布は
証明
定常分布が満たす式 π Q = 0 を直接解けばよい。
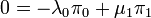 から
から 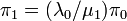
が導かれる。更に、
これを繰り返せば数学的帰納法によって
状態数が無限大の場合は
ただし
の成立が必要で、これは出生率が死亡率よりも少ないことを意味します。
λ と μ が定数の場合
全ての状態において λ, μ が固定値の場合、定常分布は
となります(幾何分布)。人口が発散しないためには λ < μ であることが重要です。定常分布の平均値が平均人口にあたります。
人口の増加率 (λ) で平均人口を割れば平均寿命になります。
様々な出生死亡過程
死亡率 μ が 0 の場合を純出生過程と呼びます。 出生率 λ が 0 の場合を純死亡過程と呼びます。 様々な場合に対して考えてみます。
ポアソン過程 λi =λ, μ = 0
人数に関係なく出生数 λ が一定の場合を考えます。(それぞれの個体はだんだん子供を産まなくなる。)
コルモゴロフの微分方程式は
X(0) = 0 とします。時刻 0 で状態 0 の確率が 1 なので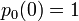 。これを解いて
。これを解いて 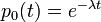
ここから順次計算して
すなわちポアソン分布になります。ポアソン分布の平均と分散は以下になります。
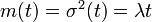
Yule過程: λi = iλ, μ = 0
出生数が人口に比例する場合を考えます。 最初は 1 からスタートし X(0) = 1 とします。
コルモゴロフの微分方程式は
ここから順次計算して
すなわち幾何分布になります。平均と分散は
平均と分散は指数的に増大します。幾何分布になるのは初期値 X(0) = 1 としているためで、これを N に一般化すると負の二項分布になります。
純死亡過程: λ = 0, μi = i μ
死亡数が人口に比例する場合を考えます。 最初は N からスタートし X(0) = N とします。
コルモゴロフの微分方程式は
これを解くと二項分布になります。
平均と分散は以下になります。
平均と分散はともに指数的に減少します。
出生死亡過程: λi = i λ, μi = i μ
コルモゴロフの微分方程式は
計算は大変そうですがこれを解くと
無限時間過ぎた後を考えると
平均と分散は以下になります。
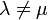 のとき
のとき
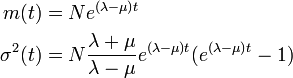
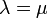 のとき
のとき
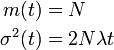
移入のある過程: λi = i λ + ν, μi = i μ
コルモゴロフの微分方程式は
これも頑張ると解けて平均が以下になります。
つまり 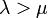 であれば指数的に増加し、等しい時は線形に増加します。しかし
であれば指数的に増加し、等しい時は線形に増加します。しかし 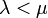 の場合は最終的に
の場合は最終的に 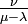 に落ち込みます。
に落ち込みます。
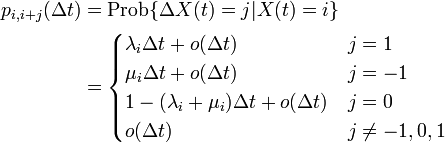
![\begin{align}
Eq.1: p_{i,j}(t + \Delta t) &= p_{i,j-1}(t) \lambda_{j-1} \Delta t \\
&+ p_{i,j+1}(t) \mu_{j+1} \Delta t \\
&+ p_{i,j}(t) [1 - (\lambda_j + \mu_j)\Delta t] + o(\Delta t)
\end{align}](/mediawiki/images/math/a/b/6/ab6aa31623763f5e6ffb59f0a3d03ff5.png)
![\textstyle
Eq.2: p_{i,0}(t + \Delta t) = p_{i,1}(t) \mu_{1} \Delta t + p_{i,0}(t) [1 - \lambda_0 \Delta t] + o(\Delta t)](/mediawiki/images/math/c/3/1/c3113ec0a0dece801b394cefb4d35ae9.png)
![\textstyle
Eq.3: p_{i,N}(t + \Delta t) = p_{i,N-1}(t) \lambda_{N-1} \Delta t + p_{i,N}(t) [1 - \mu_N \Delta t] + o(\Delta t)](/mediawiki/images/math/d/4/9/d49732e89d3bed27819fc7bc3f649c23.png)
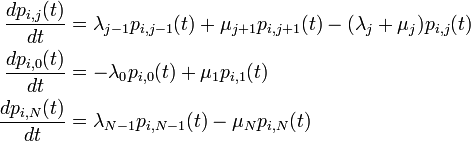
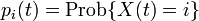
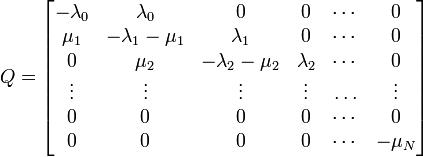
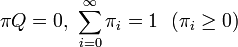
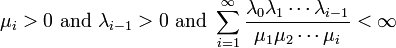
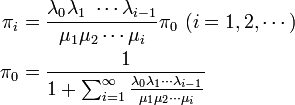
![\begin{align}
\mu_2\pi_2 &= (\lambda_1 + \mu_1) \pi_1 - \lambda_0\pi_0 \\
&= \Big[ \frac{(\lambda_1 + \mu_1)\lambda_0}{\mu_1} - \lambda_0 \Big]\pi_0 \\
\pi_2 &= \frac{\lambda_0\lambda_1}{\mu_1\mu_2} \pi_0
\end{align}](/mediawiki/images/math/2/2/c/22cc0b77f9b4e025ba7fa24e18e757ae.png)
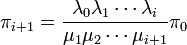
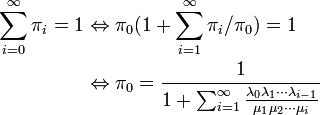
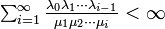

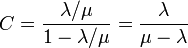
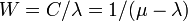
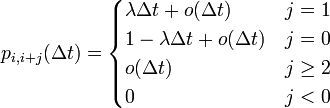
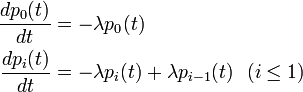
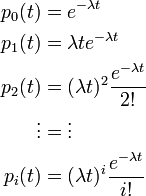
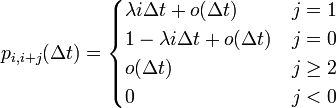
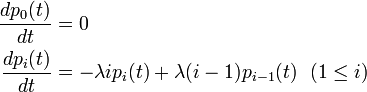
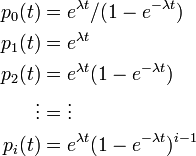
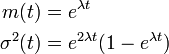
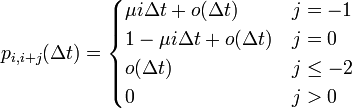
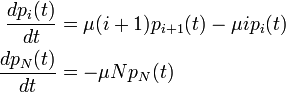
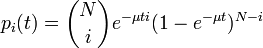
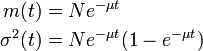
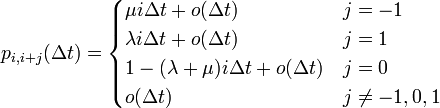
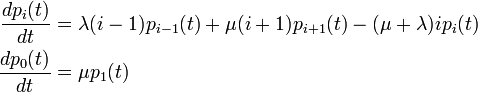
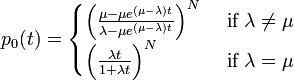
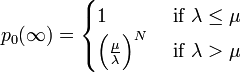
![\begin{align}
p_{i,i+j}(\Delta t) &=
\begin{cases}
\mu i \Delta t + o(\Delta t) & j = -1\\
(\nu + \lambda i) \Delta t + o(\Delta t) & j = 1\\
1 - [\nu + (\lambda + \mu) i ]\Delta t + o(\Delta t) & j = 0 \\
o(\Delta t) & j \neq -1, 0, 1\\
\end{cases}
\end{align}](/mediawiki/images/math/4/3/e/43e936ea09d0f7d5db0023658335bd97.png)
![\begin{align}
\frac{d p_i(t)}{dt} &= [\lambda(i-1) + \nu] p_{i-1}(t) + \mu (i+1) p_{i+1}(t) - (\mu i + \lambda i + \nu) p_i(t)\\
\frac{d p_0(t)}{dt} &= - \nu p_0(t) + \mu p_1(t)
\end{align}](/mediawiki/images/math/5/9/5/595b12d698e30c1dc08174bfea9f2f63.png)