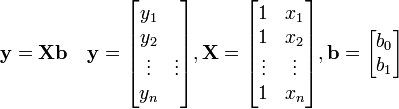Aritalab:Lecture/Math/LR

Revision as of 10:36, 4 June 2013

回帰分析

回帰分析には 1 変量の単回帰 (univariate linear regression) と多変量の重回帰 (multivariate linear regression) があります。モデルしたい変量を y (目的変量）、説明に使う変量を x 、係数を b で表します（ b₀ は定数項）。

(重)回帰モデル 

y = b₀ + x₁ b₁ + x₂ b₂ + ... + x_n b_n　（つまり y を複数の変量 x₁～x_n の線形結合でモデルするやり方）

特に 1 変数の場合を単回帰モデルといいます。

最小二乗法

ここでは最適パラメータを求める最小二乗法を単回帰を使って説明します。

y₁ = b₀ + x₁ b₁ + r₁

y₂ = b₀ + x₂ b₁ + r₂

 :  :

y_n = b₀ + x_n b₁ + r_n

というデータがあると仮定しましょう。y と x が与えられ、ここで決めたいのは最適な b₀, b₁ の値です。r は残差 (residual) といって、y と b₀ + x₁b₁ との差を表します。 最小二乗法とは残差の二乗和 S を最小化するアプローチです。

S = Σ_i f_i²

S の最小値を満たす b₀ と b₁ を求めるには、S を b₀ と b₁ のそれぞれで偏微分して 0 とおいた連立方程式を解けばOKです。つまり

y₁ = b₀ + x₁ b₁

y₂ = b₀ + x₂ b₁

 :  :

y_n = b₀ + x_n b₁

を満たすことになります。これを行列の形に書くと

これから逆行列を用いて b を表せば

b = (X^TX)^-1X^Ty

となります。重回帰の場合も同じ式になります（行列 X の列数が増えるだけ）。 与えられた y, x からこの式を計算するだけで自動的に b の値が求まるのです。

R による実習ページ

行列のランク落ち

線形代数における行列のランク落ちとは、線形独立な変数の数が次数より少ない状態を指します。 回帰分析でいうと、説明変数間に非常に相関が高いものがある場合です（共線性といいます）。 このとき、逆行列の計算も上手くいかず、 b の値がおかしい場合があります。