Aritalab:Lecture/Bioinformatics/Lotka
(Created page with "==ロトカ・ヴォルテラ方程式== ロトカ・ヴォルテラ (Lotka-Volterra) 方程式は、被食者 (prey) ・捕食者 (predator) の関係を表す代表例で...") |
m |
||
| Line 23: | Line 23: | ||
===リアプノフ関数=== | ===リアプノフ関数=== | ||
| − | + | 回転する軌道で保存される量を考えてみます。(a , b) に依存する恒等式として | |
:<math>(\frac{a}{x} - 1) \frac{dx}{dt} + (\frac{b}{y} - 1) \frac{dy}{dt} = 0</math> | :<math>(\frac{a}{x} - 1) \frac{dx}{dt} + (\frac{b}{y} - 1) \frac{dy}{dt} = 0</math> | ||
| − | + | が成立します。つまり微分してこの値になる式は x , y に依存しません。 | |
| − | :<math>\frac{d}{dt}[ a\log x - x + b \log y - y] = 0</math> | + | :<math>\frac{dH(x,y)}{dt} = \frac{d}{dt}[ a\log x - x + b \log y - y] = 0</math> |
| − | + | :<math>H(x,y) = a\log x - x + b\log y - y = const. | |
| − | Hを x で微分すると (a/x - 1), 二階微分は - a / x<sup>2</sup> なので x は a で最大値をとります。同様に y は b | + | Hを x で微分すると (a/x - 1), 二階微分は - a / x<sup>2</sup> なので x は a で最大値をとります。同様に y は b で最大値をとります。つまり H は (a , b) を中心に - ∞ まで減少し、その等高線は閉曲線を成します。つまり軌道は周期的です。 |
| + | |||
このように、平衡点の安定性を示すのに使う関数をリアプノフ関数と呼びます。 | このように、平衡点の安定性を示すのに使う関数をリアプノフ関数と呼びます。 | ||
<ref>リアプノフ関数は全ての平衡点について必ず見つかるわけでもなく、特に決まった定義はありません。</ref> | <ref>リアプノフ関数は全ての平衡点について必ず見つかるわけでもなく、特に決まった定義はありません。</ref> | ||
| Line 46: | Line 47: | ||
\frac{dy}{dt} &= y (-a + x - fy) | \frac{dy}{dt} &= y (-a + x - fy) | ||
\end{align}</math> | \end{align}</math> | ||
| + | ここでは −ex , −fy という項を追加しました。 | ||
| + | このとき <math> dx/dt = 0 , dy/dt = 0 </math> となるのはそれぞれ <math> y = -ex + b, fy = x - a </math> という直線になります。 | ||
| − | + | 二本の直線はy切片がそれぞれ正と負です。第一象限で交わる場合もあるし、そうでない場合もあるので、まず交わる場合を考えます。 | |
| − | + | {| class="wikitable" align="center" | |
| − | + | |+ 直線上の、交点の左右における時間微分値 | |
| + | ! 直線 || dx/dt || dy/dt | ||
| + | |- | ||
| + | | <math> y = -ex + b</math> || 0 || 負 → 交点 → 正 | ||
| + | |- | ||
| + | | <math> fy = x - a</math> || 正 → 交点 → 負 || 0 | ||
| + | |} | ||
| + | 正負の値から、反時計回りに回転することがわかります。ただしこの解析だけからは、交点に収束するのか交点から発散するかはわかりません。 | ||
| − | + | 第一象限で交わらない場合は、第一象限に交点があるときの挙動を切り取った形になっています。x 軸に相当する部分 (y = 0) を考えると <math> y = -ex + b</math> の x 切片 b/e に収束します。 y 軸に相当する部分 (x = 0) を考えると、常に減少です。すなわち、二本の直線が y 座標が負の部分で交わるとき、 (0, b/e) が安定不動点になります。 | |
| − | <math> y = -ex + b</math> の x 切片 b/e に収束します。 y 軸に相当する部分 (x = 0) を考えると、常に減少です。すなわち、二本の直線が y 座標が負の部分で交わるとき、 (0, b/e) | + | |
===リアプノフ関数=== | ===リアプノフ関数=== | ||
| − | + | 交点の周りでの挙動を調べるため、ロトカ・ヴォルテラ方程式と同様のリアプノフ関数を考えてみましょう。 | |
:<math>H(x,y) = u \log x - x + v \log y - y </math> | :<math>H(x,y) = u \log x - x + v \log y - y </math> | ||
| − | + | この関数は二本の直線の交点(x座標は正) | |
:<math>(u , v) = \Big(\frac{a+bf}{ef+1}, \frac{b-a}{ef+1}\Big)</math> | :<math>(u , v) = \Big(\frac{a+bf}{ef+1}, \frac{b-a}{ef+1}\Big)</math> | ||
| − | + | で最大値をとり、そこから離れるほど−∞に近づきます。ここまではロトカ・ヴォルテラ方程式とそう変わりません。 | |
| − | 交点では<math> v = -eu + b, fv = u - a </math> | + | |
| + | 交点では<math> v = -eu + b, fv = u - a </math>が成立するので | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\frac{H(x,y)}{dt} &= \frac{\partial H}{\partial x} \frac{dx}{dt} + | \frac{H(x,y)}{dt} &= \frac{\partial H}{\partial x} \frac{dx}{dt} + | ||
| Line 71: | Line 81: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | つまり H(x,y) は (u , v) においてのみ 0 | + | つまり <math>d H(x,y)/dt</math> は (u , v) においてのみ 0 となり(安定)、それ以外の場合は安定点に向かって上り勾配です。H(x , y) の値と考え合わせると (u , v) は大域安定でもあります。 |
| − | + | 定性的解釈としては、如何に種内競争の項 e や f が小さくても、存在しさえすれば、それらが大域的安定点を作り出すことを示しています。つまり、ロトカ・ヴォルテラ方程式の周期性は構造的に安定ではありません。 | |
==安定性解析== | ==安定性解析== | ||
| − | + | ここで話を一般化します。一般的な微分方程式系を考えましょう。 | |
| − | + | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 84: | Line 93: | ||
\end{align}</math> | \end{align}</math> | ||
| − | 定常状態を (x<sup>*</sup>, y<sup>*</sup>) とし、そこから少しずれた位置の挙動を調べます。それには (x<sup>*</sup> + u, y<sup>*</sup> + v) とした差分 u , v | + | 定常状態を (x<sup>*</sup>, y<sup>*</sup>) とし、そこから少しずれた位置の挙動を調べます。それには (x<sup>*</sup> + u, y<sup>*</sup> + v) とした差分 u , v をテイラー展開します。ずれが微小であることから2次以上の部分は無視します。 |
:<math>\begin{align} | :<math>\begin{align} | ||
| − | \frac{du}{dt} &= f(x^* + u, y^* + v) | + | \frac{du}{dt} &= f(x^* + u, y^* + v) - f(x^*, y^*) = f_x(x^*, y^*)u + f_y(x^*, y^*)v + \cdots \\ |
| − | \frac{dv}{dt} &= g(x^* + u, y^* + v) | + | \frac{dv}{dt} &= g(x^* + u, y^* + v) - g(x^*, y^*) = g_x(x^*, y^*)u + g_y(x^*, y^*)v + \cdots |
\end{align}</math> | \end{align}</math> | ||
| Line 98: | Line 107: | ||
</math> | </math> | ||
| − | 行列 J をヤコビ行列 (Jacobian) | + | 行列 J をヤコビ行列 (Jacobian) といいます。線形微分方程式であれば J の固有値 λ<sub>1</sub>, λ<sub>2</sub> を用いた解があります。 |
: λ<sub>1</sub> ≠ λ<sub>2</sub> のとき | : λ<sub>1</sub> ≠ λ<sub>2</sub> のとき | ||
| Line 112: | Line 121: | ||
</math> | </math> | ||
| − | + | 固有値を実数とすると、λ<sub>1</sub> < 0, λ<sub>2</sub> < 0 であれば、平衡点からのズレ u , v が時間とともに e<sup>λ t</sup> → 0 に収束します。どちらかでも正であれば、ズレは発散します。 | |
固有値が複素数の時、2つの固有値は複素共役になり λ<sub>1</sub>, λ<sub>2</sub> = a ± <i>i</i> b です。虚数の exp は絶対値が 1 になることを利用して | 固有値が複素数の時、2つの固有値は複素共役になり λ<sub>1</sub>, λ<sub>2</sub> = a ± <i>i</i> b です。虚数の exp は絶対値が 1 になることを利用して | ||
:<math>\lim_{t \rightarrow \infty}| \exp(a \pm ib)t | = \lim_{t \rightarrow \infty} \exp(at) \times | \exp(\pm ibt) | = \lim_{t \rightarrow \infty} \exp(at) </math> | :<math>\lim_{t \rightarrow \infty}| \exp(a \pm ib)t | = \lim_{t \rightarrow \infty} \exp(at) \times | \exp(\pm ibt) | = \lim_{t \rightarrow \infty} \exp(at) </math> | ||
| − | + | です。つまり虚数の部分は影響を与えません。固有値の実部が共に負であれば、平衡点からのズレはやはり 0 に収束することがわかります。 | |
| − | + | さらにこの議論は多元連立の場合もそのまま成立します。 | |
まとめると、 | まとめると、 | ||
| Line 127: | Line 136: | ||
==競争方程式== | ==競争方程式== | ||
| − | + | 安定性解析をベースに、被・捕食者系を捉え直してみます。 | |
| − | + | ここで係数の符号が異なる競争系を考えましょう。 | |
:<math>\begin{align} | :<math>\begin{align} | ||
\frac{dx}{dt} &= x (1 - ax - by)\\ | \frac{dx}{dt} &= x (1 - ax - by)\\ | ||
\frac{dy}{dt} &= y (1 - cx - dy) | \frac{dy}{dt} &= y (1 - cx - dy) | ||
\end{align}</math> | \end{align}</math> | ||
| − | + | 種 x と y の相互作用の関係は対称形で、被・捕食者系とは y の単独の増殖率および c の符号が違っています。安定点は | |
:<math>(u , v) = \Big(\frac{d-b}{ad-bc}, \frac{a-c}{ad-bc}\Big)</math> | :<math>(u , v) = \Big(\frac{d-b}{ad-bc}, \frac{a-c}{ad-bc}\Big)</math> | ||
| − | |||
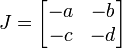
ヤコビ行列は | ヤコビ行列は | ||
| − | :<math>J = \begin{bmatrix} -a | + | :<math>J = \begin{bmatrix} -a & -b \\ -c & -d \end{bmatrix}</math> |
| − | + | です。被・捕食者系と異なり、二本の直線はいずれも傾きが負です。直線どうしは第一象限で交わる場合もあるし、交わらない場合もあります。 | |
| − | 交わる場合から考えます。ad − bc > 0 の場合、交点 (u , v) の分母は正になり、交点が第一象限にあることから d > b > 0, a > c > 0 | + | 交わる場合から考えます。ad − bc > 0 の場合、交点 (u , v) の分母は正になり、交点が第一象限にあることから d > b > 0, a > c > 0 です。さらに ad - bc > 0, (-a + -d) < 0 を満たすので、ヤコビ行列の固有値は負になります。つまり交点は大域安定な不動点です。 |
| − | + | 同じことは dx/dt, dy/dt の符号を考えても (u , v) に近づくのでわかります。 | |
| + | ここまでは被・捕食者系と全く同じです。 | ||
| − | 次に ad − bc < 0 | + | 次に ad − bc < 0 の場合を考えます(被・捕食者系は c の符号が負のため、この場合が生じませんでした)。交点の分母が負になるので b > d > 0, c > a > 0 です。このとき、x 軸上 (y = 0) の切片 1/a および y 軸上 (x = 0) の切片 1/d に収束します。初期条件に依存してどちらかの種が絶滅することがわかります。交点は不安定不動点です。 |
===リアプノフ関数=== | ===リアプノフ関数=== | ||
| Line 163: | Line 172: | ||
</math> | </math> | ||
二次形式の形をとり (u , v) では 0 になっています。 | 二次形式の形をとり (u , v) では 0 になっています。 | ||
| + | |||
<references/> | <references/> | ||
Revision as of 06:45, 18 April 2013
Contents |
ロトカ・ヴォルテラ方程式
ロトカ・ヴォルテラ (Lotka-Volterra) 方程式は、被食者 (prey) ・捕食者 (predator) の関係を表す代表例です。[1] このモデルでは、被食者 x は放っておくと増加し (ax)、捕食者によって減少します (bxy) 。捕食者 y は捕食によって増加し (dxy)、放っておくと減少します (cy)。ここで a, b, c, d は全て正のパラメータです。
これ以降、 x , y を適当なスケーリングによって無次元化しておきます。問題の本質は変わりません。
この解は
これらがxy平面において x > 0, y > 0 象限の境界をなしており、(x , y) の動く範囲を中に包含しています。平衡点は原点および (a , b) です。この点を境に dx/dt, dy/dt の符号が変化します。その符号から x = a, y = b を境に4つのエリアに分割され、半時計方向に回転する軌道の存在がわかります。
リアプノフ関数
回転する軌道で保存される量を考えてみます。(a , b) に依存する恒等式として
が成立します。つまり微分してこの値になる式は x , y に依存しません。
![\frac{dH(x,y)}{dt} = \frac{d}{dt}[ a\log x - x + b \log y - y] = 0](/mediawiki/images/math/6/1/5/6154edd9aa46ef1b32476ebe26003d24.png)
- Failed to parse (lexing error): H(x,y) = a\log x - x + b\log y - y = const. Hを x で微分すると (a/x - 1), 二階微分は - a / x<sup>2</sup> なので x は a で最大値をとります。同様に y は b で最大値をとります。つまり H は (a , b) を中心に - ∞ まで減少し、その等高線は閉曲線を成します。つまり軌道は周期的です。 このように、平衡点の安定性を示すのに使う関数をリアプノフ関数と呼びます。 <ref>リアプノフ関数は全ての平衡点について必ず見つかるわけでもなく、特に決まった定義はありません。</ref> 周期の振幅と振動数は a , b に依存します。平均値を調べてみましょう。ちょっと技巧的ですが log x(t) の時間微分を積分します。 :<math>\begin{align} \frac{1}{T}\int^T_0 \frac{d}{dt} \log x(t) dt &= \frac{1}{T}\int^T_0 \frac{dx}{dt} \frac{d}{dx} \log x(t) dt = \frac{1}{T}\int^T_0 x (b - y) \frac{1}{x} dt \\ \log x(T) - \log x(0) &= 0 = b - \frac{1}{T}\int^T_0 y(t) dt \end{align}
つまり y の時間平均は b です。同様に x の時間平均は a です。
種内競争を持つ被・捕食者系
ロトカ・ヴォルテラ方程式は捕食者がいないと被食者が指数的に増えてしまうので、これをロジスティック式で補正します。
ここでは −ex , −fy という項を追加しました。
このとき 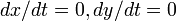 となるのはそれぞれ
となるのはそれぞれ 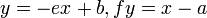 という直線になります。
という直線になります。
二本の直線はy切片がそれぞれ正と負です。第一象限で交わる場合もあるし、そうでない場合もあるので、まず交わる場合を考えます。
| 直線 | dx/dt | dy/dt |
|---|---|---|
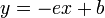 |
0 | 負 → 交点 → 正 |
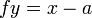 |
正 → 交点 → 負 | 0 |
正負の値から、反時計回りに回転することがわかります。ただしこの解析だけからは、交点に収束するのか交点から発散するかはわかりません。
第一象限で交わらない場合は、第一象限に交点があるときの挙動を切り取った形になっています。x 軸に相当する部分 (y = 0) を考えると 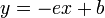 の x 切片 b/e に収束します。 y 軸に相当する部分 (x = 0) を考えると、常に減少です。すなわち、二本の直線が y 座標が負の部分で交わるとき、 (0, b/e) が安定不動点になります。
の x 切片 b/e に収束します。 y 軸に相当する部分 (x = 0) を考えると、常に減少です。すなわち、二本の直線が y 座標が負の部分で交わるとき、 (0, b/e) が安定不動点になります。
リアプノフ関数
交点の周りでの挙動を調べるため、ロトカ・ヴォルテラ方程式と同様のリアプノフ関数を考えてみましょう。
この関数は二本の直線の交点(x座標は正)
で最大値をとり、そこから離れるほど−∞に近づきます。ここまではロトカ・ヴォルテラ方程式とそう変わりません。
交点では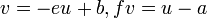 が成立するので
が成立するので
つまり 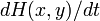 は (u , v) においてのみ 0 となり(安定)、それ以外の場合は安定点に向かって上り勾配です。H(x , y) の値と考え合わせると (u , v) は大域安定でもあります。
は (u , v) においてのみ 0 となり(安定)、それ以外の場合は安定点に向かって上り勾配です。H(x , y) の値と考え合わせると (u , v) は大域安定でもあります。
定性的解釈としては、如何に種内競争の項 e や f が小さくても、存在しさえすれば、それらが大域的安定点を作り出すことを示しています。つまり、ロトカ・ヴォルテラ方程式の周期性は構造的に安定ではありません。
安定性解析
ここで話を一般化します。一般的な微分方程式系を考えましょう。
定常状態を (x*, y*) とし、そこから少しずれた位置の挙動を調べます。それには (x* + u, y* + v) とした差分 u , v をテイラー展開します。ずれが微小であることから2次以上の部分は無視します。
これを行列の形に書くと
行列 J をヤコビ行列 (Jacobian) といいます。線形微分方程式であれば J の固有値 λ1, λ2 を用いた解があります。
- λ1 ≠ λ2 のとき
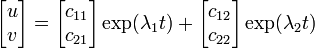
- λ1 = λ2 = λ のとき
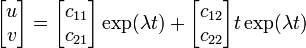
固有値を実数とすると、λ1 < 0, λ2 < 0 であれば、平衡点からのズレ u , v が時間とともに eλ t → 0 に収束します。どちらかでも正であれば、ズレは発散します。 固有値が複素数の時、2つの固有値は複素共役になり λ1, λ2 = a ± i b です。虚数の exp は絶対値が 1 になることを利用して
です。つまり虚数の部分は影響を与えません。固有値の実部が共に負であれば、平衡点からのズレはやはり 0 に収束することがわかります。 さらにこの議論は多元連立の場合もそのまま成立します。
まとめると、
- 固有値の実部が全て負であれば、平衡点は局所安定
- 固有値の実部が一つでも正であれば、平衡点は不安定
となります。固有値が複素数の時は近傍で振動がおこります。
2 x 2 行列 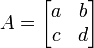 の場合は固有方程式 x2 - (a + d) x + (ad - bc) = 0 の解が固有値です。
固有値実部が負であるための必要十分条件は tr(A) = a + d < 0 かつ det(A) = ad - bc > 0 です。
の場合は固有方程式 x2 - (a + d) x + (ad - bc) = 0 の解が固有値です。
固有値実部が負であるための必要十分条件は tr(A) = a + d < 0 かつ det(A) = ad - bc > 0 です。
競争方程式
安定性解析をベースに、被・捕食者系を捉え直してみます。 ここで係数の符号が異なる競争系を考えましょう。
種 x と y の相互作用の関係は対称形で、被・捕食者系とは y の単独の増殖率および c の符号が違っています。安定点は
ヤコビ行列は
です。被・捕食者系と異なり、二本の直線はいずれも傾きが負です。直線どうしは第一象限で交わる場合もあるし、交わらない場合もあります。
交わる場合から考えます。ad − bc > 0 の場合、交点 (u , v) の分母は正になり、交点が第一象限にあることから d > b > 0, a > c > 0 です。さらに ad - bc > 0, (-a + -d) < 0 を満たすので、ヤコビ行列の固有値は負になります。つまり交点は大域安定な不動点です。 同じことは dx/dt, dy/dt の符号を考えても (u , v) に近づくのでわかります。 ここまでは被・捕食者系と全く同じです。
次に ad − bc < 0 の場合を考えます(被・捕食者系は c の符号が負のため、この場合が生じませんでした)。交点の分母が負になるので b > d > 0, c > a > 0 です。このとき、x 軸上 (y = 0) の切片 1/a および y 軸上 (x = 0) の切片 1/d に収束します。初期条件に依存してどちらかの種が絶滅することがわかります。交点は不安定不動点です。
リアプノフ関数
競争方程式のリアプノフ関数を考えましょう。
二本の直線の交点は
です。
交点では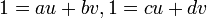 が成立するので
が成立するので
二次形式の形をとり (u , v) では 0 になっています。
- ↑ ロトカは人口モデルのロトカと同一人物で、ヴォルテラ (Vito Volterra) はイタリアの数学者です。それぞれが独立に発見した理論なのでこう呼ばれます。
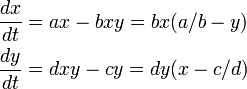
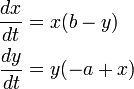
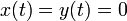
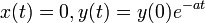
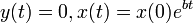
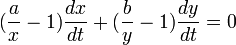
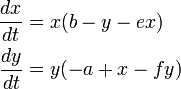
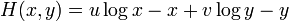
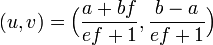
![\begin{align}
\frac{H(x,y)}{dt} &= \frac{\partial H}{\partial x} \frac{dx}{dt} +
\frac{\partial H}{\partial y} \frac{dy}{dt} \\
&= (\frac{u}{x} - 1) \frac{dx}{dt} + (\frac{v}{y} - 1) \frac{dy}{dt} \\
&= (\frac{u}{x} - 1) x (b - y - ex) + (\frac{v}{y} - 1)y (-a + x - fy)\\
&= (u-x) [(v + eu) - y - ex] + (v - y) [(-u + fv) + x - fy]\\
&= e(u-x)^2 + f(v-y)^2 \geq 0\\
\end{align}](/mediawiki/images/math/a/3/8/a3897c05009161a3488f31d23e49d20b.png)
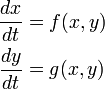
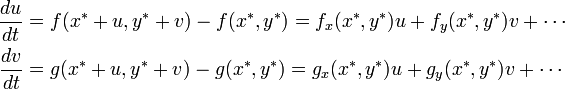
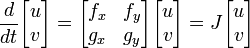
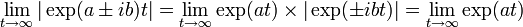
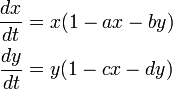
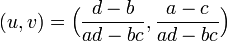
![\begin{align}
\frac{H(x,y)}{dt} &= \frac{\partial H}{\partial x} \frac{dx}{dt} +
\frac{\partial H}{\partial y} \frac{dy}{dt} \\
&= (\frac{u}{x} - 1) \frac{dx}{dt} + (\frac{v}{y} - 1) \frac{dy}{dt} \\
&= (\frac{u}{x} - 1) x (1-ax-by) + (\frac{v}{y} - 1)y (1-cx-dy)\\
&= (u-x) [a(u-x) +b(v-y)] + (v - y) [c(u-x)+d(v-y)]\\
&= a(u-x)^2 + (b+c)(u-x)(v-y) + d(v-y)^2\\
\end{align}](/mediawiki/images/math/a/8/5/a8562f9945c474596f852c1e7dac7a18.png)