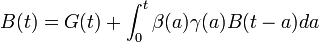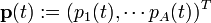Aritalab:Lecture/Bioinformatics/Logistic
m (→ロジスティックモデル) |
m (→基本モデルの歴史) |
||
| Line 1: | Line 1: | ||
| − | == | + | ==1変数基本モデルの歴史== |
数理生物学は、マクロからミクロまでの様々な生命現象を数学的にモデルし解釈する分野です。手法の多くは微分方程式や離散系などの力学系 (dynamical system) を用い、時間や空間に沿った状態変化を解析します。歴史的にみると、数理生物学は人口の数理モデルに端を発しています。 | 数理生物学は、マクロからミクロまでの様々な生命現象を数学的にモデルし解釈する分野です。手法の多くは微分方程式や離散系などの力学系 (dynamical system) を用い、時間や空間に沿った状態変化を解析します。歴史的にみると、数理生物学は人口の数理モデルに端を発しています。 | ||
Revision as of 00:34, 9 April 2013
Contents |
1変数基本モデルの歴史
数理生物学は、マクロからミクロまでの様々な生命現象を数学的にモデルし解釈する分野です。手法の多くは微分方程式や離散系などの力学系 (dynamical system) を用い、時間や空間に沿った状態変化を解析します。歴史的にみると、数理生物学は人口の数理モデルに端を発しています。
マルサスモデル
人口は集団サイズが大きいので連続量として表現でき、古くから解析の対象でした。資源に制約がない居住環境では、時刻 t における人口を P(t) としてその成長を以下のように書けるでしょう。
ここで λ は人口の成長率で出生率から死亡率を引いたものにあたります。これを解けば
となり指数関数的に増加します。これをマルサス型の人口モデル (Malthusian population model) といいます。[1]
この人口モデルを離散時間に対して作れば
となり、これを解くと
になります。連続モデルと離散モデルはそう違わないといえるでしょう。これから P(t) の代わりに x を用います。明示的には書きませんが、時間依存の関数であることに注意してください。
ロジスティックモデル
19世紀に入ると、フェアハルスト (Pierre F Verhulst) は上限のある人口増加を定式化しました。
マルサス型の増加 xr と密度効果 (1 - x/K) をかけた形になっています。この式では成長率が定数ではなく一定値 K (>0) に単調に近づきます。この K を環境容量 (carrying capacity) と呼びます。つまり資源の上限に近づくと増加率に負の効果を与えます(ロジスティック効果)。この理由で、これをロジスティックモデルと呼びます。 これを解くと
になります。ここで x0 は初期値(定数)です。上限 K に漸近することがよくわかります。この形状はシグモイドとも呼ばれます。実際の人口増加はモデルできないことが知られていますが、微生物の細胞数などにはよく当てはまります。
ロジスティック式において x = 0 と x = K は個体数が変化しない平衡状態 (equilibrium) にあたります。このうち x = K はそこからずれても元に戻る安定点 (stable point)、x = 0 は不安定点です。
局所安定と大域安定
平衡から少しずらしても元に戻る平衡点を局所安定点と呼びます。局所安定な平衡点は一つとは限らないので、収束先は初期値に依存します。もし、初期条件に関わらず収束する安定点がある場合、それを大域安定な平衡点と呼びます。
ロジスティック式の場合、x = K は大域安定点になっています。
変数分離法
非線形の微分方程式は常に解けるとは限らないのですが、ロジスティック式は変数分離法を使って解けます。 まず式を変形します。
それから積分します。
ここで初期条件 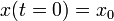 を使うと上記の式が得られます。
を使うと上記の式が得られます。
リッカーモデル
このモデルの離散時間版はカオスを含むとても複雑な挙動を取ります。
また離散時間のモデルで密度の効果が指数的に効くものをリッカー (Ricker) モデルといいます。
この一次近似をとると ![\exp \Big[ r \Big( 1 - \frac{x_t}{K} \Big) \Big] = 1 + r \Big(1 - \frac{x_t}{K} \Big)](/mediawiki/images/math/7/f/9/7f95c7624007cbeb27f72e061987d575.png) になるのでロジスティック式になっています。
になるのでロジスティック式になっています。
安定人口モデル
20世紀になると、年齢別の出生率を考慮したモデルがロトカ (Alfred Lotka) などにより研究されました。ロトカはアメリカの統計学者で20世紀初頭に活躍した人です。
上式で B(t) は単位時間あたりの出生数、β は年齢別の出生率、γ は a 歳までの生存率、G(t) は時刻 0 における初期人口による出生数になります。これを安定人口モデル (stable population model) と呼びます。
レスリー行列
安定人口モデルの離散版は行列を用いて表現できます。年齢を A グループに分け、A x A 行列で単位時間あたりの人口遷移を表現します。
この行列を考案者 Patrick Leslie の名前をとってレスリー行列と呼びます。 最初の行は各年齢グループによる単位時間あたりの出生数で、次行から下の pi は年齢 i の個体が単位時間生存して i+1 になる確率です。時刻 t における年齢 i の人口を pi と書いた人口ベクトルを
とすると単位時間後の人口は 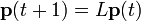 と表されます。時間 t 後の人口は
と表されます。時間 t 後の人口は 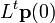 となります。
このモデルでは、全個体数に対する各年齢の割合が時間が経つにつれて一定に落ち着きます。また個体数の増加率も一定値 λ に落ち着き、この値はレスリー行列の最大固有値です。[2]
となります。
このモデルでは、全個体数に対する各年齢の割合が時間が経つにつれて一定に落ち着きます。また個体数の増加率も一定値 λ に落ち着き、この値はレスリー行列の最大固有値です。[2]
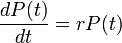
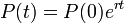
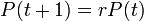
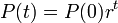
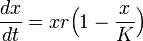
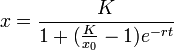
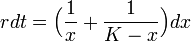
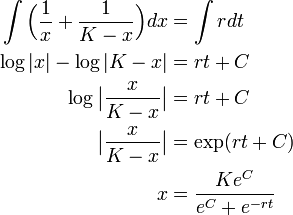
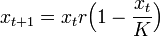
![x_{t+1} = x_t \exp \Big[ r \Big( 1 - \frac{x_t}{K} \Big) \Big]](/mediawiki/images/math/0/1/8/0185c3b3c17352a8753845d1822b644d.png)