Aritalab:Lecture/Automata/ContextFree
m (→uvwxy定理) |
m |
||
| Line 2: | Line 2: | ||
|__TOC__ | |__TOC__ | ||
|} | |} | ||
| − | == | + | [[Aritalab:Lecture/Automata|形式言語理論のトップページヘ]] |
| + | ==まとめ== | ||
文脈自由文法では正則表現よりも複雑な言語に属する列を生成できます。 | 文脈自由文法では正則表現よりも複雑な言語に属する列を生成できます。 | ||
文脈自由文法は書換え規則の集合として表現され、 | 文脈自由文法は書換え規則の集合として表現され、 | ||
Latest revision as of 12:04, 7 May 2012
|
[edit] まとめ
文脈自由文法では正則表現よりも複雑な言語に属する列を生成できます。 文脈自由文法は書換え規則の集合として表現され、 殆んどのプログラミング言語は文脈自由言語で記述されます。 例えば四則演算の式は以下のように表現できます。記号 | は「または」の意味、NUMBER は任意の正の数を表しています。
expr = expr + expr
| expr - expr
| expr * expr
| expr / expr
| (expr)
| - expr
| NUMBER
式の中にはカッコ()の対応が出てくるので、四則演算の式は正則表現で表現できないことに注意しましょう。 文脈自由文法をオートマトンでシミュレートするにはより複雑な構造が必要です。 正則表現が有限オートマトンと等価であったように、文脈自由文法はプッシュダウンオートマトン(スタックを備えたオートマトン)と等価なことがわかっています。
[edit] 文脈自由文法
文脈自由文法 (CFG: context-free grammar) は G = (V, Σ, P, S) の組で与えられます。V, Σ, P はそれぞれ変数、終端記号、生成規則の有限集合で、S ∈ V は開始記号です。 生成規則は変数 A と列 α ∈ (V ∪ Σ)* に対して、A → α という形をとります。 つまり、常に1 つの変数をある文字列に展開していく文法です。 普通は変数を大文字、終端記号を小文字または数字で書きます。 非決定性オートマトンのように、ある時点で適用可能な規則は複数あっても大丈夫です。 生成規則により列を生成する過程を導出といいます。 より形式的には、2 つの列 u, v ∈ (V ∪ Σ)* に対して共通の接尾辞 α, γ ∈ (V ∪ Σ)* と生成規則 A → β ∈ P が存在して
- u = α A γ
- v = α β γ
と書けるとき、v は u から1ステップで導出されると呼びます。 文法 G の開始記号を S としたとき、変数を含まない列 x ∈ Σ* が S から導出されるとき、 x は文法 G によって生成されるといいます。 生成される列の全体を文法 G が生成する言語と呼び、L(G) と書きます。 生成規則 A → α と A → β があるとき、簡略化して A → α | β と書きます。
- L(G) = { 0n1n | n ≥ 0 } はCFGで書ける
G = ( {S}, {0,1}, {S → ε | 0S1 }) とすれば
- S ⇒ 0S1 ⇒ 00S11 ...
となります。
- L(G) = { z zR | z ∈ {0,1}* } はCFGで書ける
G = ( {S}, {0,1}, {S → ε | 0S0 | 1S1 }) とすれば 任意のzzRを生成できます。
- L(G) = { z zR | z ∈ {0,1}* } の補集合 L' = {0,1}* - L(G) はCFGで書ける
求めたい文法は、長さが奇数となる文字列か、列の両端から等距離にある位置に異なる記号がでてくる言語です。長さが奇数になる列は以下のようになります。
- S1 → 0 | 1 | 00S1 | 01S1 | 10S1 | 11S1
列の両端から等距離にある位置に異なる記号が現れる列は
- α0β1αR, α1β0αR
の形で記述できます。よってこれを生成する文法は真ん中のβを生成する変数をBとして
- S2 → 0S20 | 1S21 | 0B1 | 1B0
- B → 0B | 1B | ε
と書けます。最後に二つの文法をあわせて
- S → S1 | S2
とすれば文法が完成です。 この例から、言語 L1 と L2 がCFGで生成されるなら、それらの和集合もCFGで生成できることがわかります。
[edit] 最左導出
CFGの定義ではある時点で適用可能なルールが複数あっても大丈夫です。 しかしこれでは、ある列 x と文法 G を与えられて G が x を導出するかどうかを見極めるのが難しくなります。 この判断をより簡単にするため、CFGに導出のルールを定めます。 最左導出とは、生成規則を適用する際に常に最も左の変数に規則を適用するという制限のことです。 この制限をつけても、文法 G が生成する(終端記号だけからなる)文字列なら全て(最左導出で)導出できます。 生成規則は常に変数を1個だけ変換します。従って、変換の順番は最終的に生成される列 に影響を与えません。よって変換の順番をうまく並び替えることにより、最左導出を与えることができるのです。文脈自由という言葉の由来は、変数1個だけを変換し、隣にある変数や終端記号に影響されないことからきています。
[edit] DFA ⊂ CFG
任意の正則言語 L に対して、それを生成するCFGを構成できます。 L はDFAと等価であるため、認識するオートマトンが存在します。 その各遷移規則 Si--(a)-->Sjに対して、CFGの生成規則 Si = aSj を作成すればCFGになります。Sjが受理状態の場合は Si = a とします。
[edit] グライバッハ標準形
CFGでは同じ文法を様々な形に記述できます。 まず、チョムスキー標準形があります。 これは、「生成規則の右辺をただ一個の終端記号か二個の変数のみに限定する」というものです。つまり、常に列の記号数を増やす方向か、終端記号に置き換える方向にしか規則を適用しません。直感的には分かりやすいですが理論的な応用先はありません。 これに対しグライバッハ標準形は、「適用規則の右辺が左端に 1 個の終端記号と 0 個以上の変数からなる」というもので、CFGの特徴をつかむのに役立ちます。 例えば、グライバッハ標準形では各規則が 1 個の終端記号を含むため、長さ n の列を導出する際に規則の適用回数は n 回です。
どんなCFGにもグライバッハ標準形が存在します。 右辺の先頭が変数で始まる規則 R に対し、他の規則を使って置き換えられるパターンを全て尽くしてゆけば最後は終端記号になるはずなので、それまでの変換全てを 1 個の規則とみなしてもとの規則 R を取り除きます。 ただし、S → SA | 0, A → 1 のような文法だと S ⇒ SAAAA ... となってしまい、どの段階で S を 0 にするかがわかりません。 この場合、A の繰り返しを表現する新しい変数を導入します。
- S → 0 | 0B, B → A | AB
となっていれば
- S → 0 | 0B, B → A | 1B
と置き換えることができます。
[edit] uvwxy定理
L を有限でない CFG とします。すると L によって決まる定数 K が存在し、L に属し、長さが K 以上の任意の列 z について以下の3条件が成り立ちます。 ただしこれは必要条件であり、十分条件ではありません。
- z= uvwxy
- vx ≠ ε
- 任意の i に対し、uviwxiy ∈ L
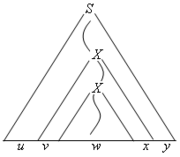
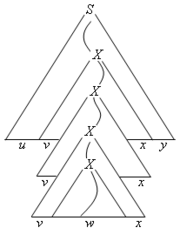
まず、L をグライバッハ標準形になおし、生成規則として右辺が1個の変数だけのものが無いと仮定しましょう。そして、十分に長い列の導出木を考えます。 文脈自由言語 L は無限集合なので、そのような木は必ず存在します。 導出木の最長パスの長さ n が文法に現われる変数の総数を上回るとき、同一の変数 X がそのパス上に 2 回以上現われているはずです。 そこで、最後に現われた X より下の導出を w、最初に現われた X より左と右の部分の導出をそれぞれ u,y とおきます (図1)。 生成規則には右辺が変数1個だけのものは存在しませんから、v, x の部分は少なくとも片方が ε ではありません。 更に、最後に現われた x の部分以降の導出を、それ以前に現われた x の導出と置き換えることにより、uviwxiy の列を導出できます (図2)。 この定理はポンピング補題とも呼ばれ、正則言語にも対応する補題があります。
- L = { 0n1n0n | n ≥ 1 } はCFGで書けない
0n1n0n がCFGで書けると仮定して、 0n1n0n = uvwxy という分解を考えます。 このとき uviwxiy も L に含まれるはずですが、 v, x の2箇所の繰り返しでは、a,b,c の3つの繰り返しを表現できないので矛盾します。
- L = { zz | z ∈ {0,1}* } はCFGで書けない
zz は u=w=y=εとおけば uvwxy で表現できるように思えますが、上の定理は十分条件ではありません。例えば z = 0n1n とおくと、L は 0n1n0n1n という列を含みますが、これはCFGで書けません。
- L = { zzR | z ∈ {0,1}* } はCFGで書ける
これはプッシュダウンオートマトンを理解するとわかります。