Aritalab:Lecture/Algorithm/Reducibility
m (→三次元マッチング) |
m (→三次元マッチング) |
||
| Line 52: | Line 52: | ||
と定義します。3SATに出現する変数に対応する真偽値設定用の要素は 2nm 個あります。そのうち、真偽値設定モジュールで半数を利用するので、残りは nm 個です。そのうち、充足性判定用に各節から 1 つずつ、合計 m 個の要素を使います。残った m(n−1) 個をガーベッジコレクションするので、 g<sub>1</sub>[k], g<sub>2</sub>[k]を 1 ≤ k ≤ m(n−1) 個用意し、それぞれについて、nm 個あるどの変数でもガーベッジコレクトできるようにします。 | と定義します。3SATに出現する変数に対応する真偽値設定用の要素は 2nm 個あります。そのうち、真偽値設定モジュールで半数を利用するので、残りは nm 個です。そのうち、充足性判定用に各節から 1 つずつ、合計 m 個の要素を使います。残った m(n−1) 個をガーベッジコレクションするので、 g<sub>1</sub>[k], g<sub>2</sub>[k]を 1 ≤ k ≤ m(n−1) 個用意し、それぞれについて、nm 個あるどの変数でもガーベッジコレクトできるようにします。 | ||
| − | ; | + | ===3SAT→3DMの例=== |
3SAT 問題 (x ∨ y ∨ z) ∧ (¬ x ∨ ¬y ∨ z) を変換します。変数は x, y, z 、節の数は2つなので以下の真偽値設定モジュールを用意します。赤く示してあるのは、¬x, y, z を T に設定する時に選択する三つ組で、それぞれ M<sub>x</sub><sup>F</sup>, M<sub>y</sub><sup>T</sup>, M<sub>z</sub><sup>T</sup> に対応します。 | 3SAT 問題 (x ∨ y ∨ z) ∧ (¬ x ∨ ¬y ∨ z) を変換します。変数は x, y, z 、節の数は2つなので以下の真偽値設定モジュールを用意します。赤く示してあるのは、¬x, y, z を T に設定する時に選択する三つ組で、それぞれ M<sub>x</sub><sup>F</sup>, M<sub>y</sub><sup>T</sup>, M<sub>z</sub><sup>T</sup> に対応します。 | ||
| Line 128: | Line 128: | ||
まとめると、m 節 n 変数の 3SAT 問題は、2mn + 3m + 2mn × m(n−1) 組からなる 3DM 問題に変換されることがわかります。 | まとめると、m 節 n 変数の 3SAT 問題は、2mn + 3m + 2mn × m(n−1) 組からなる 3DM 問題に変換されることがわかります。 | ||
3SAT を充足可能とする変数のアサインメントに従えば 3DM の解を構成でき、逆に 3DM の解となる三つ組を選択すると、 3SAT を充足します。 | 3SAT を充足可能とする変数のアサインメントに従えば 3DM の解を構成でき、逆に 3DM の解となる三つ組を選択すると、 3SAT を充足します。 | ||
| + | |||
| + | ==二分割問題== | ||
| + | |||
| + | ;二分割 (partition) 問題 | ||
| + | 集合 A の各要素 a ∈ A に重さ s(a) ∈ Z<sup>+</sup> が定義されているとき、総重量がちょうど半分になる A の部分集合 A' ⊂ A が存在するか。 | ||
| + | |||
| + | <math>\textstyle\sum_{a \in A'} s(a) = \sum_{a \in A - A'} s(a)</math> | ||
| + | |||
| + | 集合 A の要素の総和 <math>\textstyle\sum_{a \in A} s(a)</math> が奇数だったら直ちに NO と言えますし、重さ順に並べてバランスをとればうまく解けそうな問題に見えますが、これから二分割問題で 3DM 問題を表現できる(部分問題として含む)ことを示します。 | ||
| + | |||
| + | W, X, Y のサイズが q, 三つ組の集合 M が要素を k 個含む 3DM 問題を考えます。まず M に含まれる各要素を 3q 桁からなる数字で表現します。要素を m = { w<sub>h</sub>, x<sub>i</sub>, y<sub>j</sub> } (1 ≤ h, i, j ≤ q) と書くと、この三つ組 m に対応する数字 f(m) は初めの q 桁のうち h 番目だけ 1 にして残りを 0、真ん中の q 桁のうち i 番目だけ 1 にして残りを 0、最後の q 桁のうち j 番目だけ 1 にして残りを 0 にしたものです。M の部分集合で 3DM を作れる場合、マッチングに対応する要素の数字を全部足し合わせた数は、3q 桁全てを 1 にした数に等しくなります。この、全桁が 1 である数を B とおきましょう。また全数字の和を <math>\textstyle\sum_{m \in M} f(m) = F</math> とおきます。 | ||
| + | |||
| + | 二分割問題で用いる集合は、M に含まれる各要素 m を数字に変換した f(m) の値 k 個と、f<sub>1</sub> = 2F - B, f<sub>2</sub> = F + B からなる k + 2 個で構成します。これらの数字を全て足し合わせた値は<math> f_1 + f_2 + \textstyle\sum_{m \in M} f(m) = 4 F</math> | ||
| + | ですから、M の部分集合を選んでちょうど二分割できた場合、その総和は 2F です。このとき、f<sub>1</sub>, f<sub>2</sub> の両方を含むことはできず、どちらか片方のみ含みます。そのとき、f<sub>1</sub> または f<sub>2</sub> 以外の要素の和はちょうど B になり、 3DM を構成しています。 | ||
| + | |||
| + | 数字への変換手続きは 3DM の問題サイズに比例する時間で可能です。また M の大きさが k の場合、例えば W の要素 w<sub>i</sub> が最大 k 回現れる可能性があるため、数字に変換するときに (k+1) 進数を用います。そうすると総和である F を計算するときに桁の繰り上げが起きないので要素間で個数が影響することがありません。 | ||
| + | |||
| + | まとめると、W, X, Y のサイズが q、三つ組が k 個ある 3DM 問題が与えられたら、(k+1)進数で表現した 3q 桁の数字 k + 2 個を用いた二分割問題に変換することができました。 | ||
Revision as of 20:32, 12 October 2011
Contents |
問題の変換
SAT問題がNP完全であることが証明されれば、他のNP完全問題をみつけることは楽になります。 ある問題がNP完全であることを示すには
- クラス NP に属する
- その問題がNP完全の問題を部分問題として含んでいる
ことを示せばよいだけです。
ここでは、3SAT → 3DM → Partition という順番で二つのNP完全問題を紹介します。
三次元マッチング
三次元マッチング (3-dimensional matching; 3DM) は、マッチング問題(または結婚問題)と呼ばれる有名な組み合わせ問題の三次元版です。
問題: サイズのひとしい集合 W, X, Y から一つずつ要素を取り出して作った三つ組の集合 E ⊆ W × X × Y が与えられた時、Eの中から |W| 組を取り出して、W, X, Y のいずれの要素も取りこぼしや重複なく選ぶことができるか。
例: W = { A, B, C }; X = { a, b, c }; Y = { 1, 2, 3 };
- E = (A, a, 1), (A, a, 3), (B, a, 1), (B, a, 3), (B, b, 1), (B, c, 2), (C, c, 2)
この問題の解は (A, b, 1) (B, a, 3) (C, c, 2) で、W, X, Y の要素がそれぞれ1度ずつ使われています。
- 定理:3DM はNP完全問題
正解となる組を与えられたら、集合 W, X, Y の要素が全て重複なく使われているかどうかはすぐに判定できるので 3DM ∈ NP です。 これから 3SAT問題を3DM問題に変換しましょう。3SAT問題は変数 { u1, u2, ... , un } を用いた節集合 C = { c1, c2, ... , cm } で構成されるとします。
三つ組の集合 M は、真偽値の設定用、充足性判定用、ガーベッジコレクション用の 3 タイプ用意します。
- 真偽値の設定用
3SATに登場する各変数 u に対し、節の数 m 個に対応する以下のマッチングモジュール M を用意します。
MuT = { (¬u[k], a[k], b[k]): 1 ≤ k ≤ m }
MuF = { (u[k], a[k+1], b[k]): 1 ≤ k < m } ∪ { u[m], a[1], b[m] }
ここで変数 a, b は変数 u を3DMに変換するために用いるもので、各 u の変換にしか登場しません。 このユニットをみたすマッチングは、MT に対応する m 個の三つ組を選択するか、MF に対応する m 個を選択するかしかありません。つまり、変数 u を T か F のどちらかに設定できます。3SATを充足するアサインメントで変数 u が T のとき、MT の三つ組 ( m 個) を選択します。変数 u が F のときは MF を選択します。
- 充足性判定用
充足性判定用のマッチングモジュールは、m 個ある各節 c 毎に用意します。節 c に出てくる変数が (ui, uj, uk) だとすると
Mc: { ui, s1, s2 } ∪ { uj, s1, s2 } ∪ { uk, s1, s2 }
を用意します。(もし節の中で ¬ui という使われ方をしていたら、{ ¬ui, s1, s2 } という組をつくります。)ここでs1, s2は変換用の変数で、節 c を特定するために用います。各節を充足するには T となる要素が必ず一つは存在するので、その要素が s1, s2 とマッチングするように三つ組を選びます。
- ガーベッジコレクション用
充足性判定の部分では、各節において一つだけ T とする変数を選んでおり、残りを使いません。充足に使われなかった残りのリテラルは、ガーベッジコレクション用の三つ組で利用します。 ガーベッジコレクションの三つ組は専用の変数 g1, g2 を用いて
Gk: { (u[j], g1[k], g2[k]), (¬u[j], g1[k], g2[k]): 1 ≤ j ≤ m, 1 ≤ k ≤ m(n−1) }
と定義します。3SATに出現する変数に対応する真偽値設定用の要素は 2nm 個あります。そのうち、真偽値設定モジュールで半数を利用するので、残りは nm 個です。そのうち、充足性判定用に各節から 1 つずつ、合計 m 個の要素を使います。残った m(n−1) 個をガーベッジコレクションするので、 g1[k], g2[k]を 1 ≤ k ≤ m(n−1) 個用意し、それぞれについて、nm 個あるどの変数でもガーベッジコレクトできるようにします。
3SAT→3DMの例
3SAT 問題 (x ∨ y ∨ z) ∧ (¬ x ∨ ¬y ∨ z) を変換します。変数は x, y, z 、節の数は2つなので以下の真偽値設定モジュールを用意します。赤く示してあるのは、¬x, y, z を T に設定する時に選択する三つ組で、それぞれ MxF, MyT, MzT に対応します。
| 変数 x: | (x[1], b[1], a[2]) | (¬x[1], a[1], b[1]) | (x[2], b[2], a[1]) | (¬x[2], a[2], b[2]) |
| 変数 y: | (¬y[1], c[1], d[1]) | (y[1], d[1], c[2]) | (¬y[2], c[2], d[2]) | (y[2], d[2], c[1]) |
| 変数 z: | (¬z[1], e[1], f[1]) | (z[1], f[1], e[2]) | (¬z[2], e[2], f[2]) | (z[2], f[2], e[1]) |
また二つの節に対応する充足判定モジュールを用意します。ここでは ¬x, y を T とするので赤字で示した三つ組を選択します。(他の選択方法もあります。)
| Mc1: | (x[1], s1, s2) | (y[1], s1, s2) | (z[1], s1, s2) |
| Mc2: | (¬x[2], t1, t2) | (y[2], t1, t2) | (z[2], t1, t2) |
最後に、節を T にするのに利用しなかった要素 x[1], y[2], z[1], z[2] がマッチングから外れているのでこれらをガーベッジコレクションします。
| G1: | (x[1], g1[1], g2[1]) | (¬x[1], g1[1], g2[1]) | (x[2], g1[1], g2[1]) | (¬x[2], g1[1], g2[1]) |
|---|---|---|---|---|
| (y[1], g1[1], g2[1]) | (¬y[1], g1[1], g2[1]) | (y[2], g1[1], g2[1]) | (¬y[2], g1[1], g2[1]) | |
| (z[1], g1[1], g2[1]) | (¬z[1], g1[1], g2[1]) | (z[2], g1[1], g2[1]) | (¬z[2], g1[1], g2[1]) | |
| G2: | (x[1], g1[2], g2[2]) | (¬x[1], g1[2], g2[2]) | (x[2], g1[2], g2[2]) | (¬x[2], g1[2], g2[2]) |
| (y[1], g1[2], g2[2]) | (¬y[1], g1[2], g2[2]) | (y[2], g1[2], g2[2]) | (¬y[2], g1[2], g2[2]) | |
| (z[1], g1[2], g2[2]) | (¬z[1], g1[2], g2[2]) | (z[2], g1[2], g2[2]) | (¬z[2], g1[2], g2[2]) | |
| G3: | (x[1], g1[3], g2[3]) | (¬x[1], g1[3], g2[3]) | (x[2], g1[3], g2[3]) | (¬x[2], g1[3], g2[3]) |
| (y[1], g1[3], g2[3]) | (¬y[1], g1[3], g2[3]) | (y[2], g1[3], g2[3]) | (¬y[2], g1[3], g2[3]) | |
| (z[1], g1[3], g2[3]) | (¬z[1], g1[3], g2[3]) | (z[2], g1[3], g2[3]) | (¬z[2], g1[3], g2[3]) | |
| Gm(n−1) | (x[1], g1[4], g2[4]) | (¬x[1], g1[4], g2[4]) | (x[2], g1[4], g2[4]) | (¬x[2], g1[4], g2[4]) |
| (y[1], g1[4], g2[4]) | (¬y[1], g1[4], g2[4]) | (y[2], g1[4], g2[4]) | (¬y[2], g1[4], g2[4]) | |
| (z[1], g1[4], g2[4]) | (¬z[1], g1[4], g2[4]) | (z[2], g1[4], g2[4]) | (¬z[2], g1[4], g2[4]) |
まとめると、m 節 n 変数の 3SAT 問題は、2mn + 3m + 2mn × m(n−1) 組からなる 3DM 問題に変換されることがわかります。 3SAT を充足可能とする変数のアサインメントに従えば 3DM の解を構成でき、逆に 3DM の解となる三つ組を選択すると、 3SAT を充足します。
二分割問題
- 二分割 (partition) 問題
集合 A の各要素 a ∈ A に重さ s(a) ∈ Z+ が定義されているとき、総重量がちょうど半分になる A の部分集合 A' ⊂ A が存在するか。
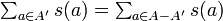
集合 A の要素の総和 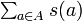 が奇数だったら直ちに NO と言えますし、重さ順に並べてバランスをとればうまく解けそうな問題に見えますが、これから二分割問題で 3DM 問題を表現できる(部分問題として含む)ことを示します。
が奇数だったら直ちに NO と言えますし、重さ順に並べてバランスをとればうまく解けそうな問題に見えますが、これから二分割問題で 3DM 問題を表現できる(部分問題として含む)ことを示します。
W, X, Y のサイズが q, 三つ組の集合 M が要素を k 個含む 3DM 問題を考えます。まず M に含まれる各要素を 3q 桁からなる数字で表現します。要素を m = { wh, xi, yj } (1 ≤ h, i, j ≤ q) と書くと、この三つ組 m に対応する数字 f(m) は初めの q 桁のうち h 番目だけ 1 にして残りを 0、真ん中の q 桁のうち i 番目だけ 1 にして残りを 0、最後の q 桁のうち j 番目だけ 1 にして残りを 0 にしたものです。M の部分集合で 3DM を作れる場合、マッチングに対応する要素の数字を全部足し合わせた数は、3q 桁全てを 1 にした数に等しくなります。この、全桁が 1 である数を B とおきましょう。また全数字の和を 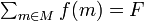 とおきます。
とおきます。
二分割問題で用いる集合は、M に含まれる各要素 m を数字に変換した f(m) の値 k 個と、f1 = 2F - B, f2 = F + B からなる k + 2 個で構成します。これらの数字を全て足し合わせた値は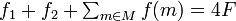 ですから、M の部分集合を選んでちょうど二分割できた場合、その総和は 2F です。このとき、f1, f2 の両方を含むことはできず、どちらか片方のみ含みます。そのとき、f1 または f2 以外の要素の和はちょうど B になり、 3DM を構成しています。
ですから、M の部分集合を選んでちょうど二分割できた場合、その総和は 2F です。このとき、f1, f2 の両方を含むことはできず、どちらか片方のみ含みます。そのとき、f1 または f2 以外の要素の和はちょうど B になり、 3DM を構成しています。
数字への変換手続きは 3DM の問題サイズに比例する時間で可能です。また M の大きさが k の場合、例えば W の要素 wi が最大 k 回現れる可能性があるため、数字に変換するときに (k+1) 進数を用います。そうすると総和である F を計算するときに桁の繰り上げが起きないので要素間で個数が影響することがありません。
まとめると、W, X, Y のサイズが q、三つ組が k 個ある 3DM 問題が与えられたら、(k+1)進数で表現した 3q 桁の数字 k + 2 個を用いた二分割問題に変換することができました。