Aritalab:Lecture/Algorithm/Halting Problem

問題を解くということ

チューリング機械（＝プログラム）が "問題を解ける" ためには、全ての可能な入力に対して

• 必ず停止する（無限ループに陥らない）
• 必ず正しい答えをだす

ことが要求されます。例えば、階乗を計算するプログラムがあったとして、入力する値によって無限ループに陥ったり、計算結果が間違っている可能性があるとしたら、皆さんもプログラムは "バグがある" と思うでしょう。

チューリング機械が "解ける" 問題の範囲とはどのようなものでしょう。

停止性問題

チューリング機械（＝プログラム） T に任意の入力 x を入れたとき有限時間で停止するか、を判定する問題を停止性問題といいます。この問題を解くプログラムは存在しない、つまり解くことができません。もし停止性を判定できる万能なチューリング機械が存在すると仮定すると、それが停止すると判定した時に限って停止しないチューリング機械を簡単に設計できてしまい、矛盾が生じます。

導かれる事例

• プログラムが無限ループを含むか判定できるコンパイラやデバッガは（理論的に）作れない
• いかなるアルゴリズム、プログラムをもってしても解けない問題が存在する

矛盾の導き方

任意のプログラム P と入力 x を受け取って、P が止まるか否かを有限時間で YES/NO と答えられるプログラム C(P, x) があると仮定します。（C をコンパイラと考えると分かりやすい。）C は必ず有限時間で止まり、C(P, P) という入力（つまりプログラム P 自身を数値に置き換えて入力にしてしまう）に対しても YES/NO と答えます。ここで、このコンパイラプログラム C に細工をして、C(P, P) が YES なら無限ループさせ（無限ループを付け加えるのは簡単）、C(P, P) が NO なら YES と出力して停止する C' を作成します。この新しいコンパイラ C' に C' 自身を数値に置き換えた値を入力するとどうなるでしょうか。

• C'(C', C') が停止する場合

C(C', C') が NO となるため、プログラム C' は 入力 C' に対して停止しないことになります。ですから、C'(C', C') が停止するのは矛盾です。

• C'(C', C') が停止しない場合

C(C', C') が YES となるため、プログラム C' は入力 C' に対して停止しなくてはなりません。やはり矛盾になります。

ポストの対応問題

無限ループを含むか否かをあらゆるプログラムについて判定できるという停止性問題は、直感的にも大変難しいように思えます。しかし、以下に述べる簡単な問題が、少なくとも停止性問題と同等に難しいことを示せます。

ポストの対応問題

あるアルファベット Σ からなる語 k 対 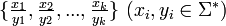$\textstyle \{ \frac{x_1}{y_1}, \frac{x_2}{y_2}, ... , \frac{x_k}{y_k} \} \ (x_i, y_i \in \Sigma^*)$ に対し、重複を許して並べることで上側と下側に同じ文字列 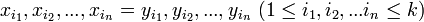$x_{i_1}, x_{i_2}, ... , x_{i_n} = y_{i_1}, y_{i_2}, ... , y_{i_n} \ (1 \leq i_1, i_2, ... i_n \leq k)$ を作れるか。

例

{ 0, 1 } ∈ Σ 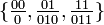$\textstyle \{ \frac{00}{0}, \frac{01}{010}, \frac{11}{011} \}$ は解をもつか。

解は存在し、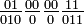$\textstyle \frac{01}{010} \frac{00}{0} \frac{00}{0} \frac{11}{011}$

例

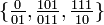{ 0, 1 } ∈ Σ $\textstyle \{ \frac{0}{01}, \frac{101}{011}, \frac{111}{10} \}$ は解をもつか。

解は存在しない

この問題を解くアルゴリズムは存在しません。つまり、どのようなリスト対を与えられても解があるなら YES と答えられるプログラムは存在しません。もし存在すると仮定すると、 停止性問題が解けてしまうことを利用します。

停止性問題の変換

チューリングマシン T が入力 x を受理する際の様相の列 (q₀, ε, x) ⇒...⇒ (q_f, y, z) が存在するときに限って、その列を解に持つような対応問題を構成できることを示します。それには、マシン T の状態遷移関数を表現する記号対を作れば十分です。

状態遷移関数は有限個用意され、 δ: (Q - {q_Y, q_N}) × Γ → Q × Γ × {−1, +1} と書けます（チューリングマシン参照)。まず、初期状態およびヘッドが左に動く場合と右に動く場合に対応する対を作成します。

• 初期状態 q₀ で入力 a₁a₂ ... a_n がある場合は $\textstyle\frac{\#}{\#q_0 a_1 a_2 ... a_n \#}$

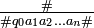
ここで # は様相を区切る記号です。q₀ という状態記号でヘッドの位置を示しており、ヘッドの右側に入力 a₁ ... a_n があることを示しています。

• δ(q, x) = (r, y, +1) の場合は 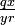$\textstyle\frac{qx}{yr}$ (x, y ∈ Γ; q, r ∈ Q - {q_Y, q_N})

状態 q でヘッドの右側に記号 x があるとき、 x を y に上書きして状態 r に移動、ヘッドは右に移動して y の左側に来ることを意味しています。この対は、ヘッドを右に動かす遷移関数 1 個につき、1 個用意します。

• δ(q, x) = (r, y, −1) の場合は 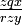$\textstyle\frac{zqx}{rzy}$ (x, y, z ∈ Γ; q, r ∈ Q - {q_Y, q_N})

状態 q でヘッドの左側に記号 z 右側に記号 x があるとき、 x を y に上書きして状態 r に移動、ヘッドは左に移動して z の左側に来ることを意味しています。記号 z は状態 q のとき、ヘッドの左側にあるテープ記号を意味します。よってヘッドを左に動かす遷移関数 1 個につき、 | Σ | 個用意しておきます。

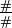さらに、ヘッド周辺以外のテープ内容を対応させる対として $\textstyle\frac{x}{x}$ (x ∈ Γ)、様相の区切りを表す対として $\textstyle\frac{\#}{\#}$ を、あわせて | Σ | + 1 個用意しておきます。

参考